MA9 Jakso 5: Todennäköisyyslaskenta
1. Kertausta
Murtoluvut
Murtolukujen yhteen- ja vähennyslaskussa murtolukujen tulee olla samannimisiä.
\(\mathsf{\dfrac{3}{8} + \dfrac{1}{8} = \dfrac{4}{8}^{(4} \!\!\!= \dfrac{1}{2}}\)
\(\mathsf{\dfrac{7}{9} - \!\!\!\rule{0pt}{1.2em}^{3)}\!\dfrac{1}{3} = \dfrac{7}{9} - \dfrac{3}{9} = \dfrac{4}{9}}\)
Murtolukujen kertolaskussa osoittajat ja nimittäjät kerrotaan keskenään.
\(\mathsf{\dfrac{3}{5} \cdot \dfrac{2}{7} = \dfrac{6}{35}}\)
Kokonaisluku voidaan ajatella murtolukuna, jolloin kertolasku kohdistuu osoittajaan.
\(\mathsf{\dfrac{2}{5} \cdot 15 = \dfrac{2 \cdot 15}{5} = \dfrac{30}{5} = 6}\)
Osan ottaminen luvusta lasketaan kertolaskun avulla.
Esimerkki: Kuinka paljon on kolme neljäsosaa luvusta 32?
\(\require{cancel}\mathsf{\dfrac{3}{4} \cdot 32 = \dfrac{3 \cdot \cancel{32}\!\!\!\!\!\rule{0pt}{1.3em}^8}{\cancel{4}} = 3 \cdot 8 = 24}\)
Murtoluvun käänteisluvussa osoittaja ja nimittäjä vaihtavat paikkaa.
Luku: \(\mathsf{\dfrac{3}{7}}\), Käänteisluku: \(\mathsf{\dfrac{7}{3}}\)
Käänteislukua voidaan merkitä murtolukuna \(\mathsf{\dfrac{1}{luku}}\) tai korotettuna negatiiviseen potenssiin \(\mathsf{\text{luku}^{-1}}\).
\(\mathsf{8^{-1} = \dfrac{1}{8}}\)
\(\mathsf{\left(\dfrac{3}{7}\right)^{-1} = \dfrac{1}{\frac{3}{7}} = \dfrac{7}{3}}\)
Prosenttilaskenta
Prosentti on on sadasosa.
\(\mathsf{1\:\% = \dfrac{1}{100} = \text{0,01}}\)
Prosenttiosuus saadaan jakamalla osa kokonaisuudella.
Esimerkki: Kuinka monta prosenttia 4 euroa on 15 eurosta?
\(\mathsf{\dfrac{4}{15} = \text{0,2666....} \approx 27\:\%}\)
Vastaus: 4 euroa on n. 27 prosenttia 15 eurosta.
Prosenttiosuuden ottaminen jostakin kokonaisuudesta lasketaan kertolaskun avulla. Prosenttiluku muutetaan desimaaliluvuksi (tai murtoluvuksi) ennen laskemista.
Esimerkki: Kuinka paljon on 16 prosenttia 450 ihmisestä?
\(\mathsf{16\:\% = \text{0,16}}\)
\(\mathsf{\text{0,16} \cdot 450 = 72}\)
Vastaus: 72 ihmistä on 16 prosenttia 450 ihmisestä.
Kokonaisuus saadaan laskettua jakamalla osa sitä vastaavalla prosenttiosuudella.
Esimerkki: Mistä matkasta 12 prosenttia on 720 metriä?
\(\mathsf{12\:\% = \text{0,12}}\)
\(\mathsf{\dfrac{720}{\text{0,12}} = 6000}\)
Vastaus: 720 metriä on 12 prosenttia 6 000 metristä.
Suuret ja pienet luvut
Laskimet antavat suuret ja pienet luvut kymmenpotenssin avulla. Luku saadaan siirtämällä pilkkua eksponentin osoittama määrä.
\(\mathsf{\text{3,04} \cdot 10^5 = 304\:000}\) (positiivinen eksponentti, pilkku siirtyy oikealle)
\(\mathsf{\text{3,04} \cdot 10^{-5} = \text{0,0000304}}\) (negatiivinen eksponentti, pilkku siirtyy vasemmalle)
2. Todennäköisyyslaskennan perusteet
Käsitteitä
Satunnaisilmiö on tilanne jossa tapahtuu jokin satunnainen tapahtuma tai suoritetaan arvonta jollakin välineellä. Kyseessä voi olla esimerkiksi kolikonheitto, nopanheitto tai lapun poimiminen hatusta silmät sidottuna.
Alkeistapaus on yksittäinen tulos, joka satunnaisilmiössä voidaan saavuttaa. Esimerkiksi kolikonheitossa kruuna, nopanheitossa silmäluku 4 tai hatusta vedettäessä Jaanan nimi.
Perusjoukko koostuu kaikista alkeistapauksista. Perusjoukkoja ovat esimerkiksi kolikonheitossa kruuna ja klaava, nopanheitossa silmäluvut 1, 2, 3, 4, 5 ja 6 tai hatussa olevat nimilaput "Jaana", "Pekka", "Simo" ja "Reetta".
Tapahtuma tarkoittaa jonkin ehdon määrittämää joukkoa alkeistapauksia. Esimerkiksi nopanheitossa tapahtuma "Silmäluku on pienempi kuin 3" sisältää alkeistapaukset 1 ja 2.
Todennäköisyys on jonkin tapahtuman alkeistapausten lukumäärän suhde perusjoukon alkeistapausten lukumäärään. Jonkin tapahtuman todennäköisyyttä merkitään isolla kirjaimella \(\mathsf{P}\) (engl. probability), jonka jälkeen tulee lyhyt kuvaus tapahtumasta sulkeiden sisään kirjoitettuna, esimerkiksi \(\textsf{P(kruuna)}\), \(\textsf{P(pienempi kuin 3)}\) tai \(\textsf{P(Jaana)}\).
Todennäköisyys voidaan ilmoittaa prosenttilukuna, murtolukuna tai desimaalilukuna. Mitä suurempi todennäköisyys on, sitä varmemmin tapahtuma tapahtuu. Jos todennäköisyys on 100 %, tapahtuma tapahtuu varmasti. Jos todennäköisyys on 0 %, tapahtuma ei tapahdu lainkaan. Jos todennäköisyys on suurempi kuin 50 %, niin tapahtuma tapahtuu ennemin kuin jää tapahtumatta.
Tapahtuman todennäköisyys:
\(\mathsf{\text{P(tapahtuma)} = \dfrac{\text{Suotuisat alkeistapaukset}}{\text{Kaikki alkeistapaukset}}}\)
Klassinen todennäköisyys
Jos satunnaisilmiön perusjoukon alkeistapaukset ovat symmetriset eli yhtä todennäköiset, voidaan tapahtumalle laskea klassinen todennäköisyys. Tarkasteltavan tapahtuman alkeispatauksia voidaan kutsua myös suotuisiksi alkeistapauksiksi.
Tapahtuman todennäköisyys:
\(\mathsf{\text{P(tapahtuma)} = \dfrac{\text{Suotuisat alkeistapaukset}}{\text{Kaikki alkeistapaukset}}}\)
Esimerkki: Pussissa on 5 sinistä (S), 3 punaista (P) ja 2 vihreää (V) palloa. Millä todennäköisyydellä pussista satunnaisesti nostettu pallo on punainen?
Kaikki alkeistapaukset (perusjoukko): S, S, S, S, S, P, P, P, V ja V, eli 10 vaihtoehtoa.
Suotuisat alkeistapaukset: P, P ja P, eli 3 vaihtoehtoa.
Todennäköisyys:
\(\mathsf{P(\text{punainen}) = \dfrac{3}{10} = \text{0,3} = 30\:\%}\)
Vastaus: Pallo on 30 prosentin todennäköisyydellä punainen.
Kertolaskusääntö ja yhteenlaskusääntö
Tarkastellaan kahta todennäköisyyttä \(\mathsf{P(A)}\) ja \(\mathsf{P(B)}\). Jos halutaan, että molemmat tapahtuvat, todennäköisyydet kerrotaan keskenään.
\(\mathsf{P(\text{A ja B}) = P(A) \cdot P(B)}\)
Jos halutaan, että ainakin toinen tapahtuu, todennäköisyydet lasketaan yhteen ja niistä vähennetään tilanne, jossa molemmat tapahtuvat.
\(\mathsf{P(\text{A tai B}) = P(A) + P(B) - P(\text{A ja B})}\)
Esimerkki: Jounilla on laukussaan kuusi paitaa ja kolmet housut. Paidoista kolme on keltaista, kaksi mustaa ja yksi punainen. Housuista kahdet ovat mustat ja yhdet siniset.
Millä todennäköisyydellä satunnaisesti valitaan
a) musta paita (mP) ja mustat housut (mH)
Käytetään kertolaskusääntöä:
\(\begin{align}&\mathsf{P(\text{musta paita ja mustat housut})}\\ &= \mathsf{P(\text{musta paita}) \cdot P(\text{mustat housut})}\\ &= \mathsf{\dfrac{2}{6} \cdot \dfrac{2}{3}}\\ &= \mathsf{\dfrac{4}{18}}\\ &= \mathsf{\text{0,222...}}\\ &\approx \mathsf{22\:\%}\end{align}\)
\(\begin{align}&\mathsf{P(\text{mP ja mH})}\\ &= \mathsf{P(\text{mP}) \cdot P(\text{mH})}\\ &= \mathsf{\dfrac{2}{6} \cdot \dfrac{2}{3}}\\ &= \mathsf{\dfrac{4}{18}}\\ &= \textsf{0,222...}\\ &\approx\mathsf{22\:\%}\end{align}\)
Vastaus: Musta paita ja housut valitaan 22 prosentin todennäköisyydellä.
b) musta paita (mP) tai mustat housut (mH)?
Käytetään yhteenlaskusääntöä:
\(\begin{align}&\mathsf{P(\text{musta paita tai mustat housut})}\\ &= \mathsf{P(\text{musta paita}) + P(\text{mustat housut}) - P(\text{musta paita ja mustat housut})}\\ &= \mathsf{\dfrac{2}{6} + \dfrac{2}{3} - \dfrac{4}{18}}\\ &= \mathsf{\text{0,777...}}\\ &\approx \mathsf{78\:\%}\end{align}\)
\(\begin{align}&\textsf{P(mP tai mH)}\\ &= \mathsf{P(\text{mP}) + P(\text{mH}) - P(\text{mP ja mH})}\\ &= \mathsf{\dfrac{2}{6} + \dfrac{2}{3} - \dfrac{4}{18}}\\ &= \mathsf{\text{0,777...}}\\ &\approx \mathsf{78\:\%}\end{align}\)
Vastaus: Musta paita tai mustat housut valitaan 78 prosentin todennäköisyydellä.
Vastatapahtuma
Vastatapahtuma (komplementtitapahtuma) tarkoittaa tilannetta, missä tarkasteltava tapahtuma ei tapahdu. Vastatapahtuman todennäköisyys voidaan laskea vähentämällä tapahtuman todennäköisyys 100 prosentista eli luvusta 1.
\(\mathsf{P(\text{A ei tapahdu}) = 1 - P(\text{A tapahtuu})}\)
Ongelman ratkaisemista vastatapahtuman avulla voi käyttää esimerkiksi silloin, kun ehto tapahtuman todennäköisyydelle on määritetty muodossa "muu kuin A", "ainakin yksi" tai kun sen vastatapahtuman todennäköisyys tunnetaan ennalta.
Esimerkki: Ulrikan penaalissa on kolme lyijykynää, kaksi mustekynää ja neljä tussia. Millä todennäköisyydellä satunnaisesti penaalista valittu kynä on muu kuin tussi?
Ratkaistaan tehtävä vastatapahtuman avulla.
\(\mathsf{P(\text{ei tussi}) = 1 - P(\text{tussi}) = 1 - \dfrac{4}{9} = \dfrac{9}{9} - \dfrac{4}{9} = \dfrac{5}{9} = \text{0,555...} \approx 56\:\%}\)
\(\begin{align}&\mathsf{P(\text{ei tussi})}\\ &= \mathsf{1 - P(\text{tussi})}\\ &= \mathsf{1 - \dfrac{4}{9}}\\ &= \mathsf{\dfrac{9}{9} - \dfrac{4}{9}}\\ &= \mathsf{\dfrac{5}{9}}\\ &= \textsf{0,555...}\\ &\approx \mathsf{56\:\%}\end{align}\)
Vastaus: Kynä on 56 prosentin todennäköisyydellä muu kuin tussi.
Tilastollinen todennäköisyys
Jos alkeistapausten todennäköisyyttä ei voida ennalta tietää, voidaan kerätä tilasto tai suorittaa toistokoe, jonka avulla määritetään tapauksille tilastollinen todennäköisyys. Tilastollinen todennäköisyys on aina likiarvo ja sen tarkkuus paranee mitä useamman kerran koetta toistetaan tai mitä suurempi otos tilastoon kerätään.
Esimerkki: Millä todennäköisyydellä tiellä vastaan tuleva ajoneuvo on mopo?
| Ajoneuvo | Lukumäärä |
|---|---|
| Henkilöautot | 3 699 634 |
| Pakettiautot | 524 672 |
| Kuorma-autot | 173 769 |
| Linja-autot | 19 649 |
| Moottoripyörät | 239 872 |
| Kevytmoottoripyörät | 52 373 |
| Mopot | 363 455 |
| Mopoautot | 12 777 |
| Muut kolmi- ja nelipyörät | 20 459 |
| Moottorityökoneet ja traktorit | 572 276 |
| Yhteensä | 5 678 936 |
Rekisterissä olleiden ajoneuvojen lukumäärä 31.12.2022 (ml. Ahvenanmaa)
Lähde: stat.fi
\(\mathsf{P(\text{mopo}) = \dfrac{363\:455}{5\:678\:936} = \text{0,0640...} \approx \text{6,4 %}}\)
Vastaus: Mopo tulee vastaan 6,4 prosentin todennäköisyydellä.
Vaihtoehtojen lukumäärä
Ennen todennäköisyyden laskemista tulee tuntea kaikkien mahdollisten alkeistapausten lukumäärä sekä suotuisten alkeistapausten lukumäärä. Kaikki erilaiset vaihtoehdot voidaan saada selville esimerkiksi luettelemalla, piirtämällä valintapuu tai laskemalla. Yksittäisen tapahtuman vaihtoehtojen lukumäärä on helppo laskea, jos kyseessä on jokin järkevän kokoinen kohde, esimerkiksi kolikko, noppa, korttipakka, luokan oppilaat, kirjaimet, numerot, tms. Jos tarkastellaan perättäisiä tapahtumia, vaihtoehtojen lukumäärä saadaan kertomalla eri vaiheissa olevien tapahtumien vaihtoehtojen lukumäärät keskenään. Tätä kutsutaan tuloperiaatteeksi.
Toisistaan riippumattomat tapahtumat
Jos edellisen tapahtuman tulos ei vaikuta seuraavien tapahtumien lukumääriin, ovat tapahtumat toisistaan riippumattomia.
Esimerkki: Käytettävissä on vihreää (V), oranssia (O) ja lilaa (L) lahjapaperia sekä sinistä (S), kultaista (K), punaista (P) ja hopeista (H) lahjanauhaa. Kuinka monta erilaista yhdistelmää lahjapakettiin voidaan valita.
Kaikkien vaihtoehtojen luetteleminen:
| VS | VK | VP | VH |
| OS | OK | OP | OH |
| LS | LK | LP | LH |
Valintapuu:
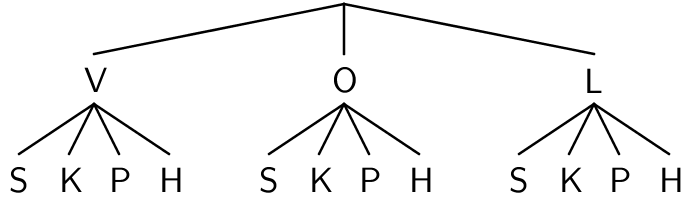
Laskeminen tuloperiaatteen avulla: 3 paperia ja 4 nauhaa.
\(\mathsf{3 \cdot 4 = 12}\)
Vastaus: Lahjapakettiin voidaan valita 12 erilaista yhdistelmää.
Toisistaan riippuvat tapahtumat
Jos edellisen tapahtuman tulos muuttaa seuraavien tapahtumien vaihtoehtojen lukumääriä, ovat tapahtumat toisistaan riippuvia.
Esimerkki: Neljä lasta saavat virvottuaan valita pussista tikkarin. Pussissa on neljä tikkaria, ja ne ovat kaikki eri värisiä: punainen (P), keltainen (K), vihreä (V) ja sininen (S). Kuinka monella eri tavalla tikkarit voidaan valita.
Kaikkien vaihtoehtojen luetteleminen:
| PKVS | PKSV | PVKS | PVSK | PSKV | PSVK |
| KPVS | KPSV | KVPS | KVSP | KSPV | KSVP |
| VPKS | VPSK | VKPS | VKSP | VSPK | VSKP |
| SPKV | SPVK | SKPV | SKVP | SVPK | SVKP |
Valintapuu:
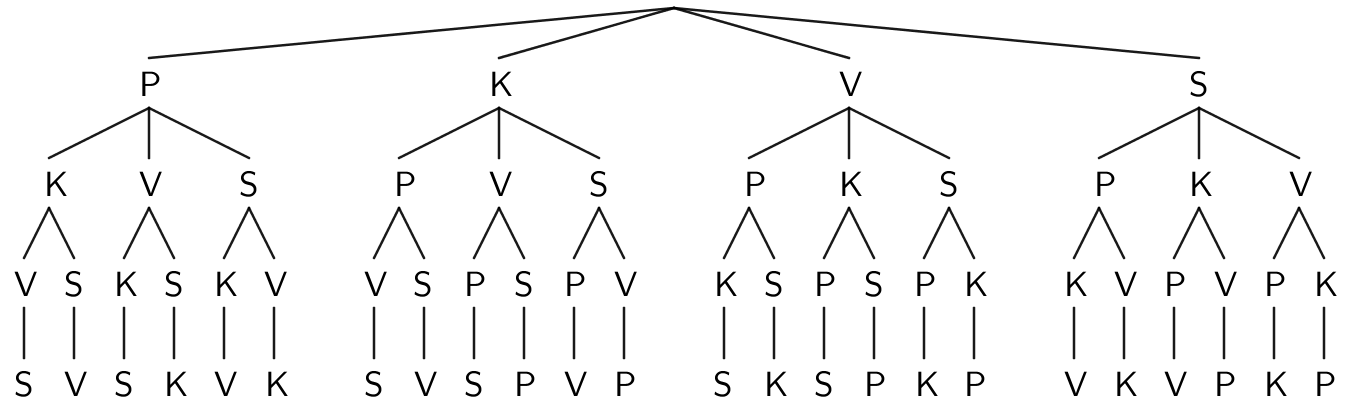
Laskeminen tuloperiaatteen avulla:
Ensimmäinen lapsi valitsee neljästä tikkarista, toinen kolmesta tikkarista, kolmas valitsee kahdesta tikkarista ja neljännellä lapsella on jäljellä enää yksi tikkari.
\(\mathsf{4 \cdot 3 \cdot 2 \cdot 1 = 24}\)
Vastaus: Tikkarit voidaan valita 24 erilaisella tavalla.
Valitaan vain osa, järjestyksellä on väliä
Valitaan jostakin joukosta vain tietty määrä yksilöitä ja asetetaan ne järjestykseen. Erilaisten järjestysten lukumäärä saadaan kertomalla jäljellä olevien yksilöiden määrällä kussakin valinnan vaiheessa.
Esimerkki: Koulun hiihtokilpailussa on 5 osallistujaa: Aada, Ben, Cecilia, Doris ja Eetu. Kuinka monella eri tavalla kulta- ja hopeamitalit voidaan jakaa?
Kaikkien vaihtoehtojen luetteleminen:
Ristiintaulukointi
| HOPEAMITALI | ||||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | ||
KULTAMITALI |
A | AB | AC | AD | AE | |
| B | BA | BC | BD | BE | ||
| C | CA | CB | CD | CE | ||
| D | DA | DB | DC | DE | ||
| E | EA | EB | EC | ED | ||
Valintapuu:
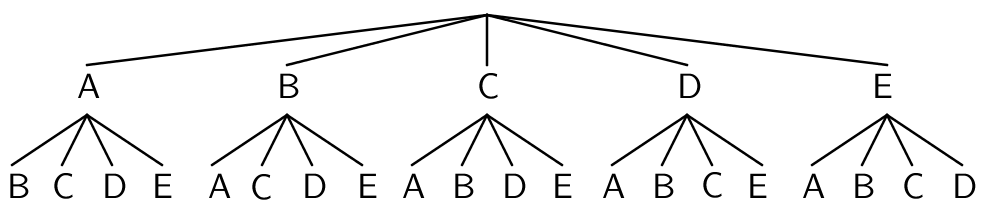
Laskeminen tuloperiaatteen avulla: Voittajaehdokkaita 5, jonka jälkeen hopealle voi päästä joku neljästä jäljelle jääneestä.
\(\mathsf{5 \cdot 4 = 20}\)
Vastaus: Kulta- ja hopeamitalit voidaan jakaa 20 eri tavalla.
Valitaan vain osa, järjestyksellä ei ole väliä
Valitaan jostakin joukosta vain tietty määrä yksilöitä. Yksilöiden järjestyksellä ei ole merkitystä. Lasketaan kertolasku kuten edellä, mutta jaetaan tulos samanlaisten valintojen lukumäärällä.
Esimerkki: Jääkiekkojoukkueeseen pyrkii kuusi maalivahtia, joista kolme valitaan lopulliseen joukkueeseen. Kuinka monella eri tavalla maalivahdit voidaan valita?
Kaikkien vaihtoehtojen luetteleminen: (maalivahdit A, B, C, D, E ja F)
| ABC | ABD | ABE | ABF | ACD |
| ACE | ACF | ADE | ADF | AEF |
| BCD | BCE | BCF | BDE | BDF |
| BEF | CDE | CDF | CEF | DEF |
Laskeminen:
Valitaan kolme maalivahtia järjestyksessä:
\(\mathsf{6 \cdot 5 \cdot 4 = 120}\)
Samat kolme maalivahtia esiintyvät useammassa eri valinnassa (esimerkiksi ABC, ACB, BAC, BCA, CAB, CBA).
\(\mathsf{3 \cdot 2 \cdot 1 = 6}\)
Jaetaan kaikkien vaihtoehtojen määrä samojen valintojen määrällä.
\(\mathsf{\dfrac{120}{6} = 20}\)
Vastaus: Maalivahdit voidaan valita 20 eri tavalla lopulliseen joukkueeseen.
Peräkkäiset tapahtumat
Kertolaskusääntö
Peräkkäisten tapahtumien todennäköisyys saadaan kertomalla todennäköisyydet keskenään.
Esimerkki: Pussissa on 5 palloa: 2 punaista ja 3 sinistä. Pussista nostetaan kaksi palloa. Millä todennäköisyydellä ensimmäisenä nostettu pallo on punainen ja toisena nostettu pallo sininen?
Ennen ensimmäistä nostoa pussissa on 2 punaista ja 3 sinistä palloa eli yhteensä 5 palloa:
\(\mathsf{P(\text{1. punainen}) = \dfrac{2}{5}}\)
Ennen toista nostoa pussissa on 1 punainen ja 3 sinistä palloa eli yhteensä 4 palloa:
\(\mathsf{P(\text{2. sininen}) = \dfrac{3}{4}}\)
Todennäköisyys, että molemmat tapahtuvat saadaan kertolaskulla:
\(\begin{align}&\mathsf{P(\text{1. punainen ja 2. sininen})}\\ &= \mathsf{P(\text{1. punainen}) \cdot P(\text{2. sininen})}\\ &= \mathsf{\dfrac{2}{5} \cdot \dfrac{3}{4}}\\ &= \mathsf{\dfrac{6}{20}}\\ &= \mathsf{\text{0,3}}\\ &= \mathsf{30\:\%}\end{align}\)
\(\begin{align}&\mathsf{P(\text{1. pun. ja 2. sin.})}\\ &= \mathsf{P(\text{1. pun.}) \cdot P(\text{2. sin.})}\\ &= \mathsf{\dfrac{2}{5} \cdot \dfrac{3}{4}}\\ &= \mathsf{\dfrac{6}{20}}\\ &= \mathsf{\text{0,3}}\\ &= \mathsf{30\:\%}\end{align}\)
Vastaus: Todennäköisyys, että ensimmäisellä nostolla tulee punainen ja toisella nostolla sininen pallo on 30 prosenttia.
Vaihtoehtoisesti voidaan laskea kaikkien tapausten ja suotuisten tapausten vaihtoehtojen lukumäärät perättäisistä tapahtumista, ja laskea todennäköisyys niiden avulla.
Esimerkki: Pussissa on 5 palloa: 2 punaista (P1 ja P2) ja 3 sinistä (S1, S2 ja S3). Pussista nostetaan kaksi palloa. Millä todennäköisyydellä ensimmäisenä nostettu pallo on punainen ja toisena nostettu pallo sininen?
Taulukoidaan kaikki alkeistapaukset. Samanväriset pallot on numeroitu alaindeksiin. Suotuisat alkeistapaukset on merkitty lihavoituna.
| P1P2 | P1S1 | P1S2 | P1S3 |
| P2P1 | P2S1 | P2S2 | P2S3 |
| S1P1 | S1P2 | S1S2 | S1S3 |
| S2P1 | S2P2 | S2S1 | S2S3 |
| S3P1 | S3P2 | S3S1 | S3S2 |
Todennäköisyys, että molemmat tapahtuvat saadaan laskemalla:
\(\mathsf{P(\text{1. punainen ja 2. sininen}) = \dfrac{suotuisat\,tapaukset}{kaikki\,tapaukset} = \dfrac{6}{20} = \text{0,3} = 30\:\%}\)
\(\begin{align}&\mathsf{P(\text{1. pun. ja 2. sin.})}\\ &= \mathsf{\dfrac{suotuisat\,tapaukset}{kaikki\,tapaukset}}\\ &= \mathsf{\dfrac{6}{20}}\\ &= \mathsf{\text{0,3}}\\ &= \mathsf{30\:\%}\end{align}\)
Vastaus: Todennäköisyys, että ensimmäisellä nostolla tulee punainen ja toisella nostolla sininen pallo on 30 prosenttia.
Yhteenlaskusääntö
Jos suotuisia tapahtumia on useita, todennäköisyydet lasketaan yhteen.
Esimerkki: Pussissa on 5 palloa: 2 punaista ja 3 sinistä. Pussista nostetaan kaksi palloa. Millä todennäköisyydellä pallot ovat eriväriset?
Suotuisa tapahtuma 1: 1. pallo on punainen ja 2. pallo on sininen:
\(\mathsf{P(\text{1. punainen ja 2. sininen}) = \dfrac{2}{5} \cdot \dfrac{3}{4} = \dfrac{6}{20}}\)
Suotuisa tapahtuma 2: 1. pallo on sininen ja 2. pallo on punainen:
\(\mathsf{P(\text{1. sininen ja 2. punainen}) = \dfrac{3}{5} \cdot \dfrac{2}{4} = \dfrac{6}{20}}\)
Todennäköisyys, että jompi kumpi tapahtuu, saadaan yhteenlaskulla:
\(\begin{align}&\mathsf{P(\text{eriväriset})}\\ &= \mathsf{P(\text{1. punainen ja 2. sininen}) + P(\text{1. sininen ja 2. punainen})}\\ &= \mathsf{\dfrac{6}{20} + \dfrac{6}{20}}\\ &= \mathsf{\dfrac{12}{20}}\\ &= \mathsf{\text{0,6}}\\ &= \mathsf{60\:\%}\end{align}\)
\(\begin{align}&\mathsf{P(\text{eriväriset})}\\ &= \mathsf{P(\text{1. pun. ja 2. sin.}) + P(\text{1. sin. ja 2. pun.})}\\ &= \mathsf{\dfrac{6}{20} + \dfrac{6}{20}}\\ &= \mathsf{\dfrac{12}{20}}\\ &= \mathsf{\text{0,6}}\\ &= \mathsf{60\:\%}\end{align}\)
Vastaus: Todennäköisyys, että pallot ovat erivärisiä on 60 prosenttia.
Vaihtoehtoisesti voidaan laskea kaikkien ja suotuisten vaihtoehtojen lukumäärät perättäisistä tapahtumista, ja laskea todennäköisyys niiden avulla.
Esimerkki: Pussissa on 5 palloa: 2 punaista (P1 ja P2) ja 3 sinistä (S1, S2 ja S3). Pussista nostetaan kaksi palloa. Millä todennäköisyydellä pallot ovat eriväriset?
Taulukoidaan kaikki alkeistapaukset. Samanväriset pallot on numeroitu alaindeksiin. Suotuisat alkeistapaukset on merkitty lihavoituna.
| P1P2 | P1S1 | P1S2 | P1S3 |
| P2P1 | P2S1 | P2S2 | P2S3 |
| S1P1 | S1P2 | S1S2 | S1S3 |
| S2P1 | S2P2 | S2S1 | S2S3 |
| S3P1 | S3P2 | S3S1 | S3S2 |
Lasketaan todennäköisyys:
\(\mathsf{P(\text{eriväriset}) = \dfrac{12}{20} = \text{0,6} = 60\:\%}\)
Vastaus: Todennäköisyys, että pallot ovat erivärisiä on 60 prosenttia.
3. Teemat
Todennäköisyyslaskentaa sovelletaan kaikenlaisten tieteiden lisäksi monilla arkielämän aloilla. Sen avulla voidaan simuloida ja ennustaa erilaisia tapahtumia. Monissa peleissä satunnaisuus ja sitä kautta erilaiset todennäköisyydet ovat suuressa roolissa pelin etenemisen kannalta. Uhkapeleissä (casinopelit, vedonlyönti) voittojen todennäköisyydet ja niistä laskettavat palautusprosentit määrittävät, kuinka nopeasti pelaaja häviää rahaa.
Palautusprosentti
Palautusprosentti kertoo kuinka paljon pelaaja keskimäärin panoksestaan saa takaisin yhdellä pelikierroksella. Jos palautusprosentti on pienempi kuin 100 % pelaaja häviää rahansa ajan kuluessa. Jos palautusprosentti on 90 %, niin jokaisella pelikierroksella saadaan 0,9 kertaisesti panostettu rahamäärä takaisin. Yhden euron panoksella hävitään joka kierroksella siis
\(\mathsf{\text{1,00 €} -\text{0,90 €} = \text{0,10 €}}\)
Jos alkupanostus on 10 euroa ja peliä pelataan 1 euron panoksella, pelikierroksia voidaan pelata keskimäärin
\(\mathsf{\dfrac{\text{10 €}}{\text{0,10 €}} = 100 \text{ kierrosta.}}\)
Missään rahapelissä ei palautusprosentti ole suurempi kuin 100 prosenttia. Mitä lähempänä se sataa prosenttia on, sitä pidempään peli voi jatkua. Pitkässä juoksussa rahat häviää kuitenkin varmasti.
Palautusprosentin laskeminen
Palautusprosentti voidaan laskea seuraavien vaiheiden kautta:
- Taulukoidaan kaikki erilaiset tapaukset, niiden palautuskertoimet ja todennäköisyydet.
- Lasketaan kullekkin tapaukselle voitto, joka saadaan vähentämällä panos kertoimesta.
- Kerrotaan voitto ja todennäköisyys keskenään.
- Lasketaan kertolaskujen tulokset yhteen.
- Lisätään (vähenetään) saatu prosenttiluku 100 prosentista.
Esimerkki: Laske pelin palautusprosentti, kun peliä pelataan yhden panoksella ja voitot sekä todennäköisyydet on ilmoitettu alla olevassa taulukossa.
| Tapahtuma | Kerroin | Voitto | Todennäköisyys |
|---|---|---|---|
| 3 oikein | 5 | 4 | \(\mathsf{7\:\%}\) |
| 2 oikein | 3 | 2 | \(\mathsf{10\:\%}\) |
| 1 oikein | 2 | 1 | \(\mathsf{12\:\%}\) |
| 0 oikein | 0 | -1 | \(\mathsf{71\:\%}\) |
Ratkaisu: Summataan riveittäin Voitto · Todennäköisyys
\(\mathsf{4 \cdot 7\:\% + 2 \cdot 10\:\% + 1 \cdot 12\:\% - 1 \cdot 71\:\% = 28\:\% + 20\:\% + 12\:\% - 71\:\% = -11\:\%}\)
\(\begin{align}&\mathsf{4 \cdot 7\:\% + 2 \cdot 10\:\% + 1 \cdot 12\:\% - 1 \cdot 71\:\%}\\ &= \mathsf{28\:\% + 20\:\% + 12\:\% - 71\:\%}\\ &= \mathsf{-11\:\%}\end{align}\)
\(\mathsf{100\:\% - 11\:\% = 89\:\%}\)
Vastaus: Pelin palautusprosentti on 89 prosenttia.
Kolikko
Kolikkoa käytetään päätöksenteon apuvälineenä mm. urheilussa, kun halutaan arpoa kahden vaihtoehdon välillä. Kolikossa on kaksi puolta: kuvapuoli eli kruuna (ruots. krona, eng. heads) ja arvopuoli klaava (ruots. klave, eng. tails).
Oletetaan, että kolikko kääntyy aina toiselle kyljelleen eikä voi jäädä pystyyn. Lisäksi oletetaan kolikon olevan symmetrinen sekä painottamaton, jolloin kruunan ja klaavan todennäköisyydet ovat
\(\mathsf{\dfrac{1}{2} = \text{0,5} = 50\:\%}\).
Esimerkki: Kolikkoa heitetään kaksi kertaa. Millä todennäköisyydellä saadaan kaksi kruunaa?
\(\mathsf{P(\text{2 kruunaa}) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4} = \text{0,25} = 25\:\%}\)
Vastaus: Kaksi kruunaa saadaan 25 prosentin todennäköisyydellä.
Esimerkki: Kolikkoa heitetään kaksi kertaa. Millä todennäköisyydellä saadaan vähintään yksi kruuna?
Tapa 1: Vastatodennäköisyys
\(\mathsf{P(\text{vähintään 1 kruuna}) = 1 - P(\text{ei yhtään kruunaa}) = 1 - \dfrac{1}{2} \cdot \dfrac{1}{2} = 1-\dfrac{1}{4} = \dfrac{3}{4} = \text{0,75} = 75\:\%}\)
\(\begin{align}&\mathsf{P(\text{vähintään 1 kruuna})}\\ &= \mathsf{1 - P(\text{ei yhtään kruunaa})}\\ &= \mathsf{1 - \dfrac{1}{2} \cdot \dfrac{1}{2}}\\ &= \mathsf{1-\dfrac{1}{4}}\\ &= \mathsf{\dfrac{3}{4}}\\ &= \textsf{0,75}\\ &= \mathsf{75\:\%}\end{align}\)
Tapa 2: Yhteenlaskuperiaate
\(\mathsf{P(\text{vähintään 1 kruuna}) = P(\text{1 kruuna}) + P(\text{kaksi kruunaa}) = \dfrac{1}{2} \cdot \dfrac{2}{2} + \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{2}{4} + \dfrac{1}{4} = \dfrac{3}{4} = \text{0,75} = 75\:\%}\)
\(\begin{align}&\mathsf{P(\text{vähintään 1 kruuna})}\\ &= \mathsf{P(\text{1 kruuna}) + P(\text{kaksi kruunaa})}\\ &= \mathsf{\dfrac{1}{2} \cdot \dfrac{2}{2} + \dfrac{1}{2} \cdot \dfrac{1}{2}}\\ &= \mathsf{\dfrac{2}{4} + \dfrac{1}{4}}\\ &= \mathsf{\dfrac{3}{4}}\\ &= \textsf{0,75}\\ &= \mathsf{75\:\%}\end{align}\)
Vastaus: Vähintään yksi kruuna saadaan 75 prosentin todennäköisyydellä.
Noppa
Noppaa käytetään arvontavälineenä esimerkiksi lautapeleissä tai erityisissä noppapeleissä. Yleisin noppamalli on kuusitahkoinen arpakuutio, jossa kuhunkin tahkoon on merkitty jokin silmäluku. Myös muun muotoisia säännöllisiä monitahokkaita käytetään noppina esimerkiksi roolipeleissä. Silmäluvut voivat olla myös muita kuin lukuja yhdestä alkaen.

Käsitellään jatkossa aina arpakuutiota, jollei toisin mainita. Oletetaan nopan olevan symmetrinen ja painottamaton, jolloin jonkin tietyn silmäluvun todennäköisyys on.
\(\mathsf{\dfrac{1}{6} = \text{0,16666...} \approx 17\:\%}\).
Esimerkki: Noppaa heitetään kerran. Millä todennäköisyydellä silmäluku on pariton (1, 3 tai 5).
\(\mathsf{P(\text{pariton}) = \dfrac{3}{6} = \text{0,5} = 50\:\%}\)
Vastaus: Pariton silmäluku saadaan 50 prosentin todennäköisyydellä.
Esimerkki: Noppaa heitetään kaksi kertaa. Millä todennäköisyydellä saadaan kaksi kuutosta?
\(\mathsf{P(\text{kaksi kuutosta}) = \dfrac{1}{6} \cdot \dfrac{1}{6} = \dfrac{1}{36} = \text{0,02777...} \approx \text{2,8}\:\%}\)
\(\begin{align}&\mathsf{P(\text{kaksi kuutosta})}\\ &= \mathsf{\dfrac{1}{6} \cdot \dfrac{1}{6}}\\ &= \mathsf{\dfrac{1}{36}}\\ &= \textsf{0,2777...}\\ &\approx \textsf{2,8 %}\end{align}\)
Vastaus: Kaksi kuutosta saadaan 2,8 prosentin todennäköisyydellä.
Esimerkki: Noppaa heitetään kaksi kertaa. Millä todennäköisyydellä silmäluvut eivät ole samat?
Erilaisia tapauksia yhteensä \(\mathsf{6 \cdot 6 = 36}\) kappaletta.
| 11, | 12, | 13, | 14, | 15, | 16, |
| 21, | 22, | 23, | 24, | 25, | 26, |
| 31, | 32, | 33, | 34, | 35, | 36, |
| 41, | 42, | 43, | 44, | 45, | 46, |
| 51, | 52, | 53, | 54, | 55, | 56, |
| 61, | 62, | 63, | 64, | 65, | 66 |
Suotuisia tapaksia (lihavoitu): 30
Todennäköisyys:
\(\mathsf{P(\text{eri luvut}) = \dfrac{30}{36} = \text{0,833...} \approx 83\:\%}\)
Vastaus: Silmäluvut eivät ole samoja 83 prosentin todennäköisyydellä.
Pelikortit
Pelikorttipakassa on 52 korttia. Pelikortit on jaettu kahteen väriin (punainen ja musta) sekä neljään maahan:
- hertta ♥
- ruutu ♦
- risti ♣
- pata ♠
Jokaisessa maassa on kolmetoista korttia, jotka on luokiteltu arvoin 1-13. Kirjaimella A (engl. ace, "ässä") kuvataan arvoa 1 (tai 14 joissakin korttipeleissä), kirjaimella J (engl. jack, "jätkä") arvoa 11, kirjaimella Q (engl. queen, "kuningatar", "akka", "rouva") arvoa 12 sekä kirjaimella K (engl. king, "kuningas", "kunkku", "kurko", "kalle") arvoa 13. Kortteja J, Q ja K kutsutaan kuvakorteiksi.
🂱🂲🂳🂴🂵🂶🂷🂸🂹🂺🂻🂽🂾
🃁🃂🃃🃄🃅🃆🃇🃈🃉🃊🃋🃍🃎
🃑🃒🃓🃔🃕🃖🃗🃘🃙🃚🃛🃝🃞
🂡🂢🂣🂤🂥🂦🂧🂨🂩🂪🂫🂭🂮
🂱🂲🂳🂴🂵🂶🂷🂸🂹🂺🂻🂽🂾
🃁🃂🃃🃄🃅🃆🃇🃈🃉🃊🃋🃍🃎
🃑🃒🃓🃔🃕🃖🃗🃘🃙🃚🃛🃝🃞
🂡🂢🂣🂤🂥🂦🂧🂨🂩🂪🂫🂭🂮
Joissakin korttipakoissa voi olla näiden 52 kortin lisäksi erikoiskortteja, esimerkiksi jokereita, joita voidaan käyttää tietyissä korttipeleissä. Käytetään jatkossa oletuksena 52 kortin pakkaa, ellei toisin mainita.
Esimerkki: Millä todennäköisyydellä satunnaisesti valittu pelikortti on
a) hertta 7
\(\mathsf{P(\text{hertta 7}) = \dfrac{1}{52} = \text{0,0192...} \approx \text{1,9}\:\%}\)
b) risti
\(\mathsf{P(\text{risti}) = \dfrac{13}{52} = \text{0,25} = 25\:\%}\)
c) kutonen
\(\mathsf{P(\text{kutonen}) = \dfrac{4}{52} = \text{0,0769...} \approx \text{7,7}\:\%}\)
d) punainen jätkä?
\(\mathsf{P(\text{punainen}) = \dfrac{26}{52} = \text{0,5} = 50\:\%}\)
Esimerkki: Ventissä on tavoitteena pakasta kortteja nostamalla saada korttien arvojen summa mahdollisimman lähelle lukua 21. Pelaaja voi valita onko ässä (A) arvoltaan 1 vai 14. Jos summa on suurempi kuin 21, pelaaja häviää. Jos pelin lopettaa summaan, joka on alle 21, voivat muut pelaajat ja jakaja yrittää päästä lähemmäksi lukua 21.
Henri on saanut kolmella ensimmäisellä nostolla seuraavat kortit.
🂵🃉🂢
Millä todennäköisyydellä Henrin korttien summa menee yli 21 seuraavalla nostolla?
Ratkaisu:
Summa nyt: \(\mathsf{5+9+2=16}\)
Pelin voittamiseen tarvittavan kortin arvo: \(\mathsf{21 - 16 = 5}\)
Todennäköisyys, että kortti on suurempi kuin 5:
\(\mathsf{P(>5) = \dfrac{31}{49} = \text{0,632...} = 63\:\%}\)
Vastaus: Seuraavalla nostolla on 63 prosentin todennäköisyys, että korttien summa menee yli luvun 21.
Ruletti
Ruletissa pelaaja pyrkii veikkaamaan lukua, johon rulettipyörässä oleva pallo pysähtyy. Pelaajalla on valittavanaan myös monenlaisia lukujen yhdistelmiä sekä punainen ja musta väri, joihin luvut on jaettu.
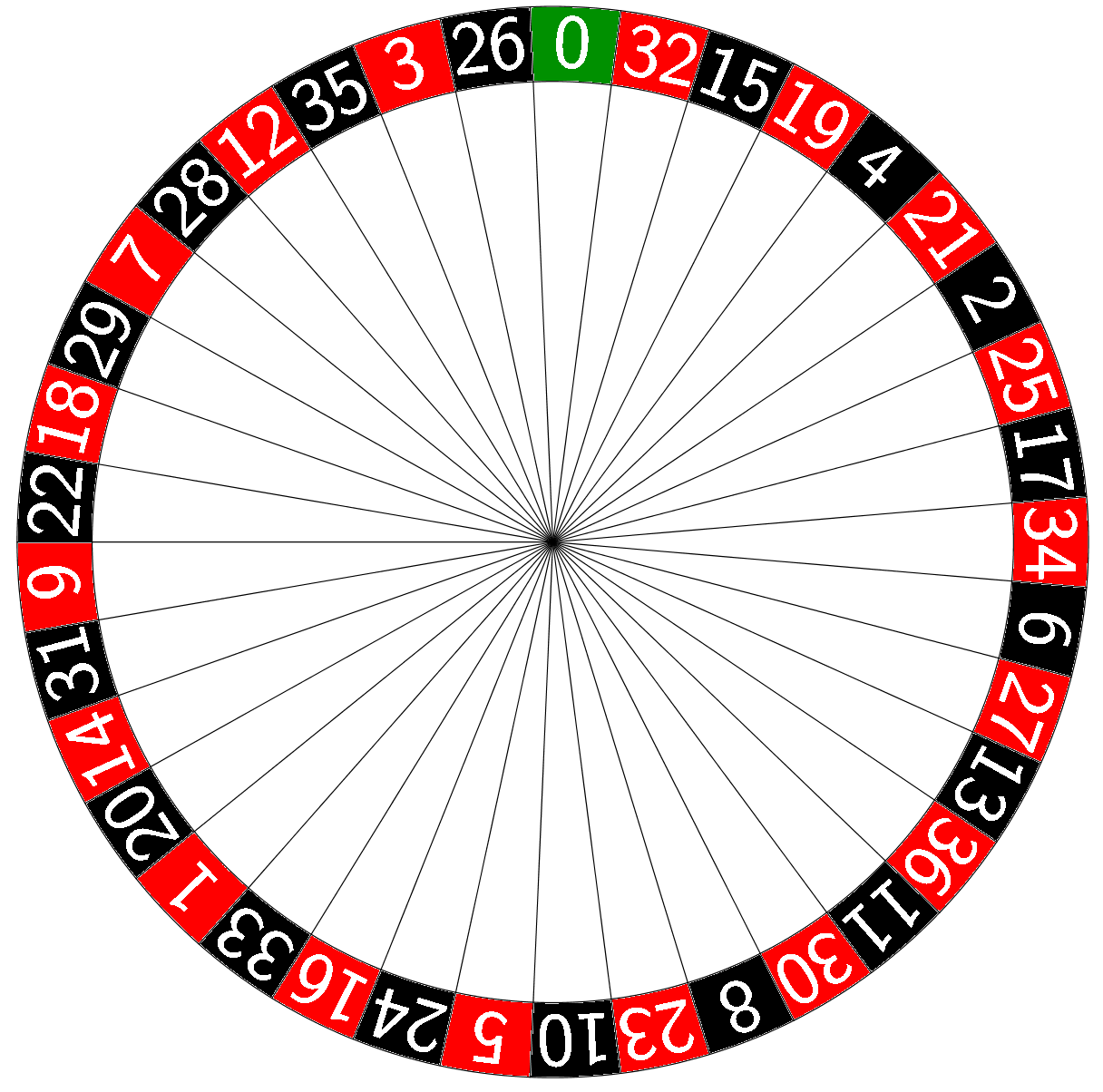
Panos (pelimerkki tms.) asetetaan pelipöydälle haluttuun ruutuun tai ruutujen reunoille, ja voiton osuessa kohdalle panos saadaan takaisin seuraavan taulukon mukaisesti.
| Kohde | Kerroin | Selite |
|---|---|---|
| Yksi numero | 36 | Pelimerkki yhdellä numerolla |
| Kaksi numeroa | 18 | Pelimerkki kahden numeron rajalla |
| Kolme numeroa | 12 | Pelimerkki rivin päässä |
| Neljä numeroa | 9 | Pelimerkki neljän numeron rajalla |
| Kuusi numeroa | 6 | Pelimerkki kahden rivin päässä rajalla |
| Tusinat | 3 | 1-12, 13-24 tai 25-36 |
| Sarakkeet | 3 | Pelimerkki sarakkeen päässä olevassa tyhjässä ruudussa |
| Väri | 2 | Punainen tai musta |
| Pieni / Suuri | 2 | 1-18 tai 19-36 |
| Parillinen / Pariton | 2 | Even (parillinen) tai Odd (pariton) |
Esimerkki: Millä todennäköisyydellä ruletista tulee
a) punainen
\(\mathsf{P(\text{punainen}) = \dfrac{18}{37} = \text{0,486...} \approx 49\:\%}\)
b) oikeanpuoleisin sarake
\(\mathsf{P(\text{sarake}) = \dfrac{12}{37} = \text{0,324...} \approx 32\:\%}\)
c) 4, 5, 7 tai 8?
\(\mathsf{P(\text{4,5,7 tai 8}) = \dfrac{4}{37} = \text{0,108...} \approx 11\:\%}\)
Esimerkki: Tiina panostaa yhden pelimerkin punaiselle ja toisen parittomalle (ODD).
a) Millä todennäköisyydellä molemmat osuvat?
b) Mikä on Tiinan panostuksen palautusprosentti?
Ratkaisut:
a) \(\mathsf{P(\text{pariton punainen}) = \dfrac{10}{37} = \text{0,270...} \approx 27\:\%}\)
b) Listataan kaikki mahdolliset tapahtumat, kertoimet, voitot / tappiot panoksen vähentämisen jälkeen (panos on nyt 2) sekä tapahtuman todennäköisyys.
| Tapahtuma | Kerroin | Voitto | Todennäköisyys |
|---|---|---|---|
| Punainen (ei pariton) 12, 14, 16, 18, 30, 32, 34, 36 |
2 | 0 | \(\mathsf{\dfrac{8}{37} \approx 22\:\%}\) |
| Pariton (ei punainen) 11, 13, 15, 17, 29, 31, 33, 35 |
2 | 0 | \(\mathsf{\dfrac{8}{37} \approx 22\:\%}\) |
| Pariton punainen 1, 3, 5, 7, 9, 19, 21, 23, 25, 27 |
4 | 2 | \(\mathsf{\dfrac{10}{37} \approx 27\:\%}\) |
| Ei kumpikaan 0, 2, 4, 6, 8, 10, 20, 22, 24, 26, 28 |
0 | -2 | \(\mathsf{\dfrac{11}{37} \approx 30\:\%}\) |
Palautusprosentti:
\(\mathsf{0 \cdot \dfrac{8}{37} + 0 \cdot \dfrac{8}{37} + 2 \cdot \dfrac{10}{37} - 2 \cdot \dfrac{11}{37} = \dfrac{20}{37} - \dfrac{22}{37} = -\dfrac{2}{37}}\)
\(\mathsf{100\:\% - \dfrac{2}{37} = 100\:\% - \text{5,405...}\:\% = \text{94,59...}\:\% \approx \text{94,6}\:\%}\)
\(\begin{align}&\mathsf{0 \cdot \dfrac{8}{37} + 0 \cdot \dfrac{8}{37} + 2 \cdot \dfrac{10}{37} - 2 \cdot \dfrac{11}{37}}\\ &= \mathsf{\dfrac{20}{37} - \dfrac{22}{37}}\\ &= \mathsf{-\dfrac{2}{37}}\end{align}\)
\(\begin{align}&\mathsf{100\:\% - \dfrac{2}{37}}\\ &= \mathsf{100\:\% - \text{5,405...}\:\%}\\ &= \textsf{94,59... %}\\ &\approx \textsf{94,6 %}\end{align}\)
Vastaus: Tiinan panostuksen palautusprosentti on 94,6 prosenttia.
Hedelmäpeli
Hedelmäpeli on rahapeliautomaatti, joka koostuu useammasta rullasta, joissa on erilaisia kuvioita (alunperin hedelmiä, siitä nimitys hedelmäpeli). Rullia pyöritetään ja rullista näkyvät kuviot arvotaan satunnaisesti. Pelin tavoitteena on saada jokin ennalta määritelty kuvioyhdistelmä, josta voittaa jonkin kertoimen mukaisesti panoksensa takaisin. Kuvioiden asettelemisella rulliin, voidaan vaikuttaa kuvioyhdistelmien todennäköisyyksiin ja määrittää (peliyhtiön kannalta) sopivat kertoimet.
Käytetään esimerkeissä (ja useimmissa tehtävissä) hedelmäpeliä, jossa on kolme rullaa. Rullissa on seuraavanlaiset kuviot.
| 1 | 2 | 3 |
|---|---|---|
| 🍀 | 🍀 | 🍀 |
| 🍒 | 🍒 | 🍇 |
| 🍊 | 🍊 | 🔔 |
| 🍋 | 🍒 | 🍋 |
| 🍇 | 🍇 | 🍊 |
| 🍒 | 🍒 | 🍇 |
| 🍊 | 🍊 | 🍋 |
| 🍋 | 🍒 | 🍇 |
| 🔔 | 🔔 | 🍋 |
| 🍋 | 🍒 | 🍊 |
Esimerkki: Millä todennäköisyydellä
a) ensimmäisestä rullasta saadaan sitruuna
\(\mathsf{P(\text{1. sitruuna}) = \dfrac{3}{10} = \text{0,3} = 30\:\%}\)
b) kahdesta ensimmäisestä rullasta saadaan appelsiinit
\(\mathsf{P(\text{1. ja 2. appelsiini}) = \dfrac{2}{10} \cdot \dfrac{2}{10} = \dfrac{4}{100} = \text{0,04} = 4\:\%}\)
\(\begin{align}&\mathsf{P(\text{1. ja 2. appelsiini})}\\ &= \mathsf{\dfrac{2}{10} \cdot \dfrac{2}{10}}\\ &= \mathsf{\dfrac{4}{100}}\\ &= \textsf{0,04}\\ &= \textsf{4 %}\end{align}\)
c) saadaan kuvioyhdistelmä 🍒🍒🍊?
\(\mathsf{P(\text{2 kirsikkaa ja appelsiini}) = \dfrac{2}{10} \cdot \dfrac{5}{10} \cdot \dfrac{2}{10} = \dfrac{20}{1000} = \text{0,02} = \text{2}\:\%}\)
\(\begin{align}&\mathsf{P(\text{2 kirsikkaa ja appelsiini})}\\ &= \mathsf{\dfrac{2}{10} \cdot \dfrac{5}{10} \cdot \dfrac{2}{10}}\\ &= \mathsf{\dfrac{20}{1000}}\\ &= \textsf{0,02}\\ &= \textsf{2 %}\end{align}\)