MA9 Jakso 4: Yhtälöparit ja epäyhtälöt
1. Kertausta
Polynomit
Termi koostuu kertoimesta sekä muuttujaosasta. Muuttujaosan eksponentti kertoo termin asteen. 0. asteen termiä kutsutaan vakiotermiksi. Samanmuotoisia termejä voidaan laskea yhteen ja vähentää toisistaan eli sieventää.
\(\mathsf{4x^2 + 2x - 5 - 5x + 6 = 4x^2 - 3x + 1}\)
Polynomi koostuu yhdestä tai useammasta termistä. Polynomien summa ja erotus merkittäessä jälkimmäinen polynomi on merkittävä sulkeisiin ja laskutoimitusmerkki vaikuttaa siis koko polynomiin.
Esimerkki: Sievennä.
a)
\(\begin{align}&\mathsf{2x + 1 + (-x + 6)}\\ =\;&\mathsf{2x + 1 - x + 6}\\ =\;&\mathsf{x + 7}\end{align}\)
b)
\(\begin{align}&\mathsf{-x + 5 - (5x - 12)}\\ =\;&\mathsf{-x + 5 - 5x + 12}\\ =\;&\mathsf{-6x +17}\end{align}\)
Huomaa, että vähennyslaskussa miinusmerkki vaihtaa kaikkien polynomin termien etumerkin.
Polynomien tulossa kerrottavien polynomien termit kerrotaan keskenään.
Esimerkki: Laske.
Polynomin jakaminen vakiolla kohdistaa jakolaskun erikseen kaikkiin polynomin termeihin.
Esimerkki: Sievennä.
\(\begin{align}&\mathsf{\dfrac{-4x^2 + 8x + 14}{-2}}\\ =\;&\mathsf{\dfrac{-4x^2}{-2} + \dfrac{8x}{-2} + \dfrac{14}{-2}}\\ =\;&\mathsf{2x^2 - 4x - 7}\end{align}\)
Yhtälönratkaisu
Ensimmäisen asteen yhtälö
Ensimmäisen asteen yhtälöitä ratkaistiin vaiheittain lisäämällä, vähentämällä, kertomalla tai jakamalla yhtälöä puolittain tavoitteena saada muuttuja (yleensä x) jäämään yksin yhtälön toiselle puolelle. Puolittain suoritettavaa laskutoimitusta merkittiin yhtälön rivin perään \(||\)-merkkien jälkeen.
Esimerkki: Ratkaise yhtälö.
a)
\(\begin{align}\mathsf{2x+1} &= \mathsf{7} &&\mathsf{|| -1}\\\mathsf{2x} &= \mathsf{6} &&\mathsf{|| :2}\\\mathsf{x} &= \mathsf{3}\end{align}\)
b)
\(\begin{align}\mathsf{-3x+2} &= \mathsf{x + 10} &&\mathsf{|| -x}\\\mathsf{-4x+2} &= \mathsf{10} &&\mathsf{|| -2}\\\mathsf{-4x} &= \mathsf{8} &&\mathsf{|| :(-4)}\\\mathsf{x} &= \mathsf{-2}\end{align}\)
Yhtälönratkaisun avulla voidaan myös muokata useamman muuttujan yhtälöitä. Suoran yhtälö voidaan esittää ratkaistussa muodossa (esim. \(\mathsf{y = -2x + 3}\) tai yleisessä muodossa (\(\mathsf{2x + y - 3 = 0}\)). Suoran yhtälöä tulee osata muokata näiden muotojen välillä suoran piirtämisen tai muun ratkaisemisen vuoksi.
Esimerkki: Ratkaise yhtälö muuttujan y suhteen.
\(\begin{align}\mathsf{-6x+2y-8} &= \mathsf{0} &&\mathsf{|| +6x}\\\mathsf{2y-8} &= \mathsf{}6x &&\mathsf{|| +8}\\\mathsf{2y} &= \mathsf{6x + 8} &&\mathsf{|| :2}\\\mathsf{y} &= \mathsf{3x + 4}\end{align}\)
Suora
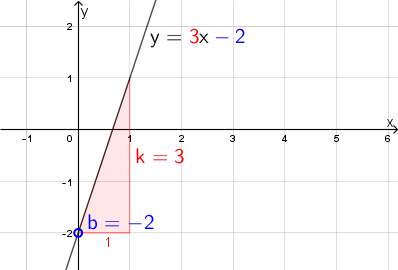
Suoran yhtälö on muotoa \(\mathsf{y = kx + b}\), jonka avulla voidaan laskea suoran pisteitä sijoittamalla x-koordinaatin arvoja suoran yhtälöön ja ratkaisemalla niitä vastaavat y-koordinaatit.
Suoran yhtälössä kerrointa \(\mathsf{k}\) kutsuttiin kulmakertoimeksi (kaltevuus) ja kerrointa \(\mathsf{b}\) vakiotermiksi (y-akselin leikkauskohta). Näiden avulla voitiin piirtää suoran kuvaaja ilman erillistä koordinaattien laskemista.
- Vakiotermi kertoo suoran ja y-akselin leikkauskohdan.
- Kulmakerroin kertoo y-akselin suuntaisen muutoksen, kun siirrytään edellisestä suoran pisteestä x-akselin suunnassa yhden verran oikealle.
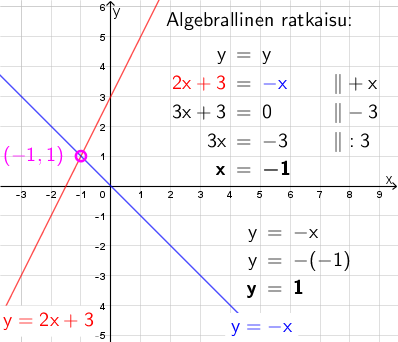
Suorien leikkauspiste voidaan ratkaista joko graafisesti tai algebrallisesti. Graafisessa ratkaisussa suorat piirretään samaan koordinaatistoon, ja leikkaupiste määritetään silmämääräisesti kuvasta. Algebrallisessa ratkaisussa suorien lausekkeet merkitään yhtä suuriksi, ratkaistaan muodostuneesta yhtälöstä x-koordinaatin arvo ja lopuksi selvitetään y-koordinaatin arvo sijoittamalla saatu x-koordinaatti toiseen suoran yhtälöön.
2. Yhtälöpari
Yhtälönratkaisun tarkoituksena on ratkaista tuntemattoman muuttujan arvo. Toistaiseksi muuttujia yhtälöissä on ollut vain yksi, jolloin ollaan selvitty yhden yhtälön ratkaisemisella. Jos yhtälössä on kaksi muuttujaa, tarvitaan yhtälöitäkin kaksi molempien muuttujien ratkaisemiseksi. Tällöin kyseessä on yhtälöpari.
Yhtälöpari merkitään kirjoittamalla yhtälöt allekkain, ja piirtämällä yhtälöiden vasemmalle puolelle aaltosulje.
\(\begin{cases}\mathsf{2x+y = 4}\\ \mathsf{-x-y = -1}\end{cases}\)
Ratkaisun tutkiminen
Koska muuttujia yhtälöissä on kaksi, niin ratkaisukin on lukupari \(\mathsf{(x,y)}\). Yhtälöparin ratkaisemista harjoitellaan myöhemmissä luvuissa. Yhtälöparin ratkaisua voidaan tutkia sijoittamalla muuttujien arvot yhtälöihin, ja testaamalla toteuttaako lukupari molemmat yhtälöt.
Esimerkki: Toteuttaako lukupari \(\mathsf{(x,y) = (-2, 8)}\) yhtälöparin \(\begin{cases}\mathsf{2x+y = 4}\\ \mathsf{-x-y = -1}\end{cases}\) ?
Ylempi yhtälö:
\(\begin{align}\mathsf{2x+y} &= \mathsf{4}\\ \mathsf{2 \cdot (-2) + 8} &= \mathsf{4}\\ \mathsf{-4+8} &= \mathsf{4}\\ \mathsf{4} &= \mathsf{4}\end{align}\)
Yhtälö on tosi.
Alempi yhtälö:
\(\begin{align}\mathsf{-x-y} &= \mathsf{-1}\\ \mathsf{-(-2) - 8} &= \mathsf{-1}\\ \mathsf{2-8} &= \mathsf{-1}\\ \mathsf{-6} &= \mathsf{-1}\end{align}\)
Yhtälö on epätosi.
Vastaus: Lukupari ei ole yhtälöparin ratkaisu.
Jos lukupari toteuttaa molemmat yhtälöt, lukupari on myös yhtälöparin ratkaisu. Jos jompi kumpi yhtälöistä ei toteudu, ei lukupari toteuta myöskään yhtälöparia.
3. Graafinen ratkaisu
Yhtälöpari voidaan ratkaista graafisesti piirtämällä yhtälöitä vastaavat suorat koordinaatistoon. Suorien leikkuspiste on yhtälöparin ratkaisu.
Esimerkki Ratkaise yhtälöpari graafisesti.
\(\begin{cases}\mathsf{y = 2x - 3}\\ \mathsf{y = -x+3}\end{cases}\)
Piirretään suorat.
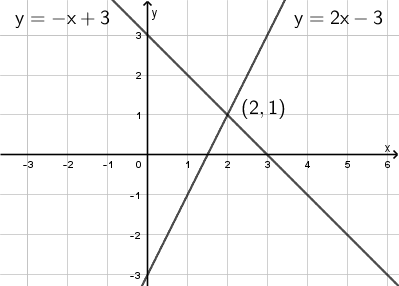
Vastaus: \(\mathsf{(x,y) = (2,1)}\)
Jos yhtälöt eivät ole ratkaistussa muodossa, ne täytyy ennen piirtämistä ratkaista muuttujan y suhteen.
Esimerkki Ratkaise yhtälöpari graafisesti.
\(\begin{cases}\mathsf{-x + 2y + 2 = 0}\\ \mathsf{y = 2x+5}\end{cases}\)
Ratkaistaan ylempi yhtälö muuttujan y suhteen.
\(\begin{align}\mathsf{-x+2y+2} &= \mathsf{0} &&\mathsf{\|+x}\\ \mathsf{2y+2} &= \mathsf{x} &&\mathsf{\|-2}\\ \mathsf{2y} &= \mathsf{x-2} &&\mathsf{\|:2}\\ \mathsf{y} &= \mathsf{\dfrac{1}{2}x-1}\end{align}\)
Piirretään suorat.
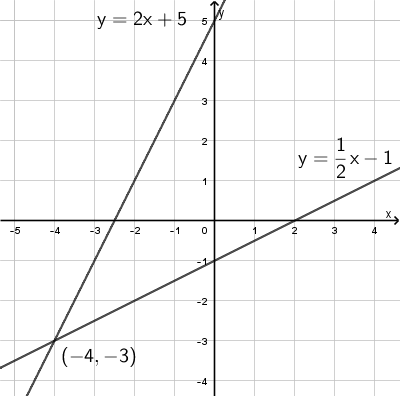
Vastaus: \(\mathsf{(x,y) = (-4,-3)}\)
4. Sijoitusmenetelmä
Sijoitusmenetelmä on algebrallinen tapa ratkaista yhtälöpari. Sijoitusmenetemää on järkevää käyttää silloin, kun vähintään toinen yhtälöistä on ratkaistu joko muuttujan x tai y suhteen. Sijoitusmenetelmää voidaan käyttää kahdella eri tavalla hieman tilanteesta riippuen.
Molemmat yhtälöt ratkaistussa muodossa
Jos molemmat yhtälöt ovat ratkaistussa muodossa saman muuttujan (yleensä y) suhteen, voidaan lausekkeista muodostaa yhtälö ja ratkaista sen avulla toisen muuttujan arvo (yleensä x). Tämän jälkeen pitää vielä ratkaista toisen muuttujan arvo sijoittamalla saatu arvo jompaan kumpaan yhtälöön.
Esimerkki: Ratkaise yhtälöpari sijoitusmenetelmän avulla.
\(\begin{cases}\mathsf{y=2x-8}\\ \mathsf{y=x-6}\end{cases}\)
Koska \(\mathsf{y=y}\), merkitään lausekkeet yhtä suuriksi ja ratkaistaan muuttujan x arvo.
\(\begin{align}\mathsf{2x-8} &= \mathsf{x-6} &&\mathsf{\|-x}\\ \mathsf{x-8} &= \mathsf{-6} &&\mathsf{\|+8}\\ \mathsf{x} &= \mathsf{2}\end{align}\)
Ratkaistaan muuttujan y arvo sijoittamalla saatu \(\mathsf{x=2}\) toiseen alkuperäisistä yhtälöistä.
\(\begin{align}\mathsf{y} &= \mathsf{x-6}\\ &= \mathsf{2-6}\\ &= \mathsf{-4}\end{align}\)
Vastaus: \(\mathsf{(x,y) = (2,-4)}\)
Vain toinen yhtälö on ratkaistussa muodossa
Aina yhtälöparin molemmat yhtälöt eivät ole kauniisti ratkaistussa muodossa. Vaihtoehtoja on kaksi: ratkaistaan molemmat yhtälöt saman muuttujan suhteen ja toimitaan kuten edellisessä esimerkissä, tai sijoitetaan ratkaistussa muodossa olevan yhtälön lauseke toiseen yhtälöön kyseisen muuttujan paikalle. Tarkastellaan seuraavassa esimerkissä jälkimmäistä tapaa.
Esimerkki: Ratkaise yhtälöpari sijoitusmenetelmän avulla.
\(\begin{cases}\mathsf{y=2x-3}\\ \mathsf{2x+2y=6}\end{cases}\)
Ratkaistaan muuttujan x arvo sijoittamalla lauseke \(\mathsf{2x-3}\) alempaan yhtälöön muuttujan y paikalle ja ratkaisemalla yhtälö.
\(\begin{align}\mathsf{2x+2y} &= \mathsf{6} &&\mathsf{\|\;y=2x-3}\\ \mathsf{2x+2\cdot(2x-3)} &= \mathsf{6}\\ \mathsf{2x+4x-6} &= \mathsf{6}\\ \mathsf{6x-6} &= \mathsf{6} &&\mathsf{\|+6}\\ \mathsf{6x} &= \mathsf{12} &&\mathsf{\|:6}\\ \mathsf{x} &= \mathsf{2}\end{align}\)
Ratkaistaan muuttujan y arvo sijoittamalla saatu \(\mathsf{x=2}\) toiseen alkuperäisistä yhtälöistä.
\(\begin{align}\mathsf{y} &= \mathsf{2x-3}\\ &= \mathsf{2 \cdot 2 - 3}\\ &= \mathsf{4-3}\\ &=\mathsf{1}\end{align}\)
Vastaus: \(\mathsf{(x,y) = (2, 1)}\)
5. Yhteenlaskumenetelmä
Toinen algebrallinen tapa yhtälöparin ratkaisemiseen on yhteenlaskumenetelmä. Yhteenlaskumenetelmää on järkevää käyttää silloin, kun molemmat muuttujista x ja y ovat samalla puolella yhtälöä. Lisäksi toisen muuttujista tulisi sieventyä yhteenlaskun jälkeen pois, jotta jäljelle jää yhden muuttujan yhtälö.
Esimerkki: Ratkaise yhtälöpari yhteenlaskumenetelmän avulla.
Esimerkissä muuttuja y sieveni pois kun yhtälöiden y-termit olivat toistensa vastatermejä (kertoimet vastalukuja). Näin ei suinkaan aina ole, vaan yhtälöitä on joskus muokattava ennen yhteenlaskua, jotta yhteenlaskussa toinen muuttuja sievenee pois.
Esimerkki: Ratkaise yhtälöpari yhteenlaskumenetelmän avulla.
6. Sanallisia tehtäviä
Matematiikassa sanalliseen muotoon kirjoitettujen "käytännön ongelmien" ratkaisemiseen voidaan käyttää monia eri tapoja ja työkaluja. Koulumatematiikan tarkoitus on tarjota oppilaan työkalupakkiin monia tällaisia työkaluja, joista yhtälöparit ovat yksi konkreettinen esimerkki. Kaikkiin tilanteisiin ne eivät sovi, mutta tutkittaessa kahta kohdetta ja niiden ominaisuuksia, voidaan tunnetuista tiedoista saada yhtälöparien avulla ratkaistua tuntemattomia asioita.
Kaksi kohdetta, yksi ominaisuus
Yksi yleinen yhtälöparien avulla ratkaistava tilanne tarkastelee kahta kohdetta (esim. ihmistä) joilla on jokin ominaisuus (ikä, työtunnit, raha,...). Näiden ominaisuuksien tarkkaa määrää ei tunneta, mutta niiden välisestä suhteesta tiedetään jotain.
Esimerkki: Jyrillä ja Jannella on yhteensä 68 lakupötköä. Jyrillä on 20 lakupötköä enemmän kuin Jannella. Kuinka monta lakupötköä Jyrillä ja Jannella on?
Kohteet ja ominaisuudet:
Jyri: \(\mathsf{x}\) lakupötköä
Janne: \(\mathsf{y}\) lakupötköä
Ominaisuuksien väliset suhteet:
"Jyrillä ja Jannella on yhteensä 68 lakupötköä." eli
\(\mathsf{x+y=68}\)
"Jyrillä on 20 lakupötköä enemmän kuin Jannella." eli
\(\mathsf{x-y=20}\) tai \(\mathsf{x = y + 20}\)
Muodostetaan yhtälöpari:
\(\begin{cases}\mathsf{x+y}=\mathsf{68}\\ \mathsf{x-y} = \mathsf{20}\end{cases}\)
Ratkaistaan yhtälöpari esimerkiksi yhteenlaskumenetelmällä:
\(\underline{+\begin{cases}\mathsf{x+y = 68}\\ \mathsf{x-y = 20}\end{cases}}\)
\(\begin{aligned} \rule{2.9em}{0pt}\mathsf{2x}&= \mathsf{88} &&\mathsf{\|:2}\\ \mathsf{x} &= \mathsf{44} \end{aligned}\)
\(\begin{aligned} \mathsf{x+y} &= \mathsf{68}\\ \mathsf{44+y}&= \mathsf{68} &&\mathsf{\|-44}\\ \mathsf{y} &= \mathsf{24}\end{aligned}\)
Vastaus: Jyrillä on 44 lakupötköä ja Jannella on 24 lakupötköä.
Kaksi kohdetta, kaksi ominaisuutta
Toinen yleinen yhtälöparien avulla ratkaistava tilanne tarkastelee myös kahta kohdetta (esim. ihmistä, eläintä, elokuvalippua) joilla on jotkin kaksi ominaisuutta (lukumäärä, hinta, aika, massa,...), joiden avulla voidaan muodostaa kaksi yhtälöä.
Esimerkki: Kaupasta ostettiin maitoa (1 € / litra) ja jugurttia (3 € / litra) yhteensä 14 litraa ja ostokset maksoivat 24 euroa. Kuinka monta litran purkkia maitoa ja jugurttia ostettiin?
Kohteet ja ominaisuudet:
Maito: Lukumäärä: \(\mathsf{x}\) kappaletta, hinta: \(\mathsf{1 \cdot x = x}\) euroa.
Jugurtti: Lukumäärä: \(\mathsf{y}\) kappaletta, hinta: \(\mathsf{3 \cdot y = 3y}\) euroa.
Ominaisuuksien väliset suhteet:
"yhteensä 14 litraa" eli
\(\mathsf{x+y=14}\)
"ostokset maksoivat 24 euroa" eli
\(\mathsf{x+3y=24}\)
Muodostetaan yhtälöpari:
\(\left\{\begin{aligned} \mathsf{x+y}&=\mathsf{14}\\ \mathsf{x+3y}&= \mathsf{24}\end{aligned}\right.\)
Ratkaistaan yhtälöpari esimerkiksi yhteenlaskumenetelmällä:
\(\begin{cases} \mathsf{x+y = 14\qquad\|\cdot(-1)}\\ \mathsf{x+3y = 24}\end{cases}\)
\(\underline{+\left\{\begin{aligned} \mathsf{-x-y} &= \mathsf{-14}\\ \mathsf{x+3y} &= \mathsf{24}\end{aligned}\right.}\)
\(\begin{aligned} \rule{3.7em}{0pt}\mathsf{2y}&= \mathsf{10} &&\mathsf{\|:2}\\ \mathsf{y} &= \mathsf{5} \end{aligned}\)
\(\begin{aligned} \mathsf{x+y} &= \mathsf{14}\\ \mathsf{x+5}&= \mathsf{14} &&\|\mathsf{-5}\\ \mathsf{x} &= \mathsf{9}\end{aligned}\)
Vastaus: Maitojapurkkeja ostettiin 9 kappaletta ja jugurttipurkkeja 5 kappaletta.
7. Epäyhtälöt
Epäyhtälö on kuten yhtälö, mutta yhtäsuuruusmerkin sijaan lausekkeiden välissä on jokin suuruusvertailumerkki. Epäyhtälöllä on usein useita, jopa ääretön määrä, ratkaisuja. Niiden avulla voidaan siis rajata ja valita sopivia lukujoukkoja.
Suuruusvertailumerkit
Yhtäsuuruuteen liittyvät vertailumerkit =, ≠ ja ≈ lienevät jo tuttuja, mutta epäyhtälöissä käytettäviä vertailumerkkejä <, >, ≤ ja ≥ on käytetty vain lyhyesti kahden luvun suuruutta vertailtaessa. Jos toisena vertailun kohteena on muuttuja x, ne rajaavat muuttujan arvoja yhdestä suunnasta, jolloin ratkaisuja on ääretön määrä. Ratkaisu voidaan ilmoittaa numeerisesti luettelemalla osa ratkaisujoukon luvuista tai graafisesti piirtämällä lukujoukkoa vastaava puolisuora lukusuoralle. Jos käytetään yhtäsuuruuden hyväksyviä vertailumerkkejä ≤ ja ≥ vertailuarvo merkitään täytetyllä ympyrällä. Vastaavasti < ja > merkkien tapauksessa merkki jätetään ontoksi, jolloin korostetaan sitä, että kyseinen vertailuarvo ei kuulu ratkaisujoukkoon.
| Merkki | Selitys |
|---|---|
| = | Yhtä suuri kuin |
| < | Pienempi kuin |
| > | Suurempi kuin |
| ≤ | Pienempi tai yhtä suuri kuin |
| ≥ | Suurempi tai yhtä suuri kuin |
| ≠ | Yhtä suuri kuin |
| ≈ | Yhtä suuri kuin |
Esimerkki: Mikä kokonaisluku sopii muuttujan x paikalle?
a) \(\mathsf{x=4}\)
Numeerinen ratkaisu:
\(\mathsf{4}\)
Graafinen ratkaisu:

b) \(\mathsf{x<4}\)
Numeerinen ratkaisu:
\(\mathsf{..., 1, 2, 3}\)
Graafinen ratkaisu:

c) \(\mathsf{x>4}\)
Numeerinen ratkaisu:
\(\mathsf{5,6,7,...}\)
Graafinen ratkaisu:

d) \(\mathsf{x \leq 4}\)
Numeerinen ratkaisu:
\(\mathsf{..., 2, 3, 4}\)
Graafinen ratkaisu:

e) \(\mathsf{x \geq 4}\)
Numeerinen ratkaisu:
\(\mathsf{4,5,6,...}\)
Graafinen ratkaisu:

f) \(\mathsf{x \neq 4}\)
Numeerinen ratkaisu:
\(\mathsf{...2, 3, 5, 6, ...}\)
Graafinen ratkaisu:

Välin merkitseminen
Jos muuttujan x arvo halutaan rajata jollekkin välille ja saada (ainakin kokonaislukujen tapauksessa) äärellinen ratkaisu, voidaan käyttää lukuvälimerkintää.
\(\mathsf{\text{alaraja} < x < \text{yläraja}}\)
Lisäksi yhtäsuuruuden hyväksyvillä merkeillä ≤ ja ≥ voidaan määrittää lukuväli avoimeksi tai suljetuksi. Avoimessa välissä välin päätepisteet eivät kuulu mukaan lukujoukkoon. Suljetussa välissä päätepisteet kuuluvat mukaan lukujoukkoon. Alla olevassa esimerkissä on esitetty erilaiset lukuvälit kokonaislukujen tapauksessa.
Esimerkki: Mikä kokonaisluku sopii muuttujan x paikalle?
a) avoin väli \(\mathsf{3 < x < 5}\)
Numeerinen ratkaisu:
\(\mathsf{4}\)
Graafinen ratkaisu:

b) suljettu väli \(\mathsf{3 \leq x \leq 5}\)
Numeerinen ratkaisu:
\(\mathsf{3, 4, 5}\)
Graafinen ratkaisu:

c) vasemmalta avoin väli \(\mathsf{3 < x \leq 5}\)
Numeerinen ratkaisu:
\(\mathsf{4, 5}\)
Graafinen ratkaisu:

d) oikealta avoin väli \(\mathsf{3 \leq x < 5}\)
Numeerinen ratkaisu:
\(\mathsf{3, 4}\)
Graafinen ratkaisu:

Ratkaisun tutkiminen
Ennen varsinaisia epäyhtälön ratkatkaisumenetelmiä tutustutaan epäyhtälön ratkaisun tutkimiseen annetulla muuttujan arvolla. Menetelmä on tuttu yhtälöiden parista, eli sijoitetaan muuttujan arvo epäyhtälöön, lasketaan lausekkeiden arvot ja tehdään johtopäätös yksinkertaisen epäyhtälön perusteella.
Esimerkki: Tutki, onko \(\mathsf{x=1}\) epäyhtälön \(\mathsf{-x+4>0}\) ratkaisu.
\(\begin{align}\mathsf{-x+4} &> \mathsf{0}\\ \mathsf{-1+4} &> \mathsf{0}\\ \mathsf{3} &> \mathsf{0}\end{align}\)
Epäyhtälö on tosi.
Vastaus: \(\mathsf{x=1}\) on epäyhtälön ratkaisu.
Esimerkki: Tutki, onko \(\mathsf{x=-2}\) epäyhtälön \(\mathsf{-3x-2 \leq 2x+3}\) ratkaisu.
\(\begin{align}\mathsf{-3x-2} &\leq \mathsf{2x+3}\\ \mathsf{-3 \cdot (-2) - 2} &\leq \mathsf{2 \cdot (-2) + 3}\\ \mathsf{4} &\leq \mathsf{-1}\end{align}\)
Epäyhtälö on epätosi.
Vastaus: \(\mathsf{x=-2}\) ei ole epäyhtälön ratkaisu.
Algebrallinen ratkaisu
Epäyhtälö voidaan ratkaista lähes samalla tavalla kuin tavallinenkin yhtälö. Ainoa poikkeus on negatiivisilla luvuilla kertominen ja jakaminen, jolloin epäyhtälön vertailumerkki on käännettävä toiseen suuntaan.
Esimerkki: Ratkaise epäyhtälö \(\mathsf{-2x+3 > 1}\) algebrallisesti.
\(\begin{align}\mathsf{-2x+3} &> \mathsf{1} &&\mathsf{\|-3}\\ \mathsf{-2x} &> \mathsf{-2} &&\mathsf{\|:(-2)}\\ \mathsf{x} &< \mathsf{1}\end{align}\)
Vastaus: Epäyhtälön ratkaisuja ovat kaikki muuttujan x arvot, jotka toteuttavat epäyhtälön x < 1.
Graafinen ratkaisu
Graafisessa ratkaisussa piirretään epäyhtälön molempien puolien lausekkeita vastaavat kuvaajat koordinaatistoon ja etsitään niiden leikkauspiste. Leikkaupisteen x-koordinaatin ympäristöä tutkimalla voidaan päätellä epäyhtälön ratkaisu.
Esimerkki: Ratkaise epäyhtälö \(\mathsf{-2x+3 > 1}\) graafisesti.
Piirretään koordinaatistoon suorat \(\mathsf{y=-2x+3}\) ja \(\mathsf{y=1}\).
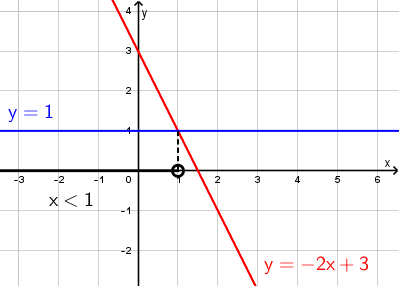
Siirryttäessä leikkauspisteestä vasemmalle epäyhtälö \(\mathsf{-2x+3 > 1}\) toteutuu, eli \(\mathsf{y = -2x+3}\) saa suurempia y:n arvoja (on ylempänä) kuin \(\mathsf{y=1}\).
Vastaus: Epäyhtälön ratkaisu on x < 1.