MA9 Jakso 1: Funktio
1. Kertausta
Funktioiden opiskelussa tarvitaan 7. luokalta lukujonojen ja koordinaatiston sekä 8. luokalta polynomien, potenssien ja yhtälöratkaisun tuntemusta. Nämä ainekset yhdistämällä saadaan tapa esittää lukujen välistä yhteyttä niin matemaattisin merkinnöin kuin koordinaatistossakin.
Potenssi ja neliöjuuri
Potenssimerkinnän avulla voidaan lyhentää kertolaskua, missä sama luku esiintyy tulon tekijänä useamman kerran. Potenssimerkinnässä tulon tekijän oikeaan yläkulmaan kirjoitetaan luku, joka kertoo kuinka monta kertaa tekijä kertolaskussa esiintyy. Esimerkiksi
\(\mathsf{2 \cdot 2 \cdot 2 \cdot 2 = 2^4}\)
Tulon tekijää (2) kutsutaan kantaluvuksi, ja yläkulmassa olevaa lukua (4) kutsutaan eksponentiksi. Kyseinen merkintä sanottaisiin "Kaksi potenssiin neljä", "Kaksi neljänteen" tai "Kaksi korotettuna neljänteen potenssiin".
Potenssin arvoa laskettaessa potenssimerkintä voidaan kirjoittaa ensin kertolaskuna, ja laskea kertolasku normaalisti tämän jälkeen.
Esimerkki: Laske.
a) \(\mathsf{6^2 = 6 \cdot 6 = 36}\)
b) \(\mathsf{7^2= 7 \cdot 7 = 49}\)
c) \(\mathsf{(-5)^2 = -5 \cdot (-5) = 25}\)
d) \(\mathsf{3^4 = 3 \cdot 3 \cdot 3 \cdot 3 = 81}\)
Kuten yllä olevasta esimerkistä huomataan, niin kantaluku voi olla myös negatiivinen. Negatiivinen kantaluku tulee kirjoittaa sulkeiden sisään. Jos sulkeita ei merkitä, potenssi ei vaikuta miinusmerkkiin, vaan miinusmerkki pysyy potenssin arvon edessä.
Esimerkki: Laske.
a) \(\mathsf{(-4)^2 = -4 \cdot (-4) = 16}\)
b) \(\mathsf{-4^2 = -4 \cdot 4 = -16}\)
Juurilaskut ovat potenssien käänteisiä laskutoimituksia. Nyt keskitytään toiseen potenssiin korottamisen käänteiseen laskutoimitukseen eli neliöjuureen.
\(\mathsf{5^2 = 25 \qquad \Rightarrow \qquad \sqrt{25} = 5}\)
Neliöjuuren merkintänä käytetään erityistä juuri-merkkiä \(\sqrt{\rule{1em}{0pt}\rule{0pt}{1em}}\). Merkin alla olevaa lukua kutsutaan juurrettavaksi. Neliöjuuri vastaa siis kysymykseen "Mikä luku on kerrottu itsellään, että saadaan vastaukseksi juurrettava?".
Yleisesti luvun \(\mathsf{x}\) neliöjuuri \(\mathsf{\sqrt{x} = a}\) on siis ei-negatiivinen luku, joka itsellään kerrottuna on luku \(\mathsf{x}\).
\(\mathsf{x = a \cdot a = a^2 \quad \Leftrightarrow \quad \sqrt{x} = a \quad}\) kun \(\mathsf{a \geq 0}\)
Esimerkki: Laske.
a) \(\mathsf{\sqrt{16} = 4}\)
b) \(\mathsf{\sqrt{36} = 6}\)
c) \(\mathsf{\sqrt{100} = 10}\)
d) \(\mathsf{\sqrt{1} = 1}\)
Termit ja polynomit
Termi on kertoimen ja muuttujaosan tulo. Kerroin on luku, ja muuttujaosassa on nimensä mukaisesti muuttuja. Muuttuja voi olla korotettuna potenssiin, jolloin sen eksponenttia kutsutaan termin asteeksi.
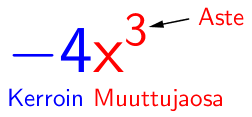
Termejä luokitellaan niiden asteen mukaan, eli esimerkiksi \(\mathsf{6x^3}\) on kolmannen asteen termi, \(\mathsf{-7x^5}\) on viidennen asteen termi jne.
Huomaathan erityisesti seuraavien termien asteet:
- Termin \(\mathsf{5x}\) aste on 1, sillä \(\mathsf{5x = 5x^1}\).
- Vakiotermin \(\mathsf{-2}\) aste on 0, sillä \(\mathsf{-2 = -2x^0}\).
Termit ovat samanmuotoisia, jos niillä on täsmälleen sama muuttujaosa, eli siis sama muuttuja sekä aste. Vain samanmuotoisia termejä voidaan laskea yhteen ja vähentää toisistaan.
Esimerkki: Sievennä.
a) \(\mathsf{2x^2 + 3x^2 = 5x^2}\)
b) \(\mathsf{4x^3 - 5x^3 = -x^3}\)
c) \(\mathsf{6x^2 + 4x^2 + 3x - x = 10x^2 + 2x}\)
d) \(\begin{align}&\mathsf{{\color{red}5x^3}\;{\color{blue}-\;2x^2} + 6 \;{\color{red}-\;x^3}\;{\color{blue}+\;3x^2} -7}\\ =\;&\mathsf{{\color{red}4x^3} \;{\color{blue}+\;x^2} - 1}\end{align}\)
Termien kerto- ja jakolaskussa kertoimet kerrotaan (jaetaan) erikseen ja muuttujaosat erikseen.
Esimerkki: Sievennä.
a) \(\mathsf{{\color{red}2}{\color{blue}x^2} \cdot {\color{red}3}{\color{blue}x^3} = {\color{red}6}{\color{blue}x^5}}\)
b) \(\mathsf{{\color{red}-}{\color{blue}x} \cdot {\color{red}4}{\color{blue}x^2} = {\color{red}-4}{\color{blue}x^3}}\)
c) \(\mathsf{\dfrac{{\color{red}12}{\color{blue}x^3}}{{\color{red}4}{\color{blue}x^2}} = {\color{red}3}{\color{blue}x}}\)
d) \(\mathsf{\dfrac{{\color{red}-42}{\color{blue}x^7}}{{\color{red}7}{\color{blue}x^3}} = {\color{red}-6}{\color{blue}x^4}}\)
Termillä voidaan kertoa myös kokonaista polynomia. Kertolasku kohdistuu kaikkiin polynomin termeihin.
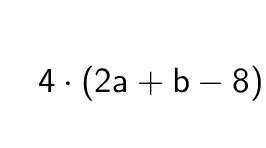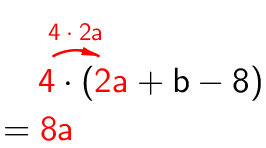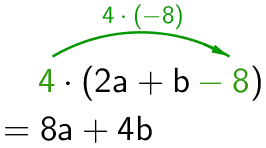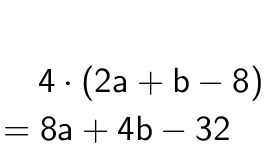
Jos muuttujan arvo tunnettaan, voidaan polynomin arvo laskea sijoittamalla arvo lausekkeeseen muuttujan paikalle.
Esimerkki: Laske lausekkeen \(\mathsf{3x + 4}\) arvo, kun muuttuja saa arvon \(\mathsf{x = 2}\).
\(\begin{align}\phantom{=}&\mathsf{3x + 4}\\ =\;&\mathsf{3\cdot 2 + 4}\\ =\;&\mathsf{6 + 4}\\ =\;&\mathsf{10}\end{align}\)
Sijoitettaessa negatiivista lukua muuttujan paikalle, tulee luku kirjoittaa sulkeiden sisään.
Esimerkki: Laske lausekkeen \(\mathsf{3x + 4}\) arvo, kun muuttuja saa arvon \(\mathsf{x = -1}\).
\(\begin{align}\phantom{=}&\mathsf{3x + 4}\\ =\;&\mathsf{3\cdot (-1) + 4}\\ =\;&\mathsf{-3 + 4}\\ =\;&\mathsf{1}\end{align}\)
Koordinaatisto ja piste
Koordinaatisto koostuu x- ja y-akselista. Paikkaa koordinaatistossa kuvataan pisteellä, jonka koordinaatit kuvaavat sijaintia koordinaatistossa x- ja y-koordinaattien avulla.
Lukujonot
Lukujono on järjestykseen asetettujen lukujen luettelo. Yksittäistä lukua kutsutaan jonon jäseneksi. Jokaisella jäsenellä on oma järjestysnumeronsa, jota merkitään usein muuttujalla \(\mathsf{n}\).
Lukujonon sääntö voidaan muodostaa kahdella eri tavalla:
- Ilmoittamalla lukujonon ensimmäinen jäsen sekä laskutoimitus, jolla seuraava jäsen lasketaan. (Sanallinen)
- muuttujalauseke, jolla voidaan laskea lukujonon järjestykseltään \(\mathsf{n}\):s jäsen. (Lauseke)
Esimerkki: Kirjoita lukujonon \(\mathsf{2, 5, 8, 11, \dots}\) sääntö sanallisesti ja lausekkeena.
Sääntö sanallisesti:
Lukujonon ensimmäinen jäsen on \(\mathsf{2}\), ja seuraava jäsen saadaan lisäämällä edelliseen luku \(\mathsf{3}\).
Sääntö lausekkeena:
Lukujonon n:s jäsen saadaan laskettua muuttujalausekkeesta \(\mathsf{3n - 1}\).
Lausekkeena annetun säännön hyöty on siinä, että lukujonon jäseniä voi laskea vapaasti, eikä edellistä jäsentä tarvitse tietää.
Esimerkki: Laske lukujonon \(\mathsf{-6n+20}\) 9. jäsen.
\(\mathsf{-6 \cdot 9 + 20 = -54 + 20 = -34}\)
Yhtälön ratkaiseminen
Yhtälön ratkaisu voidaan myös etsiä muokkaamalla yhtälöä suorittamalla laskutoimituksia yhtälön molemmille puolille. Laskutoimitukset merkitään muokattavan rivin oikealle puolelle \(\mathsf{\|}\)-merkkien jälkeen.
Esimerkki:
a) Ratkaise yhtälö \(\mathsf{3x = -12}\)
\(\begin{align}\mathsf{3x} &= \mathsf{-12} && \mathsf{\|:3}\\\mathsf{x} &= \mathsf{-4}\end{align}\)
b) Ratkaise yhtälö \(\mathsf{2x + 3 = 7}\)
\(\begin{align}\mathsf{2x + 3} &= \mathsf{7} && \mathsf{\|-3}\\\mathsf{2x} &= \mathsf{4} &&\mathsf{\|:2}\\\mathsf{x} &= \mathsf{2}\end{align}\)
c) Ratkaise yhtälö \(\mathsf{6x = -2x + 32}\)
\(\begin{align}\mathsf{6x} &= \mathsf{-2x + 32} && \mathsf{\|+2x}\\\mathsf{8x} &= \mathsf{32}&&\mathsf{\|:8}\\\mathsf{x} &= \mathsf{4}\end{align}\)
d) Ratkaise yhtälö \(\mathsf{5x + 6 = 2x - 9}\)
\(\begin{align}\mathsf{5x + 6} &= \mathsf{2x-9} && \mathsf{\|-2x}\\\mathsf{3x + 6} &= \mathsf{-9}&&\mathsf{\|-6}\\\mathsf{3x} &= \mathsf{-15}&&\mathsf{\|:3}\\\mathsf{x} &= \mathsf{-5}\end{align}\)
Toisen asteen yhtälö
Toisen asteen yhtälöllä tarkoitetaan yhtälöä, jossa esiintyy termejä, joiden aste on 2. Toisin sanoen muuttuja (esim. x) on korotettu toiseen potenssiin (neliö). Toisen asteen yhtälöitä ovat esimerkiksi:
\(\mathsf{x^2 = 36}\)
\(\mathsf{5x^2 = 20}\)
\(\mathsf{-2x^2 + 7 = -11}\)
\(\mathsf{x^2 = 4x - 3}\)
Yhtälön ratkaisemisessa käytetään aina käänteisiä laskutoimituksia puolittain, jotta muuttuja saadaan jäämään yksin toiselle puolelle yhtälöä. Toiseen potenssiin korottamiselle eli neliölle vastakkainen laskutoimitus on tietenkin neliöjuuri.
Esimerkki: Ratkaise yhtälö.
a) Ratkaise yhtälö \(\mathsf{x^2 = 36}\)
\(\begin{align}\mathsf{x^2} &= \mathsf{36} \quad &\mathsf{|| \sqrt{\quad}}\\\mathsf{x} &= \mathsf{6}\\&\textsf{tai}\\\mathsf{x} &= \mathsf{-6}\end{align}\)
b) Ratkaise yhtälö \(\mathsf{x^2 = 25}\)
\(\begin{align}\mathsf{x^2} &= \mathsf{25} \quad &\mathsf{|| \sqrt{\quad}}\\\mathsf{x} &= \mathsf{\pm5}\end{align}\)
Laskujärjestys sanoo, että potenssit ja neliöjuuret lasketaan ennen kerto- ja jakolaskuja tai yhteen- ja vähennyslaskuja. Koska yhtälönratkaisussa toimitaan aina käänteisesti myös laskujärjestyksen suhteen, suoritetaan kaikki muut ratkaisun vaiheet ennen neliöjuuren ottamista puolittain.
Esimerkki:
a) Ratkaise yhtälö \(\mathsf{5x^2 = 20}\)
\(\begin{align}\mathsf{5x^2} &= \mathsf{20} \quad &&\mathsf{|| :5}\\ \mathsf{x^2} &= \mathsf{4} &&\mathsf{|| \sqrt{\quad}}\\ \mathsf{x} &= \mathsf{\pm2} \end{align}\)
b) Ratkaise yhtälö \(\mathsf{-2x^2 + 7 = -11}\)
\(\begin{align}\mathsf{-2x^2 + 7} &= \mathsf{-11} \quad &&\mathsf{|| -7}\\ \mathsf{-2x^2} &= \mathsf{-18} \quad &&\mathsf{|| :(-2)}\\ \mathsf{x^2} &= \mathsf{9} &&\mathsf{|| \sqrt{\quad}}\\ \mathsf{x} &= \mathsf{\pm3} \end{align}\)
2. Funktio
Funktio on matemaattinen tapa merkitä sääntöä tai riippuvuutta. Funktio yhdistää muuttujan arvon ja funktion arvon toisiinsa tietyn säännön mukaan. Sääntö ilmaistaan muuttujalausekkeena. Jos funktio \(\mathsf{f}\) kuvaisi sääntöä, jossa funktion arvo saadaan kertomalla muuttujan arvo kahdella ja lisäämällä tuloon yksi, funktion sääntö merkittäisiin
\(\mathsf{f(x)=2x+1}\)
Kirjain \(\mathsf{f}\) on siis funktion nimi, suluissa oleva \(\mathsf{x}\) on muuttuja ja \(\mathsf{2x+1}\) on funktion lauseke.
Funktion arvo
Sijoittamalla funktion lausekkeeseen jokin muuttujan arvo, saadaan laskettua funktion arvo. Tällöin myös funktion merkinnässä muuttuja korvataan muuttujan arvolla.
Esimerkki: Merkitse ja laske funktion \(\mathsf{f(x)=2x+1}\) arvo, kun
a) \(\mathsf{x = 2}\)
\(\begin{align}\mathsf{f(2)} &= \mathsf{2 \cdot 2 + 1}\\ &= \mathsf{4+1}\\ &= \mathsf{5}\end{align}\)
b) \(\mathsf{x = -1}\)
\(\begin{align}\mathsf{f(-1)} &= \mathsf{2 \cdot (-1) + 1}\\ &= \mathsf{-2 + 1}\\ &= \mathsf{-1}\end{align}\)
Muuttujan arvo
Jos kysytään, millä muuttujan arvolla funktio saa tietyn arvon, tarvitaan yhtälönratkaisua.
Esimerkki: Millä muuttujan \(\mathsf{x}\) arvolla funktion \(\mathsf{f(x)=2x-1}\) arvo on \(\mathsf{3}\)?
Ratkaisu: Tiedetään, että \(\mathsf{f(x) = 3}\). Koska funktion arvot \(\mathsf{f(x)}\) saadaan lausekkeesta \(\mathsf{2x-1}\), voidaan merkitä:
\( \begin{align}\mathsf{f(x)} &= \mathsf{3} \\ \mathsf{2x-1} &= \mathsf{3} &&\mathsf{|| +1} \\ \mathsf{2x} &= \mathsf{4} &&\mathsf{|| : 2} \\ \mathsf{x} &= \mathsf{2}\end{align} \)
Vastaus: \(\mathsf{f(x) = 3}\) muuttujan arvolla \(\mathsf{x = 2}\).
3. Funktion kuvaaja
Funktion määrittämä sääntö voidaan esittää myös koordinaatistossa, jolloin sitä kutsutaan funktion kuvaajaksi. Kuvaaja koostuu pisteistä \(\mathsf{(x,y)}\), missä \(\mathsf{x}\) on muuttujan arvo, ja \(\mathsf{y}\) on funktion arvo, eli \(\mathsf{y = f(x)}\). Funktioita ja kuvaajia on lukemattomia erilaisia, mutta peruskoulussa keskitytään lineaarisiin funktioihin, joiden lausekkeet ovat 1. asteen polynomeja ja kuvaajat ovat suoria.
Lineaarisen funktion kuvaajan piirtäminen
Lineaarisen funktion kuvaajan eli suoran piirtämiseksi taulukoidaan vähintään kolme muuttujan arvoa, ja lasketaan niitä vastaavat funktion arvot.
Esimerkki: Piirrä funktion \(\mathsf{f(x) = 2x + 1}\) kuvaaja.
Paraabelin piirtäminen
Jos funktion lauseke on 2. asteen polynomi, sen kuvaaja ei ole suora vaan paraabeli. Paraabeli on käyrä, joten pisteitä kannattaa valita useita.
Esimerkki: Piirrä funktion \(\mathsf{g(x) = x^2}\) kuvaaja.
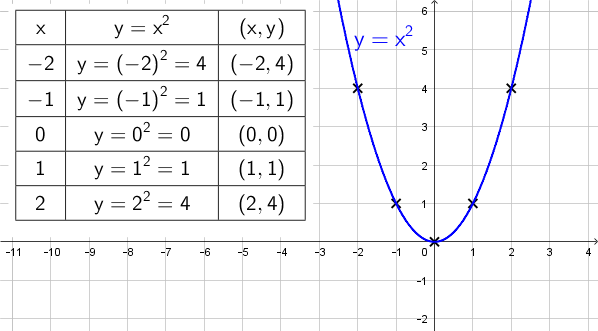
4. Suoran yhtälö
Suoran yhtälö on laskusääntö, jolla suoran pisteiden x-koordinaateista voidaan laskea niitä vastaavat y-koordinaatit (tai toisinpäin). Suoran yhtälö voidaan esittää monella tavalla, mutta peruskoulussa tutustutaan ns. ratkaistuun muotoon
\(\mathsf{y = \color{red}{k}x + \color{blue}{b}}\),
missä muuttujan x kerrointa \(\mathsf{\color{red}k}\) kutsutaan kulmakertoimeksi. Toista termiä \(\mathsf{\color{blue}b}\) kutsutaan tuttuun tapaan vakiotermiksi. Molemmilla käsitteillä on tärkeä ja havainnollinen rooli suoran sijainnissa koordinaatistossa. Alla olevassa taulukossa on esimerkkejä erilaisista suorien yhtälöistä, ja niiden kulmakertoimista ja vakiotermeistä.
| Suoran yhtälö | Kulmakerroin k | Vakiotermi b |
|---|---|---|
| \(\mathsf{y = {\color{red}2}x {\color{blue}+\:1}}\) | \(\mathsf{\color{red}2}\) | \(\mathsf{\color{blue}1}\) |
| \(\mathsf{y = {\color{red}-5}x {\color{blue}+\:5}}\) | \(\mathsf{\color{red}-5}\) | \(\mathsf{\color{blue}5}\) |
| \(\mathsf{y = {\color{red}3}x {\color{blue}-\:2}}\) | \(\mathsf{\color{red}3}\) | \(\mathsf{\color{blue}-2}\) |
| \(\mathsf{y = x \color{blue}+\:2}\) | \(\mathsf{\color{red}1}\) | \(\mathsf{\color{blue}2}\) |
| \(\mathsf{y = \color{blue}-3}\) | \(\mathsf{\color{red}0}\) | \(\mathsf{\color{blue}-3}\) |
| \(\mathsf{y = {\color{red}4}x}\) | \(\mathsf{\color{red}4}\) | \(\mathsf{\color{blue}0}\) |
Kulmakerroin
Kulmakerroin kertoo suoran kaltevuuden. Mittayksikkönä voidaan ajatella käytettävän y-akselin suuntaista muutosta, kun x-koordinaatin suuruus kasvaa yhdellä. Toisin sanoen, piirretään suoralle (mihin tahansa) piste, liikutaan yhden verran oikealle, ja lasketaan kuinka paljon tulee siirtyä ylös (tai alas), jotta päästään takaisin suoralle. Alla oleva kuva havainnollistaa kulmakertoimen \(\mathsf{k}\) määrittämistä suoran kuvaajasta.
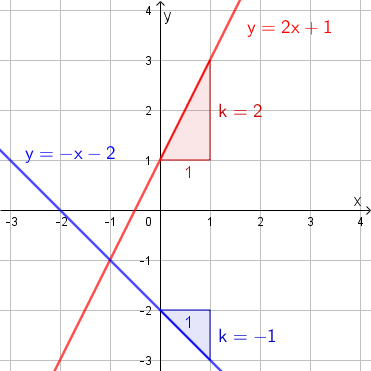
Tarkalleen ottaen kulmakerroin määritellään y-akselin suuntaisen siirtymän \(\mathsf{\Delta y}\) ja x-akselin suuntaisen siirtymän \(\mathsf{\Delta x}\) osamääränä. Alla olevasta kuvassa on esimerkkinä kulmakertoimen \(\textsf{k}\) määrittäminen tällä tavoin.
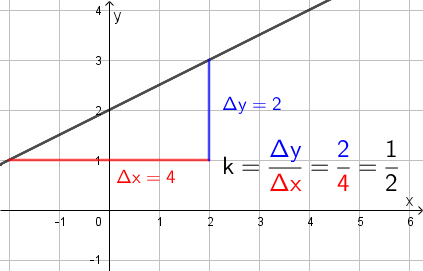
Jos kulmakerroin on positiivinen, sanotaan että suora on nouseva. Vastaavasti kulmakertoimen ollessa negatiivinen, suora on laskeva.
Vakiotermi
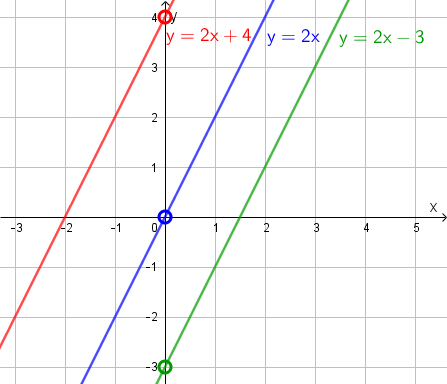
Vakiotermi kertoo suoran ja y-akselin leikkauskohdan. Toisin sanoen vakiotermi on suoran ja y-akselin leikkauspisteen y-koordinaatti, sillä x-koordinaattihan on tällöin aina 0. Vakiotermiä muuttamalla voidaan siis muuttaa suoran sijaintia y-akselin suunnassa. Alla olevassa kuvassa on esitetty yhdensuuntaisia suoria, joiden vakiotermi on eri.
5. Graafinen ja algebrallinen ratkaisu
Monia funktioiden kulkuun ja sijaintiin liittyviä ongelmia voidaan ratkaista sekä kuvaajasta katsomalla että ratkaisemalla yhtälöitä. Kuvaajasta katsomista kutsutaan graafiseksi ratkaisuksi, joka on erittäin hyvä menetelmä selvittää ratkaisu karkeasti. Graafisella ratkaisulla ei saada täysin tarkkoja vastauksia, mutta se helpottaa usein haastavien tehtävien ongelman rajaamista. Jos tehtävä ratkaistaan laskemalla tai ratkaisemalla yhtälö, sitä kutsutaan algebralliseksi ratkaisuksi. Algebrallisella ratkaisulla saadaan ratkaisuksi usein tarkka arvo tai ainakin riittävän tarkka likiarvo.
Funktion nollakohta
Funktion nollakohta eli juuri tarkoittaa muuttujan arvoa, jolla funktion arvo on nolla. Nollakohtia voi olla yksi, useampi tai ei yhtään. Funktion nollakohtien ratkaiseminen on suuressa roolissa peruskoulun jälkeisissä opinnoissa, kun funktioita aletaan analysoida tarkemmin. Se antaa myöskin uuden työkalun vaikeampien yhtälöiden ja funktoiden ratkaisemiseen, jolloin ongelmaa voidaan rajata nollakohtien avulla. Peruskoulussa funktion nollakohdan ratkaiseminen toimii monipuolisena harjoituksena ja vahvistaa ymmärrystä opiskeltavasta asiasta.
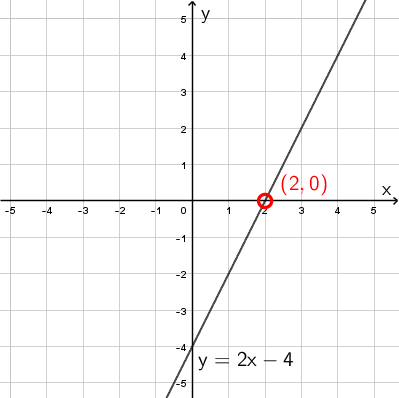
Esimerkki: Ratkaise funktion \(\mathsf{f(x) = 2x - 4}\) nollakohta.
Graafinen ratkaisu: Piirretään funktion kuvaaja, ja etsitään kuvaajan ja x-akselin leikkauskohta.
Algebrallinen ratkaisu: Etsitään muuttujan x arvo, jolla funktio saa arvon 0, eli muodostetaan ja ratkaistaan yhtälö \(\mathsf{f(x) = 0}\).
\(\begin{align}\mathsf{f(x)} &= \mathsf{0}\\ \mathsf{2x-4} &= \mathsf{0} &&\mathsf{\| +4}\\ \mathsf{2x} &= \mathsf{4} &&\mathsf{\| :2}\\ \mathsf{x} &= \mathsf{2}\end{align}\)
Vastaus: Funktion nollakohta on x = 2.
Piste kuvaajalla
"Onko piste funktion kuvaajalla?" -tehtävä voidaan ajatella myös muodossa "Toteuttaako lukupari funktion säännön?" Tätä tietoa voidaan käyttää esimerkiksi funktion säännön tutkimisessa, monimutkaisten funktioiden analysoinnissa tai tietokonegrafiikassa valonsäteiden mallinnuksessa.
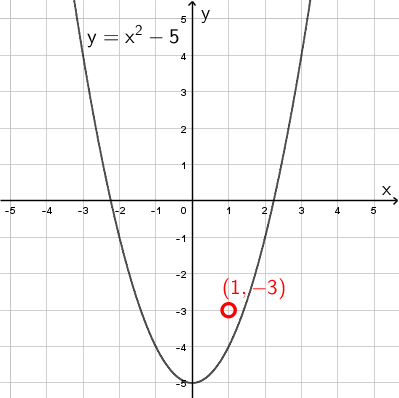
Esimerkki: Onko piste \(\mathsf{(1, -3)}\) funktion \(\mathsf{f(x)=x^2-5}\) kuvaajalla?
Graafinen ratkaisu: Piirretään funktion kuvaaja ja piste samaan koordinaatistoon, ja katsotaan onko piste kuvaajalla.
Algebrallinen ratkaisu: Lasketaan funktion arvo pisteen x-koordinaatin arvolla ja verrataan funktion arvo y-koordinaatin arvoon.
\(\begin{align}\mathsf{f(x)} &= \mathsf{x^2-5}\\ \mathsf{f(1)} &= \mathsf{1^2-5}\\ &= \mathsf{1-5}\\ &= \mathsf{-4}\end{align}\)
Vastaus: Piste (1, -3) ei ole funktion f kuvaajalla.
Kuvaajien leikkauspiste
Kuvaajien leikkaupisteen etsiminen voidaan ajatella graafisena yhtälön ratkaisemisena. Yhtälön molempien puolien lausekkeet piirretään koordinaatistoon ja leikkauspisteen x-koordinaatti on yhtälön ratkaisu. Toisaalta leikkauspisteen y-koordinaatti kertoo leikkauspisteestä saatavan yhteisen funktion arvon. Myöhemmin 9. luokalla tätä menetelmää käytetään yhtälöparien ratkaisemiseen. Muistutuksena jälleen, että graafinen ratkaisu antaa usein epätarkan arvon, jonka avulla voidaan toki tarkistalla algebrallisella menetelmällä saadun ratkaisun järkevyyttä.
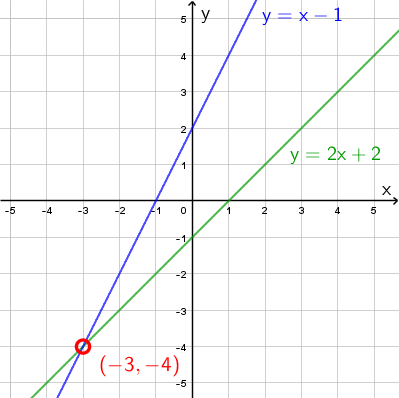
Esimerkki: Missä pisteessä funktioiden \(\mathsf{f(x)=2x+2}\) ja \(\mathsf{g(x)=x-1}\) kuvaajat leikkaavat toisensa?
Graafinen ratkaisu: Piirretään funktioiden kuvaajat samaan koordinaatistoon, ja katsotaan missä pisteessä kuvaajat leikkavat.
Algebrallinen ratkaisu: Merkitään funktioiden lausekkeet yhtä suuriksi ja ratkaistaan muodostuneesta yhtälöstä x. Ratkaistaan leikkauspisteen y-koordinaatti tämän jälkeen laskemalla toisen funktion arvo saadulla muuttujan x arvolla.
Ratkaistaan x-koordinaatti:
\(\begin{align}\mathsf{f(x)} &= \mathsf{g(x)}\\ \mathsf{2x+2} &= \mathsf{x-1} &\|\mathsf{-x}\\ \mathsf{x+2} &= \mathsf{-1} &\|\mathsf{-2}\\ \mathsf{x}&= \mathsf{-3}\end{align}\)
Ratkaistaan y-koordinaatti:
\(\mathsf{y = g(-3) = -3-1 = -4}\)
Vastaus: Funktiot leikkaavat pisteessä \(\mathsf{(-3,-4)}\).