MA8 Jakso 6: Ympyrä
1. Ympyrän osat ja luku π
Pyörä on ollut kiistämättä tärkeä keksintö ihmiskunnan historiassa. Ympyrä liittyy kuitenkin pyöreän muodon lisäksi kaikenlaiseen pyörivään liikkeeseen, joten ympyrään liittyvien perusasioiden ymmärtäminen on tärkeää.
7. luokalla tutustuttiin ympyrän osiin, ja harjoiteltiin sen piirtämistä harpin avulla. Harppia käytettiin myös geometrisessa piirtämisessä, kun piirrettiin esimerkiksi normaaleja ja kulmanpuolittajia. 8. luokalla opitaan ympyrän kehän pituuden ja pinta-alan laskeminen säteen avulla sekä vastaavat suureet myös ympyrän osalle eli sektorille. 9. luokalla ympyrää käytetään pohjana monenlaisille kappaleille (ympyrälieriö, ympyräkartio,...) ja pyöräytetään ympyrä palloksi.
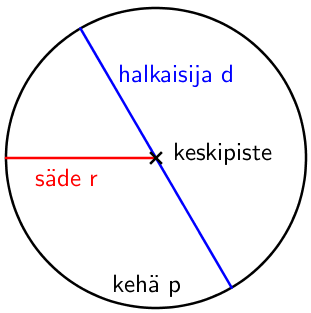
Ympyrän osat
Ympyrä muodostuu keskipisteestä, ja siitä tietyn säteen etäisyydellä olevista kehän pisteistä. Jänne on jana, joka yhdistää kaksi kehän pistettä. Jänne, joka kulkee keskipisteen kautta on nimeltään halkaisija. Halkaisijan voidaan ajatella olevan kaksi perättäistä sädettä. Näin ollen säde on helppo laskea, jos tunnetaan halkaisija ja päin vastoin.
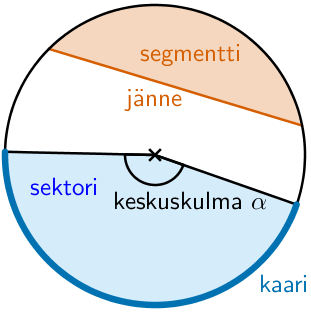
Kahden säteen rajaamaa aluetta kutsutaan sektoriksi. Sektori rajaa ympyrän kehältä kaaren, joka on siis kehän osa. Säteiden välistä kulmaa kutsutaan keskuskulmaksi, koska sen kärki on ympyrän keskipisteessä. Sektorista tarkemmin luvussa 4. Sektori.
Ympyrän piirtäminen
Ympyrän piirtäminen voidaan jakaa seuraaviin viiteen vaiheeseen:
- Piirrä keskipiste.
- Aseta harpin piikki keskipisteeseen
- Mittaa harpin leveydeksi haluttu säde.
- Piirrä ympyrä.
- Pidä piikki paikallaan, ja liikuta kynää. Älä päästä sädettä muuttumaan. Tämä vaatii harjoittelua.
- Piirrä ja merkitse lopuksi tehtävänannossa annettu pituus (säde tai halkaisija) näkyviin.
Luku π
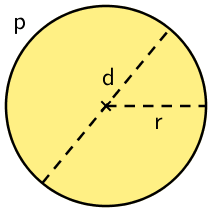
Ympyrän kehän \(\mathsf{p}\) ja halkaisijan \(\mathsf{d}\) suhde on kaikissa ympyröissä sama. Tätä vakiota merkitään kreikkalaisten aakkosten pienellä pii (\(\pi\))-kirjaimella.
\(\mathsf{\dfrac{p}{d} = 3,\!14159265... = \pi}\)
Pii kirjoitetaan kuin T-kirjain kahdella "jalalla", mutta hieman pienempänä. Päällä oleva vaakasuora viiva voi olla myös aaltomainen.

Piin likiarvo löytyy laskimista, mutta suuruus on hyvä muistaa ulkoa kahden desimaalin tarkkuudella.
\(\mathsf{\pi \approx 3,\!14}\)
Lisätietoa: Hieman piin likiarvon historiasta
Ympyrän kehän ja halkaisijan välisen suhteen säännönmukaisuus on tunnettu jo tuhansia vuosia. Ainakin muinaiset egyptiläiset käyttivät Rhindin papyruksen (n. 1600 eaa.) tehtävässä piille likiarvoa \(\mathsf{\dfrac{256}{81} = 3,\!16...}\). Babylonialaiset käyttivät yleisesti kehän ja halkaisijan suhteelle likiarvoa \(\mathsf{3}\) tai \(\mathsf{3\frac{1}{8}}\). Myöhemmin Arkhimedes (n. 250 eaa.) sai yksinkertaistettua likiarvon välille \(\mathsf{3\frac{10}{71} < \pi < 3\frac{1}{7}}\). Vanha testamentti pitää sisällään laskuesimerkin, jonka mukaan π:n likiarvo on kolme.
”Hiram valoi myös pyöreän altaan, jota kutsuttiin mereksi. Se oli reunasta reunaan kymmenen kyynärän levyinen, korkeutta sillä oli viisi kyynärää, ja vasta kolmenkymmenen kyynärän pituinen mittanuora ulottui sen ympäri”
Ajanlaskun alun jälkeen piin likiarvolle on pyritty laskemaan mahdollisimman tarkkaa arvoa ympäri maailman eri kulttuurien matematiikassa. Kiinassa Zu Chongzhi (430 - 501) pääsi tulokseen \(\mathsf{3,\!1415926 < \pi < 3,\!1415927}\). Islamilaisessa matematiikassa Al-Kashi laski piille 16-desimaalisen likiarvon 1400-luvun alkupuoliskolla.
Likiarvojen laskeminen perustuu erilaisten sarjakehitelmien käyttöön. Ennen tietokoneiden laskentatehoa desimaalit oli laskettava käsin. Nykyisin piin likiarvosta tunnetaan kymmeniä biljoonia desimaaleja.
2. Ympyrän kehä
Tässä luvussa opittavat laskukaavat:
Ympyrän kehän pituuden laskeminen
Ympyrän kehän pituuden (ympärysmitta, piiri) laskemisessa hyödynnetään edellisessä luvussa opittua tietoa, että ympyrän kehän pituuden (\(\mathsf{p}\)) ja halkaisijan (\(\mathsf{d}\)) välinen suhde on vakio.
\(\mathsf{\dfrac{p}{d} = \pi}\)
Kertomalla yhtälö puolittain halkaisijalla (\(\mathsf{d}\)) saadaan laskukaava ympyrän kehän pituudelle.
\(\begin{align}\mathsf{\dfrac{p}{d}} &= \mathsf{\pi \qquad \| \cdot d}\\\mathsf{p} &= \mathsf{\pi \cdot d}\\\mathsf{p} &= \mathsf{\pi d}\end{align}\)
Ympyrän kehän pituus voidaan siis laskea, jos tunnetaan sen halkaisija. Vanhastaan tiedetään myös, että ympyrän halkaisija on kaksinkertainen sen säteeseen (\(\mathsf{r}\)) verrattuna, eli \(\mathsf{d = 2 \cdot r}\). Kehän pituuden laskukaava voidaan siis muokata muotoon
\(\begin{align}\mathsf{p} &= \mathsf{2 \cdot \pi \cdot r}\\\mathsf{p} &= \mathsf{2 \pi r}\end{align}\).
Esimerkki: Laske ympyrän kehän pituus.
a)
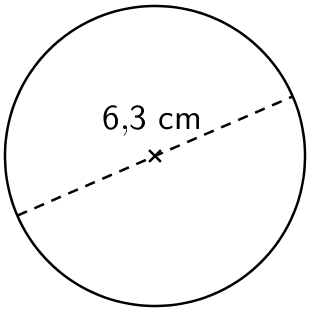
\(\begin{align}\mathsf{p}&= \mathsf{\pi \cdot d}\\ &= \mathsf{\pi \cdot 6,\!3}\\ &= \mathsf{19,\!79...}\\ &\approx \mathsf{20}\end{align}\)
Vastaus: Ympyrän kehän pituus on 20 cm.
b)
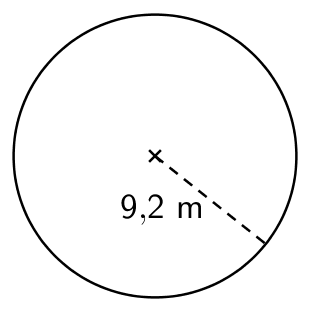
\(\begin{align}\mathsf{p}&= \mathsf{2 \cdot \pi \cdot r}\\ &= \mathsf{2 \cdot \pi \cdot 9,\!2}\\ &= \mathsf{57,\!80...}\\ &\approx \mathsf{58}\end{align}\)
Vastaus: Ympyrän kehän pituus on 58 m.
Käänteisiä tilanteita
Laskukaavoja on hyödyllistä osata käyttää myös käänteisesti. Pyöreiden kappaleiden ympärysmitta eli ympyrän kehän pituus on usein helpompi selvittää esimerkiksi mittaamalla kuin esimerkiksi säde. Yksi tapa ratkaista käänteinen ongelma on sijoittaa tunnettuun laskukaavaan tunnentut arvot ja ratkaista yhtälönratkaisun menetelmillä tuntematon arvo.
Esimerkki: Laske ympyrän säteen pituus.
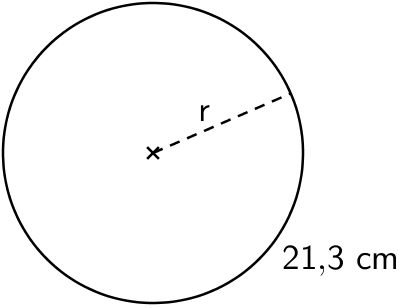
\(\begin{align}\mathsf{p} &= \mathsf{2\cdot \pi \cdot r}\\ \textsf{21,3 cm} &= \mathsf{2 \cdot \pi \cdot r} \qquad &&\|:\mathsf{2}\\ \textsf{10,65 cm} &= \mathsf{\pi \cdot r} \qquad &&\|:\mathsf{\pi}\\ \textsf{3,390... cm} &= \mathsf{r}\\ \mathsf{r} &\approx \textsf{3,39 cm}\end{align}\)
\(\begin{align}\mathsf{p} &= \mathsf{2\pi r}\\ \textsf{21,3 cm} &= \mathsf{2\pi r} \qquad &&\|:\mathsf{2\pi}\\ \textsf{3,390... cm} &= \mathsf{r}\\ \mathsf{r} &\approx \textsf{3,39 cm}\end{align}\)
Vastaus: Ympyrän säteen pituus on 3,39 cm.
.Toinen tapa on muokata alkuperäisiä laskukaavoja siten, että niiden avulla voidaan laskea haluttu suure.
Kehän pituudesta halkaisija
\(\begin{align}\mathsf{p} &= \mathsf{\pi \cdot d \quad \| : \pi}\\\\ \mathsf{\dfrac{p}{\pi}} &= \mathsf{d}\\ \mathsf{d} &= \mathsf{\frac{p}{\pi}}\\ \phantom{\mathsf{r}} &\phantom{= \mathsf{\dfrac{p}{2 \cdot \pi}}}\end{align}\)
Kehän pituudesta säde
\(\begin{align}\mathsf{p} &= \mathsf{2 \cdot \pi \cdot r \quad} &\mathsf{\| : \pi}\\\\ \mathsf{\dfrac{p}{\pi}} &= \mathsf{2 \cdot r} &\mathsf{\| : 2}\\ \mathsf{\dfrac{p}{2 \cdot \pi}} &= \mathsf{r}\\ \mathsf{r} &= \mathsf{\dfrac{p}{2 \cdot \pi}}\end{align}\)
Esimerkki: Laske ympyrän halkaisijan pituus.
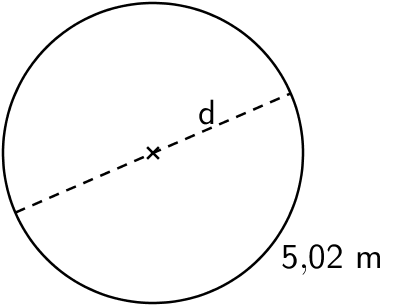
\(\begin{align}\mathsf{d}&= \mathsf{\dfrac{p}{\pi}}\\ &= \mathsf{\dfrac{5,\!02}{\pi}}\\ &= \mathsf{1,\!597...}\\ &\approx \mathsf{1,\!60}\end{align}\)
Vastaus: Ympyrän halkaisijan pituus on 1,60 m.
3. Ympyrän pinta-ala
Tässä luvussa opittavat laskukaavat:

Ympyrän pinta-alan laskeminen
Ympyrän (tai tarkemmin ympyrän sisään jäävän alueen) pinta-alan laskeminen tapahtuu kertomalla pii (\(\pi\)) ympyrän säteen neliöllä (\(\mathsf{r^2}\)).
\(\begin{align}\mathsf{A} &= \mathsf{\pi\cdot r^2}\\\mathsf{A} &= \mathsf{\pi r^2}\end{align}\)
Jos ympyrästä tunnetaan säteen sijaan halkaisia, saadaan säde puolittamalla halkaisija, sillä \(\mathsf{r = \dfrac{d}{2}}\).
Esimerkki: Laske ympyrän pinta-ala.
a)
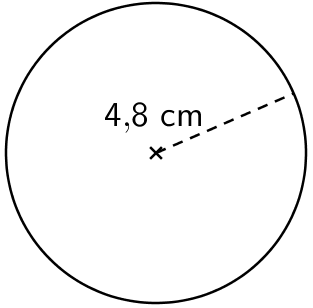
\(\begin{align}\mathsf{A}&= \mathsf{\pi \cdot r^2}\\ &= \mathsf{\pi \cdot 4,\!8^2}\\ &= \mathsf{72,\!38...}\\ &\approx \mathsf{72}\end{align}\)
Vastaus: Ympyrän pinta-ala on 72 cm².
b)
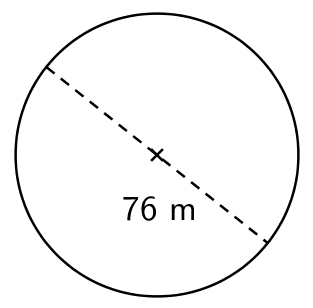
\(\begin{align}\mathsf{r} &= \mathsf{\dfrac{d}{2} = \dfrac{76}{2}= 38}\\\\ \mathsf{A}&= \mathsf{\pi \cdot r^2}\\ &= \mathsf{\pi \cdot 38^2}\\ &= \mathsf{4\,536,4...}\\ &\approx \mathsf{4\,500}\end{align}\)
Vastaus: Ympyrän pinta-ala on 4 500 m².
Eräs tapa ympyrän pinta-alan laskukaavan johdatteluun on ajatusmalli, jossa ympyrä "kuoritaan" sipulin kaltaisesti ja tarkastellaan kuorten muodostamaa pintaa. Muitakin yläkouluun sopivia johdantoja on paljon, mutta varsinainen pinta-alan kaavan johtaminen jätetään myöhempiin opintoihin. Alla olevassa demonstraatiossa on esitetty vaiheittain sipulimalli ympyrän pinta-alan johtamiseksi.
Käänteisiä tilanteita
Ympyrän pinta-alan kaavan avulla voidaan laskea myös ympyrän säde, jos pinta-ala tunnetaan. Tämä voidaan tehdä jälleen kahdella tavalla: sijoittamalla pinta-alan arvo kaavaan ja ratkaisemalla yhtälö tai muokkaamalla ensin laskukaava säteelle.
Esimerkki: Laske ympyrän säteen pituus.
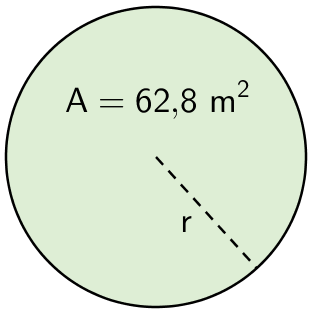
\(\begin{align}\mathsf{A}&= \mathsf{\pi r^2}\\ \textsf{62,8} &= \mathsf{\pi r^2} \qquad &&\|:\pi\\ \textsf{19,98...} &= \mathsf{r^2} &&\|\sqrt{\quad}\\ \textsf{4,471...} &= \mathsf{r}\\ \mathsf{r} &\approx \textsf{4,47}\end{align}\)
Vastaus: Ympyrän säteen pituus on 4,47 m.
Johdetaan laskukaava ympyrän säteelle, kun ympyrästä tunnetaan pinta-ala. Ratkaistaan siis pinta-alan yhtälöstä (laskukaavasta) säde r.
\(\begin{align}\mathsf{A} &= \mathsf{\pi \cdot r^2} \quad && \| : \pi\\ \mathsf{\dfrac{A}{\pi}} &= \mathsf{r^2} && \|\sqrt{\quad}\\ \mathsf{\sqrt{\dfrac{A}{\pi}}} &= \mathsf{r}\\ \mathsf{r} &= \mathsf{\sqrt{\dfrac{A}{\pi}}}\end{align}\)
Esimerkki: Laske ympyrän säteen pituus.

\(\begin{align}\mathsf{r}&= \mathsf{\sqrt{\dfrac{A}{\pi}}}\\ &= \mathsf{\sqrt{\dfrac{62,\!8}{\pi}}}\\ &= \mathsf{4,\!471...}\\ &\approx \mathsf{4,\!47}\end{align}\)
Vastaus: Ympyrän säteen pituus on 4,47 m.
4. Sektori
Tässä luvussa opittavat laskukaavat:
Kaaren pituus:
\(\mathsf{b} = \mathsf{\dfrac{\alpha}{360^\circ} \cdot 2 \pi r}\)
Pinta-ala:
\(\mathsf{A_s} = \mathsf{\dfrac{\alpha}{360^\circ} \cdot \pi r^2}\)
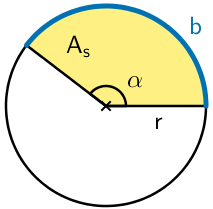
Sektori ympyrän osana
Kun ympyrästä rajataan kahden säteen avulla osa, sitä kutsutaan sektoriksi. Sektorin pinta-ala voidaan laskea osana koko ympyrän pinta-alasta. Vastaavasti sektorin kaaren pituus voidaan laskea osana kokonaisen ympyrän kehän pituudesta.
Esimerkki: Ympyrän säde on 6,7 cm. Ympyrästä leikataan sektori. Laske sektorin kaaren pituus ja pinta-ala, kun sektori on kokonaisen ympyrän
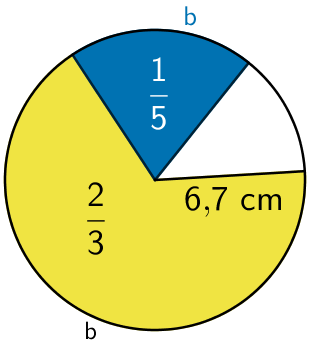
a) viideosa (sininen)
Kaaren pituus
\(\begin{align}\mathsf{b} &= \mathsf{\dfrac{1}{5} \cdot 2\pi r}\\&= \mathsf{\dfrac{1}{5} \cdot 2 \cdot \pi \cdot 6,\!7}\\&= \mathsf{8,\!419...}\\&\approx \mathsf{8,4}\end{align}\)
Vastaus: Sektorin kaaren pituus on 8,4 cm.
Pinta-ala
\(\begin{align}\mathsf{A_s} &= \mathsf{\dfrac{1}{5} \cdot \pi r^2}\\&= \mathsf{\dfrac{1}{5} \cdot \pi \cdot 6,\!7^2}\\&= \mathsf{28,\!20...}\\&\approx \mathsf{28}\end{align}\)
Vastaus: Sektorin pinta-ala on 28 cm2.
b) kaksi kolmasosaa (keltainen)
Kaaren pituus:
\(\begin{align}\mathsf{b} &= \mathsf{\dfrac{2}{3} \cdot 2\pi r}\\&= \mathsf{\dfrac{2}{3} \cdot 2 \cdot \pi \cdot 6,\!7}\\&= \mathsf{28,\!06...}\\&\approx \mathsf{28}\end{align}\)
Vastaus: Sektorin kaaren pituus on 28 cm.
Pinta-ala
\(\begin{align}\mathsf{A_s} &= \mathsf{\dfrac{2}{3} \cdot \pi r^2}\\&= \mathsf{\dfrac{2}{3} \cdot \pi \cdot 6,\!7^2}\\&= \mathsf{94,\!01...}\\&\approx \mathsf{94}\end{align}\)
Vastaus: Sektorin pinta-ala on 94 cm2.
Sektori keskuskulman avulla
Sektoria vastaavan osan suuruus voidaan ilmoittaa myös keskuskulman avulla. Keskuskulman suuruus suhteessa kokonaiseen ympyrään (\(\mathsf{360^\circ}\)) kertoo murto-osan, joka otetaan koko ympyrän kehän pituudesta tai pinta-alasta.
Esimerkki: Laske sektorin kaaren pituus ja pinta-ala.
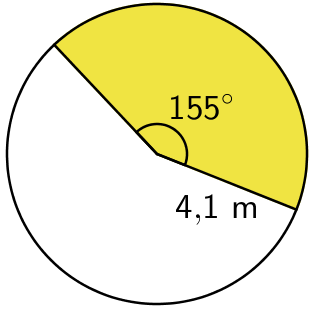
Kaaren pituus:
\(\begin{align}\mathsf{b} &= \mathsf{\dfrac{\alpha}{360^\circ} \cdot 2\pi r}\\&= \mathsf{\dfrac{155^\circ}{360^\circ} \cdot 2 \cdot \pi \cdot 4,\!1}\\&= \mathsf{11,\!09...}\\&\approx \mathsf{11}\end{align}\)
Vastaus: Sektorin kaaren pituus on 11 m.
Pinta-ala:
\(\begin{align}\mathsf{A_s} &= \mathsf{\dfrac{\alpha}{360^\circ} \cdot \pi r^2}\\&= \mathsf{\dfrac{155^\circ}{360} \cdot \pi \cdot 4,\!1^2}\\&= \mathsf{22,\!73...}\\&\approx \mathsf{23}\end{align}\)
Vastaus: Sektorin pinta-ala on 23 m2.