MA8 Jakso 5: Pythagoraan lause
1. Kertausta
Pituusyksiköt
Pituuden perusyksikkö on metri, ja se lyhennetään pienellä \(\textsf{m}\)-kirjaimella. Pienempiä ja suurempia pituusyksiköitä saadaan kertomalla tai jakamalla luvulla 10, ja käyttämällä määrättyjä etuliitteitä, kuten milli-, sentti- tai kilo. Perusyksikköä metri lähimmät pituusyksiköt lyhenteineen on esitetty alla olevassa taulukossa.
| km | hm | dam | m | dm | cm | mm |
|---|---|---|---|---|---|---|
| kilometri | hehtometri | dekametri | metri | desimetri | senttimetri | millimetri |
| 1000 m | 100 m | 10 m | 1 m | 0,1 m | 0,01 m | 0,001 m |
Kun pituus muutetaan pienempään yksikköön, lukua kerrotaan 10:llä, eli pilkku siirtyy oikealle.
Esimerkki: Muunna suluissa annettuun yksikköön.
a) \(\textsf{8 cm (mm)}\)
\(\textsf{8 cm = 80 mm}\)

Pilkku siirtyy oikealle yhden numeron yli.
b) \(\textsf{6,4 m (cm)}\)
\(\textsf{6,4 m = 640 cm}\)
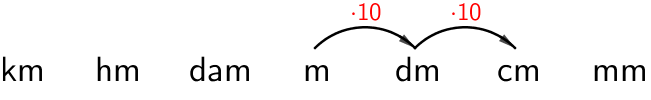
Pilkku siirtyy oikealle kahden numeron yli.
c) \(\textsf{0,2 km (m)}\)
\(\textsf{0,2 km = 200 m}\)

Pilkku siirtyy oikealle kolmen numeron yli.
Kun muutetaan suurempaan yksikköön, luku vastaavasti jaetaan 10:llä, eli pilkku siirtyy vasemmalle.
Esimerkki: Muuta suluissa annettuun yksikköön.
a) \(\textsf{2500 dm (m)}\)
\(\textsf{2500 dm = 250 m}\)
Pilkku siirtyy vasemalle yhden numeron yli.
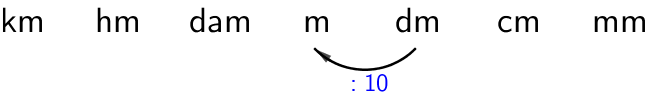
b) \(\textsf{140 dam (km)}\)
\(\textsf{140 dam = 1,4 km}\)
Pilkku siirtyy vasemmalle kahden numeron yli.
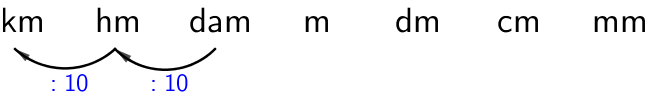
c) \(\textsf{952 mm (m)}\)
\(\textsf{952 mm = 0,952 m}\)
Pilkku siirtyy vasemmalle kolmen numeron yli.
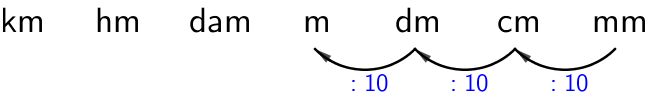
Pinta-alayksiköt
Pinta-alan perusyksikkö on neliömetri, ja se lyhennetään \(\mathsf{m^2}\)-merkinnällä (\(\mathsf{1\:m \cdot 1\:m = 1\:m^2}\)). Pienempiä ja suurempia pinta-alayksiköitä saadaan kertomalla tai jakamalla luvulla 100, ja käyttämällä määrättyjä etuliitteitä, kuten pituusyksiköissä. Poikkeuksena on neliöhehtometri eli hehtaari sekä neliödekametri eli aari. Tärkeimmät pinta-alayksiköt lyhenteineen on esitetty alla olevassa taulukossa.
| km2 | ha | a | m2 | dm2 | cm2 | mm2 |
|---|---|---|---|---|---|---|
| neliökilometri | hehtaari | aari | neliömetri | neliödesimetri | neliösenttimetri | neliömillimetri |
| 1 000 000 m2 | 10 000 m2 | 100 m2 | 1 m2 | 0,01 m2 | 0,0001 m2 | 0,000001 m2 |
Kun siirrytään pienempiin yksiköihin, niin jokaisessa vaiheessa kerrotaan luvulla 100.
Esimerkki: Muuta suluissa annettuun yksikköön.
a) \(\mathsf{\textsf{8 cm}^2\;(\textsf{mm}^2})\)
\(\mathsf{\textsf{8 cm}^2 = \textsf{800 mm}^2}\)
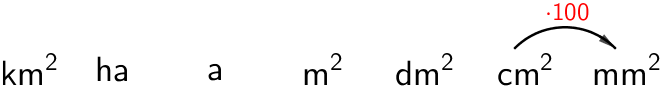
Pilkku siirtyy oikealle kahden numeron yli.
b) \(\mathsf{\textsf{6,4 m}^2\;(\textsf{cm}^2})\)
\(\mathsf{\textsf{6,4 m}^2 = \textsf{64 000 cm}^2}\)
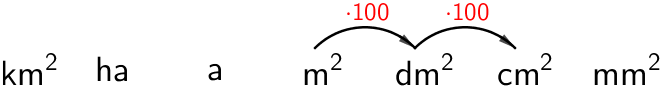
Pilkku siirtyy oikealle neljän numeron yli.
c) \(\mathsf{\textsf{0,2 km}^2\;(\textsf{m}^2})\)
\(\mathsf{\textsf{0,2 km}^2 = \textsf{20 000 m}^2}\)

Pilkku siirtyy oikealle kuuden numeron yli.
Kun muutetaan suurempaan yksikköön, luku vastaavasti jaetaan 100:lla.
Esimerkki: Muuta suluissa annettuun yksikköön.
a) \(\mathsf{\textsf{2500 dm}^2\;(\textsf{m}^2})\)
\(\mathsf{\textsf{2500 dm}^2 = \textsf{25 m}^2}\)
Pilkku siirtyy vasemmalle kahden numeron yli.
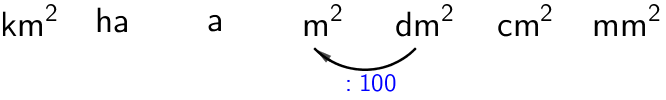
b) \(\mathsf{\textsf{1 400 a}\;(\textsf{km}^2})\)
\(\mathsf{\textsf{1 400 a} = \textsf{0,14 km}^2}\)
Pilkku siirtyy vasemmlle neljän numeron yli.
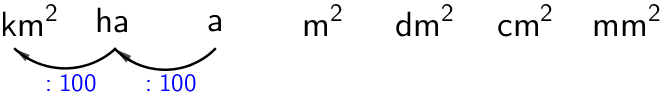
c) \(\mathsf{\textsf{2 195 000 mm}^2\;(\textsf{m}^2})\)
\(\mathsf{\textsf{2 195 000 mm}^2 = \textsf{2,195 m}^2}\)
Pilkku siirtyy vasemmalle kuuden numeron yli.
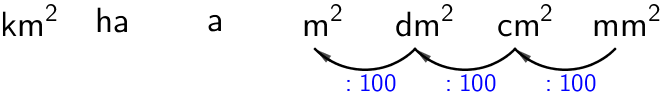
Piiri
Monikulmiosta voidaan laskea piiri, joka on sen sivujen summa. Piiriä merkitään muuttujalla \(\textsf{p}\).
Esimerkki: Laske monikulmion ABCD piiri.
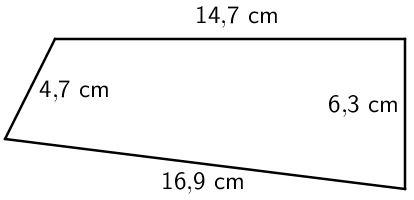
\(\begin{align}\textsf{p} &= \textsf{16,9 cm + 6,3 cm + 14,7 cm + 4,7 cm}\\ &=\textsf{42,6 cm}\end{align}\)
Pinta-ala
Pinta-ala kuvaa kaksiulotteisen kuvion suuruutta. Suorakulmion pinta-alan muistamalla pääsee jo melko pitkälle geometrian tehtävissä. Jakson aihe liittyy suorakulmaisiin kolmioihin, joten on järkevää kerrata kolmion pinta-alan laskukaava sekä hyödyllisenä kertauksena myös puolisuunnikkaan pinta-alan laskeminen.
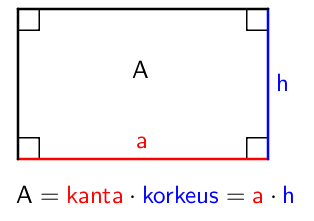
Suorakulmion pinta-ala
Suorakulmion (ja neliön) pinta-ala on kaikkein selkein pinta-ala laskettavaksi. Pinta-alan laskemista varten suorakulmiosta tulee tuntea sen kanta (leveys) ja korkeus. Suorakulmion pinta-ala on kannan ja korkeuden tulo.
Esimerkki: Laske suorakulmion pinta-ala.
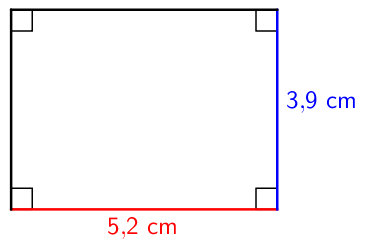
\(\mathsf{A = \text{5,2 cm} \cdot \text{3,9 cm} = \text{20,29 cm}^2}\)
Kolmion pinta-ala
Kolmion pinta-alaa laskettaessa tarvitaan suorakulmion tapaan kolmion leveys (kanta) ja korkeus. Leveydeksi eli kannaksi valitaan jokin kolmion sivu, jolloin korkeus on kannan ja kolmannen kärkipisteen välinen kohtisuora etäisyys. Pinta-ala \(\textsf{A}\) lasketaan kertomalla kanta \(\textsf{a}\) ja korkeus \(\textsf{h}\) keskenään, ja jakamalla saatu tulo kahdella. Jos kahdella jakaminen hämmentää, kannattaa tutustua nelikulmioiden pinta-alan laskemiseen, jolloin havaitaan kolmion olevan aina jonkin nelikulmion (suunnikkaan) puolikas.
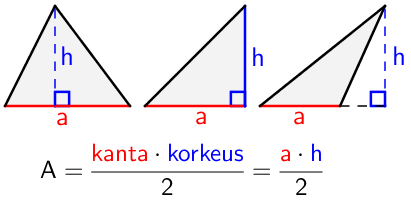
Kun kolmion korkeus merkitään näkyviin, sitä kutsutaan korkeusjanaksi. Suorakulmaisella kolmiolla kannaksi ja korkeudeksi kannattaa valita kohtisuorat sivut. Tylppäkulmaisen kolmion tapauksessa korkeusjana voi tulla kolmion ulkopuolelle, jolloin se on kohtisuorassa kannalle piirretyn jatkeen kanssa.
Esimerkki: Laske kolmion pinta-ala.
Suunnikkaan pinta-ala
Suunnikkaan pinta-alan laskemista voidaan lähestyä kahdella eri tavalla. Ensiksi, suunnikas voidaan jakaa kahdeksi yhteneväksi (yhtä suureksi) kolmioksi, joiden pinta-alat selvittämällä ja yhteen laskemalla saadaan suunnikkaan pinta-ala. Toisaalta, suunnikas voidaan ajatella suorakulmioksi, jonka yksi kulma on siirtynyt kuvion toiselle puolelle. Tästä voidaan päätellä, että pinta-ala lasketaan kuten vastaavan suorakulmionkin, eli kannan ja korkeuden tulona.
Esimerkki: Laske suunnikkaan pinta-ala.
Pyöristäminen
Desimaalilukujen pyöristämistä käsiteltiin 7. luokalla, ja siihen liittyviä käytäntöjä on hyvä kerrata varsinkin geometrian yhteydessä, kun käsitellään mitattuja epätarkkoja arvoja. Pyöristystarkkuuteen vaikuttaa mittaustarkkuuden lisäksi laskutoimitukset, joita "epätarkoilla" arvoilla lasketaan. Vastausta ei voi, eikä kannata antaa liian tarkasti. Tässä vaiheessa ei paneuduta sen tarkemmin mittausvirheen määrittämiseen, vaan todetaan hyvät yleiskäytännöt summan ja erotuksen sekä tulon ja osamäärän pyöristämiseen.
Desimaalilukujen tapauksessa pyöristäminen tulee ajankohtaiseksi paljon useammin kuin kokonaislukujen tapauksessa. Usein esimerkiksi jakolasku ei mene tasan, ja vastauksena voi olla päättymätön desimaaliluku, joka pitäisi pyöristää järkevään tarkkuuteen. Pyöristyksessä tarkkuus voidaan esittää kolmella eri tavalla:
- Numeron paikan perusteella
- Desimaalien lukumäärän perusteella (summa ja erotus)
- Merkitsevien numeroiden perusteella (tulo ja osamäärä)
Valittu tarkkuus määritellään sen mukaan, mistä laskutoimituksesta tai mittalaitteesta pyöristettävä desimaaliluku on peräisin. Epätarkin lähtöarvo määrittää aina pyöristyksen tarkkuuden.
Pyöristäminen paikan perusteella
Esimerkiksi sadasosien tarkkuuteen pyöristettäessä pyöristysraja tulee siis sadasosia kuvaavan numeron perään.
Esimerkki: Pyöristä luku 3,1415
a) kokonaisten tarkkuuteen
\( \mathsf{\text{3,} {\color{red}|}\text{1415} \approx \text{3}} \)
b) sadasosien tarkkuuteen
\( \mathsf{\text{3,14} {\color{red}|}\text{15} \approx \text{3,14}} \)
c) tuhannesosien tarkkuuteen.
\( \mathsf{\text{3,141} {\color{red}|}\text{5} \approx \text{3,142}} \)
Pyöristyksen tapahtuessa desimaaliosan puolella, pyöristettyjä desimaaleja ei korvata nollilla, vaan viimeinen numero (oikealla) kuvaa pyöristetyn luvun tarkkuuttaa, ja sen on oltava sama kuin haluttu tarkkuus.
Pyöristäminen desimaalien perusteella
Yhteen- ja vähennyslaskujen vastausta pyöristettäessä tutkitaan lähtöarvojen desimaalien lukumäärää, jonka perusteella vastauskin pyöristetään. Tästä tarkemmin alempana. Tarkkuuden ilmoittamiseen desimaalien lukumäärä on selkeä.
Esimerkki: Pyöristä luku 9,5297
a) kolmen desimaalin tarkkuuteen
\( \mathsf{\text{9,529}{\color{red}|}\text{7} \approx \text{9,530}} \)
b) yhden desimaalin tarkkuuteen
\( \mathsf{\text{9,5}{\color{red}|}\text{297} \approx \text{9,5}} \)
c) kokonaisten tarkkuuteen
\( \mathsf{\text{9,}{\color{red}|}\text{5297} \approx \text{10}} \)
Jos lasketaan yhteen esimerkiksi kahta metreinä ilmoitettua pituutta, joista toinen on mitattu kahden desimaalin (senttimetrin) tarkkuudella ja toinen kolmen desimaalin (millimetrin) tarkkuudella, joudutaan valitsemaan lähtöarvoista epätarkempi (kaksi desimaalia), jonka mukaisesti vastaus pyöristetään.
Esimerkki: Laske pituuksien 14,39 m ja 3,217 m summa.
\( \mathsf{\text{14,39 m} + \text{3,217 m} = \text{17,607 m} \approx \text{17,61 m}} \)
Pyöristäminen merkitsevien numeroiden perusteella
Esimerkiksi kerto- ja jakolaskujen vastauksia pyöristettäessä tutkitaan lähtöarvojen merkitsevien numeroiden määrää. Tutustutaan ensin merkitseviin numeroihin, jotta niiden avulla pyöristäminen onnistuu.
Merkitsevät numerot
Kokonaislukujen tapauksessa merkitseviä numeroita ovat kaikki numerot, paitsi luvun lopussa olevat nollat.
Esimerkki: Montako merkitsevää numeroa on luvussa
a) 204 912
Luvun lopussa ei ole nollia, joten kaikki numerot ovat merkitseviä.
Vastaus: Luvussa 204 912 on kuusi merkitsevää numeroa.
b) 842 500
Luvun lopussa on kaksi nollaa, joten vain numerot 8, 4, 2 ja 5 ovat merkitseviä.
Vastaus: Luvussa 842 500 on neljä merkitsevää numeroa.
Desimaalilukujen tapauksessa merkitseviä numeroita ovat kaikki numerot, paitsi luvun alussa olevat nollat.
Esimerkki: Montako merkitsevää numeroa on luvussa
a) 3,1415
Luvun alussa ei ole nollia, joten kaikki numerot ovat merkitseviä.
Vastaus: Luvussa 3,1415 on viisi merkitsevää numeroa.
b) 0,00280
Luvun alussa on kolme nollaa, joten vain numerot 2, 8 ja 0 ovat merkitseviä.
Vastaus: Luvussa 0,00280 on kolme merkitsevää numeroa.
Pyöristäminen merkitsevien numeroiden tarkkuuteen
Pyöristystarkkuus voidaan antaa siis myös haluttujen merkitsevien numeroiden perusteella.
Esimerkki: Pyöristä luku 1,893
a) yhden merkitsevän numeron tarkkuuteen
\( \mathsf{\text{1,}{\color{red}|}\text{893} \approx \text{2}} \)
b) kahden merkitsevän numeron tarkkuuteen
\( \mathsf{\text{1,8}{\color{red}|}\text{93} \approx \text{1,9}} \)
c) kolmen merkitsevän numeron tarkkuuteen
\( \mathsf{\text{1,89}{\color{red}|}\text{3} \approx \text{1,89}} \)
Mittaustulosten kerto- ja jakolaskun tapauksessa epätarkkuus saattaisi kertaantua liian suureksi, jos sen vastauksen pyöristämiseen käytettäisiin desimaalien tarkkuutta. Tämän vuoksi tulos pyöristetäänkin merkitsevien numeroiden tarkkuudella.
Esimerkki: Laske A4-paperin pinta-ala, kun sen mitat ovat 29,7 cm ja 21 cm.
\( \mathsf{\text{29,7 cm} \cdot \text{21 cm} = \text{623,7 cm}^2 \approx \text{620 cm}^2} \)
Vastaus: A4-paperin pinta-ala on 620 cm2.
Lähtöarvoista 29,7 oli siis kolmen merkitsevän ja 21 vain kahden merkitsevän numeron tarkkuudella ilmoitettu. Näistä valitaan vastauksen pyöristystarkkuudeksi epätarkempi, eli kaksi merkitsevää numeroa. Jos oltaisiin varmoja, että 21 cm onkin tarkalleen 21,0 cm, niin tällöin vastaus pyöristettäisiin kolmen merkitsevän numeron tarkkuuteen, ja vastaus olisi 624 cm2.
2. Toisen asteen yhtälö
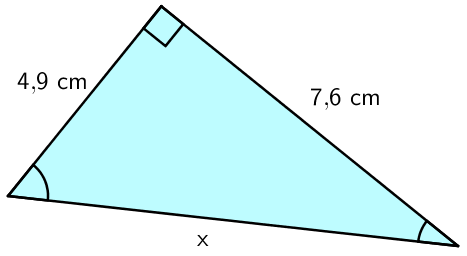
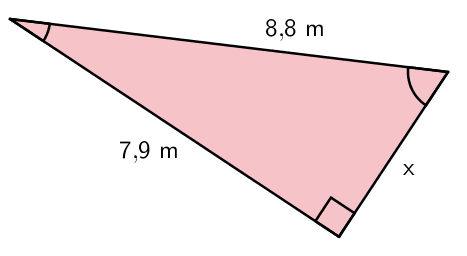
Monet suureiden väliset riippuvuudet eivät rajoitu suoraan tai kääntäen verrannollisuuuteen tai muihin ns. lineaarisiin riippuvuuksiin, jossa suure saadaan kertomalla tai jakamalla toinen suure jollakin luvulla. Suure voi olla riippuvainen toisen suureen neliöstä, jolloin käänteisen ongelman ratkaiseminen vaatii toisen asteen yhtälön ratkaisemista. Tällaisia suureita ovat esimerkiksi neliön sivu ja pinta-ala (\(\mathsf{A = a^2}\)), suorakulmaisen kolmion kateettien pituuksien neliöiden summa ja hypotenuusan neliö (Pythagoraan lause \(\mathsf{a^2 + b^2 = c^2}\)), ympyrän säde ja pinta-ala (\(\mathsf{A \sim r^2}\)) tai fysiikan puolelta ilmanvastus ja nopeus (\(\mathsf{F_v \sim v^2}\)).
Kertausta: Ensimmäisen asteen yhtälö
Aikaisemmin ollaan opittu ratkaisemaan ns. ensimmäisen asteen yhtälöitä, joissa on esiintynyt termejä, joiden aste on ollut 1 tai 0 (vakiotermi). Ensimmäisen asteen yhtälöitä ovat esimerkiksi
\(\mathsf{2x + 1 = 7}\)
\(\mathsf{-3x + 2 = x + 10}\)
Yhtälöitä ratkaistiin vaiheittain lisäämällä, vähentämällä, kertomalla tai jakamalla yhtälöä puolittain tavoitteena saada muuttuja (yleensä x) jäämään yksin yhtälön toiselle puolelle. Puolittain suoritettavaa laskutoimitusta merkittiin yhtälön rivin perään \(||\)-merkkien jälkeen.
Esimerkki: Ratkaise yhtälö.
a) 2x + 1 = 7
\(\begin{align}\mathsf{2x+1} &= \mathsf{7} &&\mathsf{|| -1}\\\mathsf{2x} &= \mathsf{6} &&\mathsf{|| :2}\\\mathsf{x} &= \mathsf{3}\end{align}\)
b) -3x + 2 = x + 10
\(\begin{align}\mathsf{-3x+2} &= \mathsf{x + 10} &&\mathsf{|| -x}\\\mathsf{-4x+2} &= \mathsf{10} &&\mathsf{|| -2}\\\mathsf{-4x} &= \mathsf{8} &&\mathsf{|| :(-4)}\\\mathsf{x} &= \mathsf{-2}\end{align}\)
Toisen asteen yhtälö
Toisen asteen yhtälöllä tarkoitetaan yhtälöä, jossa esiintyy termejä, joiden aste on 2. Toisin sanoen muuttuja (esim. x) on korotettu toiseen potenssiin (neliö). Toisen asteen yhtälöitä ovat esimerkiksi:
\(\mathsf{x^2 = 36}\)
\(\mathsf{5x^2 = 20}\)
\(\mathsf{-2x^2 + 7 = -11}\)
\(\mathsf{x^2 = 4x - 3}\)
Yhtälön ratkaisemisessa käytetään aina käänteisiä laskutoimituksia puolittain, jotta muuttuja saadaan jäämään yksin toiselle puolelle yhtälöä. Toiseen potenssiin korottamiselle eli neliölle vastakkainen laskutoimitus on tietenkin neliöjuuri.
Esimerkki: Ratkaise yhtälö.
a) x2 = 36
\(\begin{align}\mathsf{x^2} &= \mathsf{36} \quad &\mathsf{|| \sqrt{\quad}}\\\mathsf{x} &= \mathsf{6}\\&\textsf{tai}\\\mathsf{x} &= \mathsf{-6}\end{align}\)
b) x2 = 25
\(\begin{align}\mathsf{x^2} &= \mathsf{25} \quad &\mathsf{|| \sqrt{\quad}}\\\mathsf{x} &= \mathsf{\pm5}\end{align}\)
Miksi vastauksia on kaksi, ja miksi b-kohdan vastauksen edessä on \(\pm\)-merkki? Mitä se tarkoittaa?
Jos tarkastellaan esimerkkiä sillä ajatuksella, että "Mikä luku sopii x:n paikalle?" havaitaan, että muuttujan x paikalle sopii sekä positiviinen että negatiivinen ratkaisu. \(\pm\)-merkki on "plusmiinus"-merkki, jolla voidaan ilmoitaa, että molemmat etumerkit (+ tai -) ovat sallittuja. Pidemmin saman voisi merkitä kirjoittamalla ratkaisut erikseen "tai"-sanan avulla.
Laskujärjestys sanoo, että potenssit ja neliöjuuret lasketaan ennen kerto- ja jakolaskuja tai yhteen- ja vähennyslaskuja. Koska yhtälönratkaisussa toimitaan aina käänteisesti myös laskujärjestyksen suhteen, suoritetaan kaikki muut ratkaisun vaiheet ennen neliöjuuren ottamista puolittain.
Esimerkki: Ratkaise yhtälö.
a) 5x2 = 20
\(\begin{align}\mathsf{5x^2} &= \mathsf{20} \quad &&\mathsf{|| :5}\\ \mathsf{x^2} &= \mathsf{4} &&\mathsf{|| \sqrt{\quad}}\\ \mathsf{x} &= \mathsf{\pm2} \end{align}\)
b) -2x2 + 7 = -11
\(\begin{align}\mathsf{-2x^2 + 7} &= \mathsf{-11} \quad &&\mathsf{|| -7}\\ \mathsf{-2x^2} &= \mathsf{-18} \quad &&\mathsf{|| :(-2)}\\ \mathsf{x^2} &= \mathsf{9} &&\mathsf{|| \sqrt{\quad}}\\ \mathsf{x} &= \mathsf{\pm3} \end{align}\)
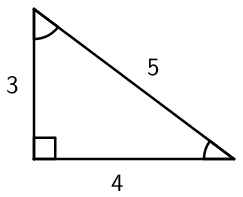
3. Suorakulmainen kolmio
7. luokalla luokteltiin erilaisia kolmioita sen kulmien perusteella. Kolmio voi olla terävä-, suora- tai tylppäkulmainen. Tässä jaksossa (sekä 9. luokan Trigonometria-jaksossa) keskitytään suorakulmaisiin kolmioihin. Suorakulmainen kolmio voidaan ajatella puolikkaana suorakulmiona, jolloin suorakulmaiseen kolmioon liittyvät lainalaisuudet ovat sovellettavissa suorakulmioihin liittyviin käytännön ongelmiin.
Suorakulmaisen kolmion osat
Suoran kulman viereisiä sivuja kutsutaan kateeteiksi ja sitä vastassa olevaa sivua hypotenuusaksi. Hypotenuusa on sivuista pisin.
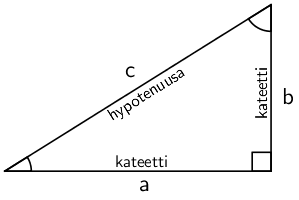
Kateetteja merkitään usein muuttujilla \(\mathsf{a}\) ja \(\mathsf{b}\). Hypotenuusaa merkitään muuttujalla \(\mathsf{c}\).
Suorakulmaisen kolmion pinta-ala
Suorakulmaisen kolmion pinta-ala lasketaan kuten minkä tahansa kolmion pinta-ala, mutta suorakulmaisella kolmiolla kateetit ovat jo lähtökohtaisesti kohtisuorassa toisiaan vastaan, jolloin ne kannattaa valita kannaksi ja korkeudeksi.
\(\mathsf{A = \dfrac{a \cdot b}{2}}\)
Esimerkki: Laske kolmion pinta-ala.
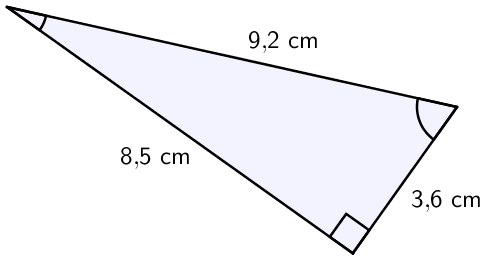
\(\begin{align}\mathsf{A} &= \mathsf{\dfrac{a \cdot b}{2}}\\ &= \mathsf{\dfrac{8,\!5\:cm \cdot3,\!6\:cm}{2}}\\&= \mathsf{\dfrac{30,\!6\:cm^2}{2}}\\&=\mathsf{15,\!3\:cm^2}\\&\approx\mathsf{15\:cm^2}\end{align}\)