MA8 Jakso 4: Potenssit ja polynomit
1. Kertausta
7. luokalla opittiin perusteita kirjainlaskennasta, kun tutustuttiin muuttujiin, muuttujalausekkeisiin sekä niiden sieventämiseen ja arvon laskemiseen. 8. luokalla näitä taitoja kehitetään edelleen tutustumalla yhtälönratkaisuun, polynomeihin sekä potenssilausekkeisiin.
Termi
Termi muodostuu luvun ja muuttujan tulosta. Termiä merkittäessä kertomerkki jätetään merkitsemättä. Lukua kutsutaan termin kertoimeksi ja muuttujaa (sekä myöhemmin sen astetta) muuttujaosaksi.

Erityisesti termin kertoimista pitää muistaa kertoimet 1 ja -1, joiden tapauksessa ykköstä ei merkitä näkyviin, vaan esimerkiksi
\(\mathsf{1a = a}\)
\(\mathsf{-1x=-x}\)
Muuttujalauseke
Muuttujalauseke on lauseke, jossa esiintyy vähintään yksi muuttuja. Esimerkiksi matematiikassa ja fysiikassa esiintyy kaikenlaisia muuttujalausekkeita, joiden avulla mallinnetaan esimerkiksi luonnon ilmiöitä, kappaileiden kokoa, muotoa tai prosenttilaskennan laskusääntöjä.
Muuttujalausekkeen arvon laskeminen
Muuttujalausekkeen arvon laskeminen on yksi peruskoulumatematiikan tärkeimmistä opittavista taidoista. Muuttujalausekkeen arvo voidaan laskea, jos tunnetaan muuttujan arvo. Muuttujan arvo sijoitetaan lausekkeeseen muuttujan paikalle, jonka jälkeen lausekkeen arvo voidaan laskea.
Esimerkki: Laske lausekkeen \(\mathsf{3x + 4}\) arvo, kun muuttuja saa arvon \(\mathsf{x = 2}\).
\(\begin{align}\phantom{=}&\mathsf{3x + 4}\\ =\;&\mathsf{3\cdot 2 + 4}\\ =\;&\mathsf{6 + 4}\\ =\;&\mathsf{10}\end{align}\)
Sijoitettaessa negatiivista lukua muuttujan paikalle, tulee luku kirjoittaa sulkeiden sisään.
Esimerkki: Laske lausekkeen \(\mathsf{3x + 4}\) arvo, kun muuttuja saa arvon \(\mathsf{x = -1}\).
\(\begin{align}\phantom{=}&\mathsf{3x + 4}\\ =\;&\mathsf{3\cdot (-1) + 4}\\ =\;&\mathsf{-3 + 4}\\ =\;&\mathsf{1}\end{align}\)
Lausekkeen sieventäminen
Peräkkäisistä termeistä koostuvaa muuttujalauseketta kutsutaan polynomiksi. Tämä käsite tarkentuu myöhemmässä jaksossa 8. luokalla. 7. luokalla opittiin sieventämään muuttujalausekkeessa olevia samanmuotoisia termejä (yhteen- ja vähennyslasku). Samanmuotoisilla termeillä on täsmälleen sama muuttujaosa.
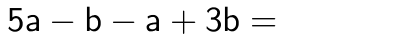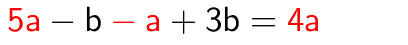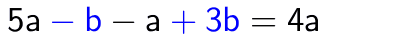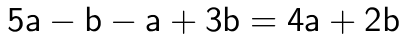
Lisäksi opittiin sieventämään lausekkeita, joissa termiin kohdistuu kerto- tai jakolasku.
a) \(\mathsf{5 \cdot 6x = 30x}\)
b) \(\mathsf{\dfrac{28a}{-7} = -4a}\)
Lausekkeen kertominen luvulla
Kertolaskun yhteydessä 7. luokalla opittiin ns. osittelulakiin perustuva päässälaskumenetelmä, jonka avulla voitiin laskea helposti kertolasku, jonka toisena tekijänä on suuri luku. Suuri luku pilkotaan osiin (ykkösiin, kymmeniin, satoihin, ...), kerrotaan osia, ja yhdistetään uudet osat takaisin yhdeksi luvuksi. Esimerkiksi
\(\begin{array}{l}\mathsf{\quad 9 \cdot 183}\\ \mathsf{=9 \cdot (100 + 80 + 3)}\\ \mathsf{=900 + 720 + 27}\\ \mathsf{=1647}\end{array}\)
Tätä menetelmää käytetään myös tilanteessa, jossa muuttujalauseketta kerrotaan luvulla (tai termillä).
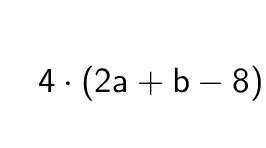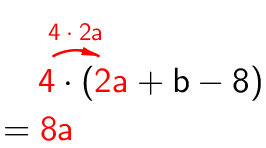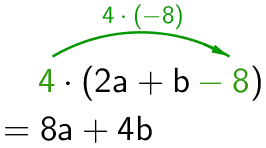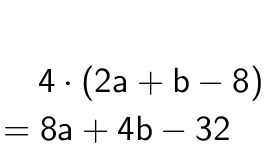
Kertolasku kohdistuu siis kaikkiin muuttujalausekkeen termeihin.
2. Potenssi ja neliöjuuri
Potenssi
Potenssimerkinnän avulla voidaan lyhentää kertolaskua, missä sama luku esiintyy tulon tekijänä useamman kerran. Potenssimerkinnässä tulon tekijän oikeaan yläkulmaan kirjoitetaan luku, joka kertoo kuinka monta kertaa tekijä kertolaskussa esiintyy. Esimerkiksi
\(\mathsf{2 \cdot 2 \cdot 2 \cdot 2 = 2^4}\)
Tulon tekijää (2) kutsutaan kantaluvuksi, ja yläkulmassa olevaa lukua (4) kutsutaan eksponentiksi. Kyseinen merkintä sanottaisiin "Kaksi potenssiin neljä", "Kaksi neljänteen" tai "Kaksi korotettuna neljänteen potenssiin".
Potenssin arvoa laskettaessa potenssimerkintä voidaan kirjoittaa ensin kertolaskuna, ja laskea kertolasku normaalisti tämän jälkeen.
Esimerkki: Laske.
a) \(\mathsf{6^2 = 6 \cdot 6 = 36}\)
b) \(\mathsf{7^2= 7 \cdot 7 = 49}\)
c) \(\mathsf{(-5)^2 = -5 \cdot (-5) = 25}\)
d) \(\mathsf{3^4 = 3 \cdot 3 \cdot 3 \cdot 3 = 81}\)
Kuten yllä olevasta esimerkistä huomataan, niin kantaluku voi olla myös negatiivinen. Negatiivinen kantaluku tulee kirjoittaa sulkeiden sisään. Jos sulkeita ei merkitä, potenssi ei vaikuta miinusmerkkiin, vaan miinusmerkki pysyy potenssin arvon edessä.
Esimerkki: Laske.
a) \(\mathsf{(-4)^2 = -4 \cdot (-4) = 16}\)
b) \(\mathsf{-4^2 = -4 \cdot 4 = -16}\)
Neliöjuuri
Kuten peruslaskutoimituksilla aikaisemmin havaittiin, myös potensseilla on olemassa käänteiset laskutoimitukset. Yleisesti niitä voisi kutsua juuri-laskuiksi, mutta keskitytään nyt toiseen potenssiin korottamisen käänteiseen laskutoimitukseen eli neliöjuureen.
\(\mathsf{5^2 = 25 \qquad \Rightarrow \qquad \sqrt{25} = 5}\)
Neliöjuuren merkintänä käytetään erityistä juuri-merkkiä \(\sqrt{\rule{1em}{0pt}\rule{0pt}{1em}}\). Merkin alla olevaa lukua kutsutaan juurrettavaksi. Neliöjuuri vastaa siis kysymykseen "Mikä luku on kerrottu itsellään, että saadaan vastaukseksi juurrettava?".
Yleisesti luvun \(\mathsf{x}\) neliöjuuri \(\mathsf{\sqrt{x} = a}\) on siis ei-negatiivinen luku, joka itsellään kerrottuna on luku \(\mathsf{x}\).
\(\mathsf{x = a \cdot a = a^2 \quad \Leftrightarrow \quad \sqrt{x} = a \quad}\) kun \(\mathsf{a \geq 0}\)
Esimerkki: Laske.
a) \(\mathsf{\sqrt{16} = 4}\)
b) \(\mathsf{\sqrt{36} = 6}\)
c) \(\mathsf{\sqrt{100} = 10}\)
d) \(\mathsf{\sqrt{1} = 1}\)
Laskujärjestys
Uusien laskutoimitusten myötä päivitetään myös listaa laskujärjestyksestä. Koska potenssi on lyhyempi merkintä voidaan kasvattaa sulkeiden avulla. Neliöjuuren sisään voidaan myös kirjoittaa laskutoimituksia, jolloin neliöjuurimerkkiä venytetään kattamaan kaikki juurrettavaan kuuluvat osat.
- Sulkeet
- Potenssi ja neliöjuuri
- Kerto- ja jakolasku
- Yhteen- ja vähennyslasku
Esimerkki: Laske.
a) \(\mathsf{(12-8)^2 = 4^2 = 16}\)
b) \(\mathsf{6^2 - 11 = 36 - 11 = 35}\)
c) \(\mathsf{5 \cdot 2^3 = 5 \cdot 8 = 40}\)
d) \(\mathsf{\dfrac{4^2}{2^4} = \dfrac{16}{16} = 1}\)
e) \(\mathsf{\sqrt{8+17} = \sqrt{25} = 5}\)
f) \(\mathsf{\sqrt{3^2} = \sqrt{9} = 3}\)
3. Potenssin laskusääntöjä
Potenssilaskuihin liittyy useita erilaisia laskusääntöjä, joiden tarkoitus on helpottaa ja nopeuttaa potenssien laskemista. Sieventämällä lausekkeita etukäteen varsinainen laskutoimitus muuttuu yleensä helpommaksi. Lisäksi seuraavia laskusääntöjä tarvitaan tulevien sääntöjen pohjana.
Tulon ja osamäärän korottaminen potenssiin
\(\mathsf{(ab)^n = a^n b^n}\)
\(\mathsf{\left(\dfrac{a}{b}\right)^n = \dfrac{a^n}{b^n}}\)
Samankantaisten potenssien tulo ja osamäärä
\(\mathsf{a^m \cdot a^n = a^{m+n}}\)
\(\mathsf{\dfrac{a^m}{a^n} = a^{m-n}}\)
Eksponenttina negatiivinen luku tai nolla
\(\mathsf{a^{-n} = \dfrac{1}{a^n}}\)
\(\mathsf{a^{0} = 1}\)
Lisätietoa: Potenssin potenssi
\(\mathsf{(a^n)^m = a^{n \cdot m}}\)
Tulon ja osamäärän potenssi
Johdatellaan aiheeseen esimerkin avulla, jossa sulkulauseke on korotettu potenssiin. Koska potenssi on vain lyhyempi tapa merkitä kertolaskua, voidaan se aina pilkkoa kertolaskuksi, järjestellä tekijät uudelleen ja kasata toiseen muotoon.
\(\begin{align}(\mathsf{3 \cdot 4)^2} &= \mathsf{(3 \cdot 4) \cdot (3 \cdot 4)}\\ &= \mathsf{3 \cdot 4 \cdot 3 \cdot 4}\\ &= \mathsf{3 \cdot 3 \cdot 4 \cdot 4}\\ &= \mathsf{3^2 \cdot 4^2}\end{align}\)
Jos potenssimerkinnän kantalukuna on siis tulo, niin sulkeet voidaan poistaa korottamalla kaikki tulon tekijät kyseiseen potenssiin.
\(\mathsf{(ab)^n = a^n b^n}\)
Esimerkki: Sievennä.
a) \(\mathsf{(5x)^2 = 25x^2}\)
b) \(\mathsf{(-2a)^3 = -8a^3}\)
c) \(\mathsf{(4ab)^2 = 16a^2b^2}\)
Vastaava laskusääntö on käytössä myös, kun korotetaan osamäärä potenssin.
\(\mathsf{\left(\dfrac{a}{b}\right)^n = \dfrac{a^n}{b^n}}\)
Esimerkki: Sievennä.
a) \(\mathsf{\left(\dfrac{3}{4}\right)^2 = \dfrac{9}{16}}\)
b) \(\mathsf{\left(\dfrac{a}{5}\right)^2 = \dfrac{a^2}{25}}\)
c) \(\mathsf{\left(\dfrac{-2x}{y}\right)^2 = \dfrac{4x^2}{y^2}}\)
Samankantaisten potenssien tulo ja osamäärä
Johdatellaan aiheeseen taas esimerkin avulla, missä kahden samakantaisen potenssin tulo voidaan yhdistää yhdeksi potenssimerkinnäksi.
\(\begin{align}\mathsf{{\color{red}3^2} \cdot {\color{blue}3^3}} &= \mathsf{{\color{red}3\cdot 3} \cdot {\color{blue}3 \cdot 3 \cdot 3}}\\ &= \mathsf{3^5}\end{align}\)
Samankantaisten potenssien tulossa eksponentit voidaan siis laskea yhteen.
\(\mathsf{a^m \cdot a^n = a^{m+n}}\)
Esimerkki: Sievennä.
a) \(\mathsf{2^4 \cdot 2^2 = 2^6}\)
b) \(\mathsf{(-1)^6 \cdot (-1)^7 = (-1)^{13}}\)
c) \(\mathsf{a \cdot a^2 \cdot a^3 = a^6}\)
Samankantaisten potenssien osamäärässä voidaan supistaa jaettavasta ja jakajasta yhtä monta samaa tekijää.
\(\require{enclose}\begin{align}\mathsf{\dfrac{5^6}{5^4}} &= \mathsf{\dfrac{5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5}{5 \cdot 5 \cdot 5 \cdot 5}}\\ &= \mathsf{\dfrac{\enclose{horizontalstrike}{5 \cdot 5 \cdot 5 \cdot 5} \cdot 5 \cdot 5}{\enclose{horizontalstrike}{5 \cdot 5 \cdot 5 \cdot 5}}}\\ &= \mathsf{5^2}\end{align}\)
Vastaavasti samankantaisten potenssien jakolaskussa eksponentit vähennetään toisistaan.
\(\mathsf{\dfrac{a^m}{a^n} = a^{m-n}}\)
Esimerkki: Sievennä.
a) \(\mathsf{\dfrac{5^7}{5^5} = 5^2 = 25}\)
b) \(\mathsf{\dfrac{p^{11}}{p^7} = p^4}\)
c) \(\mathsf{\dfrac{(-3)^5}{-3} = (-3)^4}\)
Eksponenttina negatiivinen luku tai nolla
Eksponentti voi olla myös negatiivinen. Lähdetään tutkimaan asiaa ratkaisemalla esimerkki samankantaisten potenssien osamäärästä. Sievennetään esimerkki kahdella eri tavalla.
Esimerkki: Sievennä.
Tapa 1:
\(\mathsf{\dfrac{2^3}{2^5} = a^{3-5} = 2^{-2}}\)
Tapa 2:
\(\require{enclose}\mathsf{\dfrac{2^3}{2^5} = \dfrac{\enclose{horizontalstrike}{2 \cdot 2 \cdot 2}}{\enclose{horizontalstrike}{2 \cdot 2 \cdot 2}\!\cdot 2 \cdot 2} = \dfrac{1}{2 \cdot 2} = \dfrac{1}{2^2}}\)
Esimerkistä huomataan, että negattivinen eksponentti tarkoittaa vastaavan positiivisen eksponentin potenssimerkintää käänteislukuna. Tästä saadaan sievennyssääntö negatiivisen eksponentin tapaukseen.
\(\mathsf{a^{-n} = \dfrac{1}{a^n}}\)
Esimerkki: Sievennä.
a) \(\mathsf{5^{-2} = \dfrac{1}{5^2} = \dfrac{1}{25} = 0,\!04}\)
b) \(\mathsf{3^{-1} = \dfrac{1}{3^1} = \dfrac{1}{3}}\)
c) \(\mathsf{10^{-4} = \dfrac{1}{10^4} = \dfrac{1}{10\:000} = 0,\!0001}\)
Eksponenttina nolla
Samalla tavalla voidaan tarkastella tilannetta, jossa eksponenttina on nolla. Sievennetään samankantaisten potenssien osamäärä jälleen kahdella eri tavalla.
Esimerkki: Sievennä.
Tapa 1: \(\qquad\mathsf{\dfrac{4^3}{4^3} = 4^{3-3} = 4^0}\)
Tapa 2: \(\qquad\require{enclose}\mathsf{\dfrac{4^3}{4^3} = \dfrac{\enclose{horizontalstrike}{4 \cdot 4 \cdot 4}}{\enclose{horizontalstrike}{4 \cdot 4 \cdot 4}} = \dfrac{64}{64} = 1}\)
Johtopäätös: \(\mathsf{4^0 = 1}\)
Lukujen 4 ja 3 paikalle voidaan kirjoittaa (lähes) mitkä tahansa luvut, ja vastaukseksi saadaan aina yksi. Näin ollen voidaan todeta, että luvun nollas potenssi on aina yksi.
\(\mathsf{a^0 = 1}\)
Lisätietoa: Potenssin potenssi
Potenssin korottaminen potenssiin merkitään kirjoittamalla aikasempi potenssi sulkeisiin ja kirjoittamalla jälkimmäisen potenssin eksponentti sulkeiden ulkopuolle. Sulkeilla on merkitystä laskujärjetsyksen kannalta. Tarkastellaan esimerkkiä, jonka avulla on helpompi hahmottaa tilannetta.
Esimerkki: Kirjoita yhtenä potenssina.
\(\mathsf{(a^2)^3 = a^2 \cdot a^2 \cdot a^2 = a^6}\)
Aluksi sulkeiden sisällä ollut \(\mathsf{a^2}\) toimii siis kantalukuna, jota kerrotaan itsellään kolmesti, kuten ulompi eksponentti osoittaa. Tämän jälkeen käytetään samankantaisten potenssien tulon laskusääntöä, jolloin \(\mathsf{a^2 \cdot a^2 \cdot a^2 = a^{2+2+2} = a^6}\). Vastaava tulos saadaan kun eksponentit kerrotaan keskenään. \(\mathsf{a^{2+2+2} = a^{2\cdot 3} = a^6}\). Yleisesti potenssin potenssin laskukaava on muotoa
\(\mathsf{(a^m)^n = a^{m\cdot n}}\)
Jos sulkeita ei ole, esimerkin merkintä näyttäisi seuraavalta:
\(\mathsf{a^{2^3}}\),
jolloin laskujärjestyksen mukaisesti laskettaisiin ensin eksponenttien muodostama potenssimerkintä \(\mathsf{2^3}\). Tästä saataisiin siis
\(\mathsf{a^{2^3} = a^8}\)
Sulkeilla on siis suuri merkitys myös tässä tilanteesa. Jos esimerkiksi laskentaohjelma ei muotoile syötettä on sulkeiden kanssa oltava tarkkana.
\(\texttt{3^3^3 = 7 625 597 484 987}\)
\(\texttt{(3^3)^3 = 19 683}\)
4. Kymmenpotenssi
Todella suuret ja pienet luvut ilmoitetaan usein vaivan ja tilan säästämiseksi sekä vertailun helpottamiseksi kymmenpotenssin avulla. Kymmenpotenssimuoto on tulo, joka koostuu kertoimesta sekä kymmenen potenssista.
\(\mathsf{3\:140\:000 = 3,\!14 \cdot 10^6}\)
Kertoimen tulee olla vähintään yksi, mutta sen tulee olla pienempi kuin kymmenen. Yleisesti ottaen kymmenpotenssimuoto voidaan määritellä seuraavasti:
\(\mathsf{a \cdot 10^n, \rule{4em}{0pt} \text{missä } 1 \leq a < 10}\)
Kymmenpotenssimuodossa luvun 10 eksponentti kertoo pilkunsiirtojen lukumäärän. Positiivinen eksponentti tuottaa suuria lukuja, ja negatiinen eksponentti tuottaa pieniä lukuja.
Esimerkki: Kirjoita luku ilman kymmenpotenssimuotoa.
a) \(\mathsf{5 \cdot 10^3 = 5 \cdot 1000 = 5\:000}\)
b) \(\mathsf{5,\!4 \cdot 10^3 = 5,\!4 \cdot 1000 = 5\:400}\)
c) \(\mathsf{5 \cdot 10^{-3} = 5 \cdot 0,\!001 = 0,\!005}\)
d) \(\mathsf{5,\!4 \cdot 10^{-3} = 5,\!4 \cdot 0,\!001 = 0,\!0054}\)
Esimerkki: Kirjoita luku kymmenpotenssimuodossa.
a) \(\mathsf{4\:000\:000 = 4 \cdot 10^6}\)
b) \(\mathsf{120\:000 = 1,\!2 \cdot 10^5}\)
c) \(\mathsf{0,\!00007 = 7 \cdot 10^{-5}}\)
d) \(\mathsf{0,\!0593 = 5,\!93 \cdot 10^{-2}}\)
5. Polynomi
Polynomi-sana tulee kreikan kielestä, ja tarkoittaa moniosaista. Osalla tarkoitetaan tässä yhteydessä termejä, eli polynomi on monista termeistä koostuva muuttujalauseke. Laajennetaan termin käsitettä 7. luokasta ottamalla mukaan aiemmin tässä jaksossa opitut potenssit.
Termi
Termi on kertoimen ja muuttujaosan tulo. Kerroin on luku, ja muuttujaosassa on nimensä mukaisesti muuttuja. Muuttuja voi olla korotettuna potenssiin, jolloin sen eksponenttia kutsutaan termin asteeksi.
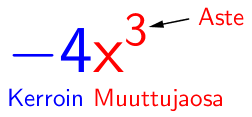
Termejä luokitellaan niiden asteen mukaan, eli esimerkiksi \(\mathsf{6x^3}\) on kolmannen asteen termi, \(\mathsf{-7x^5}\) on viidennen asteen termi jne.
Huomaathan erityisesti seuraavien termien asteet:
- Termin \(\mathsf{5x}\) aste on 1, sillä \(\mathsf{5x = 5x^1}\).
- Vakiotermin \(\mathsf{-2}\) aste on 0, sillä \(\mathsf{-2 = -2x^0}\).
Termit ovat samanmuotoisia, jos niillä on täsmälleen sama muuttujaosa, eli siis sama muuttuja sekä aste. Vain samanmuotoisia termejä voidaan laskea yhteen ja vähentää toisistaan.
Esimerkki: Sievennä.
a) \(\mathsf{2x^2 + 3x^2 = 5x^2}\)
b) \(\mathsf{4x^3 - 5x^3 = -x^3}\)
c) \(\mathsf{6x^2 + 4x^2 + 3x - x = 10x^2 + 2x}\)
d) \(\begin{align}&\mathsf{{\color{red}5x^3}\;{\color{blue}-\;2x^2} + 6 \;{\color{red}-\;x^3}\;{\color{blue}+\;3x^2} -7}\\ =\;&\mathsf{{\color{red}4x^3} \;{\color{blue}+\;x^2} - 1}\end{align}\)
Termien kerto- ja jakolaskussa kertoimet kerrotaan (jaetaan) erikseen ja muuttujaosat erikseen.
Esimerkki: Sievennä.
a) \(\mathsf{{\color{red}2}{\color{blue}x^2} \cdot {\color{red}3}{\color{blue}x^3} = {\color{red}6}{\color{blue}x^5}}\)
b) \(\mathsf{{\color{red}-}{\color{blue}x} \cdot {\color{red}4}{\color{blue}x^2} = {\color{red}-4}{\color{blue}x^3}}\)
c) \(\mathsf{\dfrac{{\color{red}12}{\color{blue}x^3}}{{\color{red}4}{\color{blue}x^2}} = {\color{red}3}{\color{blue}x}}\)
d) \(\mathsf{\dfrac{{\color{red}-42}{\color{blue}x^7}}{{\color{red}7}{\color{blue}x^3}} = {\color{red}-6}{\color{blue}x^4}}\)
Polynomi
Polynomi koostuu yhdestä tai useammasta termistä. Yhden termin polynomeja kutsutaan erityisesti monomeiksi, kahden termin polynomeja binomeiksi ja kolmen termin polynomeja trinomeiksi. Näistä termeistä on hyötyä myöhemmissä opinnoissa, kun käsitellään esimerkiksi binomin neliötä.
\(\mathsf{4x^3 + x^2 - 5x + 9}\)
Polynomissa termit järjestellään aina termien asteluvun mukaiseen suuruusjärjestykseen suuriasteisimmasta termistä pienempään. Polynomin aste on sen korkea-asteisimman termin aste.
Polynomin arvo
Polynomin arvo lasketaan sijoittamalla annettu muuttujan arvo lausekkeeseen.
Esimerkki: Laske polynomin \(\mathsf{5x^3 + 2x}\) arvo, kun
a) \(\mathsf{{\color{red}x} = {\color{red}2}}\)
\(\begin{align}\mathsf{5{\color{red}x}^3 + 4{\color{red}x}} &= \mathsf{5 \cdot {\color{red}2}^3 + 4 \cdot {\color{red}2}}\\ &= \mathsf{5 \cdot 8 + 4 \cdot 2}\\ &= \mathsf{40 + 8}\\ &= \mathsf{48}\end{align}\)
b) \(\mathsf{{\color{blue}x} = -{\color{blue}2}}\)
\(\begin{align}\mathsf{5{\color{blue}x}^3 + 4{\color{blue}x}} &= \mathsf{5 \cdot {\color{blue}(-2)}^3 + 4 \cdot {\color{blue}(-2)}}\\ &= \mathsf{5 \cdot (-8) + 4 \cdot (-2)}\\ &= \mathsf{-40 - 8}\\ &= \mathsf{-48}\end{align}\)
6. Polynomien laskusääntöjä
Aiemmin on tutustuttu peruslaskutoimituksiin yksittäisten termien (monomien) tapauksessa. Tässä luvussa laajennetaan peruslaskutoimitukset koskemaan kokonaisia polynomeja.
Polynomien yhteen- ja vähennyslasku
Ennen varsinaista polynomien yhteen- tai vähennyslaskua tutustutaan tilanteeseen, jossa sulkeiden sisässä olevan polynomin edessä on jokin etumerkki (+ tai -). Tämän jälkeen meidän on helpompi sieventää sulkeita pois myös yhteen- ja vähennyslaskun tapauksessa.
Esimerkki: Sievennä.
a) \(\mathsf{+(2x-4) = 2x - 4}\)
b) \(\mathsf{-(2x-4) = -2x + 4}\)
c) \(\mathsf{+(-4x^2 + 5x - 7) = -4x^2 + 5x - 7}\)
d) \(\mathsf{-(-4x^2 + 5x - 7) = 4x^2 - 5x + 7}\)
Plusmerkki (+) sulkeiden edessä ei siis vaikuta sulkeiden poistossa termeihin. Miinusmerkki (-) sulkeiden edessä vaihtaa kaikkien polynomin termien etumerkin. Näiden avulla voidaan sieventää myös varsinaiset polynomien yhteen- ja vähennyslaskut. Ensin poistetaan sulkeet polynomien ympäriltä, ja tämän jälkeen sievennetään samanmuotoiset termit.
Esimerkki: Sievennä.
a)
\(\begin{align}&\mathsf{({\color{red}5x - 3}) + ({\color{blue}2x + 6})}\\ =\;&\mathsf{{\color{red}5x - 3}\;{\color{blue}+\;2x + 6}}\\ =\;&\mathsf{7x + 3}\end{align}\)
b)
\(\begin{align}&\mathsf{{\color{red}-x+6} - ({\color{blue}3x-4})}\\ =\;&\mathsf{{\color{red}-x +6}\;{\color{blue}-\;3x +4}}\\ =\;&\mathsf{-4x +2}\end{align}\)
c)
\(\begin{align}&\mathsf{({\color{red}2x^2+8}) + ({\color{blue}-3x^2-3})}\\ =\;&\mathsf{{\color{red}2x^2+8}\;{\color{blue}-\;3x^2-3}}\\ =\;&\mathsf{-x^2 + 5}\end{align}\)
d)
\(\begin{align}&\mathsf{{\color{red}-7x^2 + x} - ({\color{blue}-2x^2 + x})}\\ =\;&\mathsf{{\color{red}-7x^2 + x}\;{\color{blue}+\;2x^2 - x}}\\ =\;&\mathsf{-5x^2}\end{align}\)
Polynomien kertolasku
Tarkastellaan ensin polynomin ja monomin (termin) kertolaskua, joka on osittain kertausta luvun ja muuttujalausekkeen tulosta. Monomilla kerrotaan kaikki polynomin termit erikseen.
Esimerkki: Sievennä.
a) \(\mathsf{4 \cdot (2x-4) = 8x - 16}\)
b) \(\mathsf{4x \cdot (2x-4) = 8x^2 - 16x}\)
c) \(\mathsf{-3x^2 \cdot (-7x^3 + x) = 21x^5 -3x^3}\)
d) \(\mathsf{(6x^2 - 3x - 7) \cdot 5x = 30x^3 - 15x^2 - 35x}\)
Kahden polynomin kertolaskussa kaikilla ensimmäisen polynomin termeillä kerrotaan vuorollaan kaikki toisen polynomin termit.
Esimerkki: Laske.
Lisätietoa: Binomin neliö
Binomin neliö ei sinällään ole haastava sievennettävä, mutta laskukaavan käyttö nopeuttaa sievennystä, jos binomin neliöitä on useita. Varsinkin tilanteen tunnistaminen toisin päin muodostuu myöhemmissä opinnoissa hyödylliseksi taidoksi esimerkiksi funktioiden nollakohtia etsittäessä.
Johdetaan binomin neliön laskukaava tuttujen laskusääntöjen avulla. Vaiheittainen johdanto löytyy kultapaketin tehtävästä Binomin neliö.
\(\begin{align}\mathsf{(a + b)^2} &= \mathsf{(a+b) \cdot (a+b)}\\ &=\mathsf{a^2 + ab + ab + b^2}\\ &=\mathsf{a^2 + 2ab + b^2}\end{align}\)
Laskukaavaa voidaan nyt käyttää kaikenlaisten binomien neliöiden sieventämiseen sijoittamalla muuttujien \(\mathsf{a}\) ja \(\mathsf{b}\) paikalle binomin termit.
Esimerkki: Sievennä.
a) \(\mathsf{(x+1)^2 = x^2 + 2x + 1}\)
b) \(\mathsf{(x+6)^2 = x^2 + 12x + 36}\)
c) \(\mathsf{(8x+5)^2 = 64x^2 + 80x + 25}\)
Binomille \(\mathsf{a-b}\) on myös johdettu oma laskukaavansa, mutta ottamalla etumerkit huomioon aiemmassa laskukaavassa ei toinen laskukaava ole välttämätön muistaa. Ainoastaan 1. asteen termin etumerkki vaihtuu.
\(\begin{align}\mathsf{(a - b)^2} &= \mathsf{(a-b) \cdot (a-b)}\\ &=\mathsf{a^2 - ab - ab + b^2}\\ &=\mathsf{a^2 - 2ab + b^2}\end{align}\)
Esimerkki: Sievennä.
a) \(\mathsf{(x-1)^2 = x^2 - 2x + 1}\)
b) \(\mathsf{(x-6)^2 = x^2 - 12x + 36}\)
c) \(\mathsf{(8x-5)^2 = 64x^2 - 80x + 25}\)
7. Lisätietoa: Toisen asteen yhtälö
Aikaisemmin ollaan opittu ratkaisemaan ns. ensimmäisen asteen yhtälöitä, joissa on esiintynyt termejä, joiden aste on ollut 1 tai 0 (vakiotermi). Toisen asteen yhtälöllä tarkoitetaan yhtälöä, jossa esiintyy termejä, joiden aste on 2. Toisin sanoen muuttuja (esim. x) on korotettu toiseen potenssiin (neliö). Toisen asteen yhtälöitä ovat esimerkiksi
a) \(\mathsf{x^2 = 36}\)
b) \(\mathsf{5x^2 = 20}\)
c) \(\mathsf{-2x^2 + 7 = -11}\)
d) \(\mathsf{x^2 = 4x - 3}\)
Yhtälön ratkaisemisessa käytetään aina käänteisiä laskutoimituksia puolittain, jotta muuttuja saadaan jäämään yksin toiselle puolelle yhtälöä. Toiseen potenssiin korottamiselle eli neliölle vastakkainen laskutoimitus on tietenkin neliöjuuri.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{x^2} &= \mathsf{36} \quad &\mathsf{|| \sqrt{\quad}}\\\mathsf{x} &= \mathsf{\pm6}\end{align}\)
Miksi vastauksen edessä on \(\pm\)-merkki? Mitä se tarkoittaa?
Jos tarkastellaan esimerkkiä sillä ajatuksella, että "Mikä luku sopii x:n paikalle?" havaitaan, että muuttujan x paikalle sopii sekä positiviinen \(\mathsf{6}\) että negatiivinen \(\mathsf{-6}\). \(\pm\)-merkki on "plusmiinus"-merkki, jolla voidaan ilmoitaa, että molemmat etumerkit (+ tai -) ovat sallittuja. Pidemmin saman voisi merkitä kirjoittamalla ratkaisut erikseen "tai"-sanan avulla.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{x^2} &= \mathsf{36} \quad &\mathsf{|| \sqrt{\quad}}\\\mathsf{x} &= \mathsf{6}\\&\textsf{tai}\\\mathsf{x} &= \mathsf{-6}\end{align}\)
Laskujärjestys sanoo, että potenssit ja neliöjuuret lasketaan ennen kerto- ja jakolaskuja tai yhteen- ja vähennyslaskuja. Koska yhtälönratkaisussa toimitaan aina käänteisesti myös laskujärjestyksen suhteen, suoritetaan kaikki muut ratkaisun vaiheet ennen neliöjuuren ottamista puolittain.
Esimerkki: Ratkaise yhtälö.
a)
\(\begin{align}\mathsf{5x^2} &= \mathsf{20} \quad &&\mathsf{|| :5}\\ \mathsf{x^2} &= \mathsf{4} &&\mathsf{|| \sqrt{\quad}}\\ \mathsf{x} &= \mathsf{\pm2} \end{align}\)
b)
\(\begin{align}\mathsf{-2x^2 + 7} &= \mathsf{-11} \quad &&\mathsf{|| -7}\\ \mathsf{-2x^2} &= \mathsf{-18} \quad &&\mathsf{|| :(-2)}\\ \mathsf{x^2} &= \mathsf{9} &&\mathsf{|| \sqrt{\quad}}\\ \mathsf{x} &= \mathsf{\pm3} \end{align}\)
8. Lisätietoa: Binääriluvut
Tietokoneiden ja muiden elektronisten laitteiden muisti koostuu biteistä. Bittiä kuvataan usein numeroilla 1 ja 0. Erilaiset muistityypit tallentavat bitit hieman eri menetelmin:
- Mekaaniset muistit (reikäkortit ja -nauhat)
- Magneettiset muistit (kiintolevyt, C- ja VHS-kasetit, levykkeet)
- Optiset levyt (CD, DVD, Blue-ray)
- Puolijohdemuistit - "Flash"-muistit (SSD-levyt, muistitikut ja -kortit)
Yhteistä kaikilla menetelmillä on kuitenkin se, että tieto on tallennettu biteiksi. Muistin määrää kuvataan usein tavuina, joka koostuu kahdeksasta bitistä. Peräkkäin kirjoitettuja bittejä voidaan kuvata lukuina, jolloin muodostuu binäärilukuja.
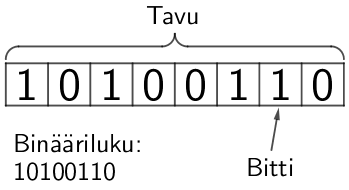
Johdatus kantalukujärjestelmiin
Tutustutaan kantalukujärjestelmään tutun kymmenjärjestelmän (desimaalijärjestelmän) avulla. Aiemmin on opittu, että luvussa jokaisella numerolla on oma paikkansa. Jokainen paikka kuvaa jotakin suuruusluokkaa (ykköset, kymmenet, sadat, tuhannet, ...). Näin ollen luku voidaan pilkkoa summaksi käyttäen kyseisiä suuruusluokkia.
\(\mathsf{2845 = 2000 + 800 + 40 + 5}\)
Muutetaan summattavat kymmenpotenssimerkinnäksi, jolloin nähdään kunkin numeron paikalla on oma eksponenttinsa.
\(\begin{align}\mathsf{2845} &= \mathsf{2000 + 800 + 40 + 5}\\&= \mathsf{2 \cdot 10^3 + 8 \cdot 10^2 + 4 \cdot 10^1 + 5 \cdot 10^0}\end{align}\)
Kun käytössä on kymmenen erilaista numeromerkkiä (0 - 9) voidaan luku pilkkoa potenssien summaksi, jossa kantalukuna on 10 ja kukin potenssi merkitsee yhden numeron paikkaa luvussa. Kyseistä lukujärjestelmää kutsutaan siis kymmenkantaiseksi järjestelmäksi.
Binääriluvut (kaksikantaiset luvut)
Binääriluvut ovat vastaavasti kaksikantaisia lukuja, eli ne voidaan ilmoittaa kymmenjärjestelmässä potenssien summana, missä kantalukuna on 2. Jotta erikantaiset luvut erotetaan toisistaan, merkitään käytetty kanta alaindeksinä luvun perään.
Esimerkki: Muuta kymmenkantaiseksi.
a)
\(\begin{align}\mathsf{1001_2} &= \mathsf{1 \cdot 2^3 + 0 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0}\\&= \mathsf{1 \cdot 8 + 0 \cdot 4 + 0 \cdot 2 + 1 \cdot 1}\\&= \mathsf{8 + 0 + 0 + 1}\\&=\mathsf{9_{10}}\end{align}\)
b)
\(\begin{align}\mathsf{10100110_2} &= \mathsf{1 \cdot 2^7 + 1 \cdot 2^5 + 1 \cdot 2^2 + 1 \cdot 2^1}\\&= \mathsf{128 + 32 + 4 + 2}\\&= \mathsf{168_{10}}\end{align}\)
Kymmenkantaisten lukujen muuntamiseksi binääriluvuiksi on olemassa erilaisia vaiheittaisia toimintaohjeita (algoritmeja), nettimuuntimia sekä ohjelmointikielten funktioita, mutta pienten lukujen muunnokset menevät hyvästä päässälaskusta. Tarkoituksena on siis pilkkoa luku summaksi, jossa käytetään vain kahden potensseja 1, 2, 4, 8, 16, 32, 64, 128, 256, jne. Näitä vastaavien potenssimerkintöjen eksponentit kertovat ykkösten ja nollien paikat binääriluvussa.
Esimerkki: Muuta binääriluvuksi.
a) \(\begin{align}\mathsf{19_{10}} &= \mathsf{16 + 2 + 1}\\&=\mathsf{1\cdot2^4 + 1\cdot2^1 + 1\cdot2^0}\\&=\mathsf{10011_2}\end{align}\)
b) \(\begin{align}\mathsf{45_{10}} &= \mathsf{32 + 8 + 4 + 1}\\&=\mathsf{1\cdot2^5 + 1\cdot2^3 + 1\cdot2^2 + 1\cdot2^0}\\&=\mathsf{101101_2}\end{align}\)
Yleistä binääriluvuista
Ylivuoto
Ylivuodolla tarkoitetaan tilannetta, jossa luvun esittämiseen esimerkiksi tietokoneen muistissa on varattu liian vähän bittejä. Kuinka paljon on liian vähän? Kuinka suuria lukuja voi erilaisiin tavumääriin tallentaa? Oletetaan, että halutaan tallentaa positiivisia kokonaislukuja. Kuinka monta erilaista lukua voidaan tallentaa?
| Tavuja | Bittejä | Erilaisia lukuja |
|---|---|---|
| 1 | 8 | \(\mathsf{2^8 = 256}\) |
| 2 | 16 | \(\mathsf{2^{16} = 65\:536}\) |
| 4 | 32 | \(\mathsf{2^{32} = 4\:294\:967\:296}\) |
| 8 | 64 | \(\mathsf{2^{64} = 1,\!84... \cdot 10^{19}}\) |
Nämä luvut vielä puolittuvat, jos halutaan esittää negatiivisia kokonaislukuja.
Miksi pitäisi ihmisen tällaista osata ja ymmärtää?
- Yleissivistys - Muistin määrä laitteissa ilmoitetaan tavuina (8 bittiä) ja massamuistien suuruudet ovat usein jotain kahden potenssin moninkertoja (64Gt, 128Mt, 4Tt). Lisäksi internetyhteyksien tiedonsiirtonopeudet ilmoitetaan Megabitteinä sekunnissa.
- Ohjelmointi - Historiassa on havaittu ohjelmistovirheitä, jotka johtuvat ns. muistin ylivuodosta (overflow), missä luku ei ole mahtunut sille varattuun muistipaikkaan. Virheet voivat maksaa miljoonia euroja (Ariane 5) tai aiheuttaa ennakoimattomia tilanteita (Gangnam Style rikkoi YouTuben).
- Laskimet - Laskettaessa laskimella esimerkiksi suuria potenssilaskuja voi laskimen luvulle käyttämä muisti ylittyä, jolloin tulee joko väärä vastaus tai virheilmoitus.
- Desimaaliosa - Digitaaliset laitteet käyttävät binäärilukuja myös desimaalilukujen esittämiseen, jolloin käytössä on ns. liukuluvut (floating point number). Biteillä laskettaettaessa epätarkkuus, pyöristykset ja päättymättömät desimaaliluvut aiheuttavat odottamattomia virheitä.
Lukujen lisäksi binääriluvuilla tallennetaan myös muiden merkkijonojen merkit (kirjaimet, pisteet, pilkut, jne.). Netistä löytyy paljon muuntajia, joiden avulla voi merkkejä muuttaa binääriluvuiksi esimerkiksi UTF-8-merkistökoodauksen avulla.