MA8 Jakso 2: Prosenttilaskenta
1. Kertausta
Murtoluvut
Murtoluvulla esitetään kokonaisen osia. Murtoluvussa merkitään kaksi kokonaislukua allekkain, ja niiden väliin laitetaan viiva. Ylempää lukua kutsutaan osoittajaksi ja alempaa nimittäjäksi. Nimittäjä nimittää osien suuruuden ja osoittaja osoittaa kyseisten osien lukumäärän.

Murtoluku voidaan muuttaa desimaaliluvuksi, jota kutsutaan myös murtoluvun arvoksi. Murtoluku on jakolasku, joka näkyy myös yhtenevästä merkintätavastakin. Murtolukujen avulla voidaan esittää selkeästi sellaisia kokonaisen osia, jotka desimaalilukuna olisivat pitkiä tai jopa päättymättömiä.
\( \mathsf{\dfrac{1}{3} = \text{0,3333}...} \)
Näin ollen murtolukuja käytetään usein tarkkojen arvojen merkitsemiseen desimaalilukujen kärsiessä epätarkkuuden epäilyksistä mahdollisen mittaustarkkuuden tai pyöristämisen seurauksena.
Supistaminen ja laventaminen
Supistamisessa murtoluvun osoittaja ja nimittäjä jaetaan samalla luvulla, jolloin murtoluku saadaan yksinkertaisempaan muotoon. Supistettaessa murtoluvun arvo ei muutu. Supistaja merkitään kaarella murtoluvun oikeaan yläkulmaan.
Esimerkki: Supista yksinkertaisimpaan muotoon.
a) \(\mathsf{\dfrac{9}{12}^{(3} = \dfrac{3}{4}}\)
b) \(\mathsf{\dfrac{28}{36}^{(4} = \dfrac{7}{9}}\)
Laventamisessa murtoluvun osoittaja ja nimittäjä kerrotaan samalla luvulla. Lavennettaessa murtoluvun arvo ei muutu. Laventaja merkitään kaarella murtoluvun vasempaan yläkulmaan.
Esimerkki: Lavenna.
a) \(\mathsf{\rule{0pt}{1.4em}^{5)}\!\dfrac{3}{20} = \dfrac{15}{100}}\)
b) \(\mathsf{\rule{0pt}{1.4em}^{10)}\!\dfrac{5}{12} = \dfrac{50}{120}}\)
Ennen murtolukujen yhteen- tai vähennyslaskua murtolukujen tulee olla samannimiset, eli niiden nimittäjien tulee olla samat.
Vinkkejä samannimiseksi laventamiseen:
- Lavenna vain toista murtolukua, jos toinen nimittäjä on toisen moninkerta.
- Selvitä mahdollisimman pieni luku, johon molemmat nimittäjät voidaan laventaa.
\(\mathsf{\rule{0pt}{1.4em}^{2)}\!\!\dfrac{2}{15} + \!\!\rule{0pt}{1.4em}^{5)}\!\dfrac{1}{6} = \dfrac{4}{30} + \dfrac{5}{30} = \dfrac{9}{30}^{\!(3}\!\! = \dfrac{3}{10}}\) - Lavenna ristiin, jos luvut ovat pieniä tai mikään muu ei auta.
\(\mathsf{\rule{0pt}{1.4em}^{\color{red}{2})}\!\dfrac{2}{\color{blue}{3}} - \rule{0pt}{1.4em}^{\color{blue}{3})}\dfrac{1}{\color{red}{2}} = \dfrac{4}{6} - \dfrac{3}{6} = \dfrac{1}{6}}\)
Summa ja erotus
Laskettaessa murtolukuja yhteen, murtolukujen tulee olla samannimiset. Yhteenlaskussa osoittaja lasketaan yhteen, mutta nimittäjät pysyvät samana. Tämä on ilmeistä, sillä laskettaessa esimerkiksi viidesosia yhteen, saadaan vastaukseksi tietenkin viidesosia.
Esimerkki: Laske.
a) \(\mathsf{\dfrac{2}{5} + \dfrac{1}{5} = \dfrac{3}{5}}\)
b) \(\mathsf{\rule{0pt}{1.4em}^{2)}\!\color{blue}{\dfrac{1}{5}} + \color{red}{\dfrac{7}{10}} = \color{blue}{\dfrac{2}{10}} + \color{red}{\dfrac{7}{10}} = \dfrac{9}{10}}\)
Toimintaohje murtolukujen yhteen- ja vähennyslaskuun:
- Muunna murtoluvut samannimisiksi, jos on tarpeen.
- Laske lasku osoittajilla.
- Nimittäjä pysyy samana.
- Supista vastaus, jos mahdollista.
- Muuta sekaluvuksi, jos mahdollista.
Tulo ja osan ottaminen luvusta
Vanhastaan tiedetään, että kertolasku on lyhyempi tapa kirjoittaa toistuva yhteenlasku. Tämän perusteella voidaan johtaa laskusääntö kertolaskulle myös murtolukujen tapauksessa.
\(\mathsf{3 \cdot \dfrac{2}{5} \,=\, \dfrac{2}{5} + \dfrac{2}{5} + \dfrac{2}{5} \,=\, \dfrac{6}{5}}\)
Kuten huomataan, kertolasku on kohdistunut vain osoittajaan \(\mathsf{3 \cdot 2 = 6}\), mut nimittäjä on pysynyt samana. Murtoluvun ja kokonaisluvun kertolasku voidaan siis ajatella myös näin.
\(\mathsf{3 \cdot \dfrac{2}{5} \,=\, \dfrac{3\cdot 2}{5} \,=\, \dfrac{6}{5}}\)
Käytännössä kokonaisluvun ja murtoluvun välistä kertolaskua käytetään sellaisessa käytännön tilanteessa, missä halutaan ottaa tietyn suuruinen osa jostakin kokonaisuudesta.
Esimerkki: Kuinka paljon on \(\mathsf{\small\dfrac{3}{5}}\) 35 eurosta?
\( \mathsf{\dfrac{3}{5} \cdot \text{35 €} = \text{21 €}} \)
Miksi kertolaskua käytetään osan ottamiseen? Tarkastellaan lyhyttä esimerkkiä suklaalevystä.
Esimerkki:
a) Suklaalevyssä on 24 palaa. Kuinka monta palaa on kolmessa suklaalevyssä.
\(\mathsf{3 \cdot 24 = 72}\)
Vastaus: Kolmessa levyssä on 72 palaa.
b) Suklaalevyssä on 24 palaa. Kuinka monta palaa on yksi kolmasosa suklaalevystä.
\(\mathsf{\dfrac{1}{3} \cdot 24 = 8}\)
Vastaus: Kolmasosa suklaalevystä on 8 palaa.
Kuten huomataan, kokonaisuus voidaan kertolaskun avulla moninkertaistaa tai saada osiin kun valitaan sopiva kerroin. Tämä ajatus siirretään myöhemmin suoraan prosenttilaskentaan, joten osan ottaminen luvusta kertolaskun avulla on hyvä painaa mieleen.
Murtolukujen muuntaminen desimaaliluvuiksi
Desimaaliluvut ovat toinen tapa merkitä kokonaisen osia. Desimaaliluvussa merkitään kokonaisten jälkeen pilkku, ja sen jälkeen kymmenesosat, sadasosat, tuhannesosat, jne. omilla paikoillaan. Tämän vuoksi on tärkeätä opetella desimaalilukujen ja murtolukujen väliset muunnokset.
Murtoluvut, joissa on nimittäjänä jokin kymmenen moninkerta, vastaavat suoraan desimaalilukuja.
Esimerkki: Muunna desimaaliluvuksi.
a) \(\mathsf{\dfrac{8}{10} = \text{0,8}}\)
b) \(\mathsf{\dfrac{5}{100} = \text{0,05}}\)
c) \(\mathsf{\dfrac{34}{100} = \text{0,34}}\)
d) \(\mathsf{\dfrac{93}{1000} = \text{0,093}}\)
Jos murtoluvun nimittäjä ei ole kymmenen moninkerta, se voidaan yrittää laventaa johonkin niistä.
Esimerkki: Muunna desimaaliluvuksi.
a) \(\mathsf{\rule{0pt}{1.4em}^{2)}\!\dfrac{3}{5} = \dfrac{6}{10} = \text{0,6}}\)
b) \(\mathsf{\rule{0pt}{1.4em}^{25)}\!\dfrac{1}{4} = \dfrac{25}{100} = \text{0,25}}\)
c) \(\mathsf{\rule{0pt}{1.4em}^{5)}\dfrac{1}{20} = \dfrac{5}{100} = \text{0,05}}\)
Jos laventaminen tai päässälasku ei onnistu, niin viimeinen keino on laskea murtolukua vastaava jakolasku laskimella.
\(\mathsf{\dfrac{8}{11} = \text{0,727272}...}\)
Desimaalilukujen kertominen ja jakaminen kymmenen moninkerroilla
Kymmenen moninkerroilla kerrottaessa desimaaliluvussa pilkku siirtyy oikealle nollien osoittaman määrän verran.
Esimerkki: Laske.
a) \(\mathsf{\text{3,14} \cdot 10 = \text{31,4}}\)
b) \(\mathsf{\text{3,14} \cdot 100 = 314}\)
c) \(\mathsf{\text{3,14} \cdot 1000 = \text{3 140}} \)
Jos numerot, joiden yli pilkkua voidaan siirtää, loppuvat kesken, lisätään tarvittaessa luvun loppuun nollia.
Jaettaessa kymmenen moninkerroilla pilkku siirtyy puolestaan vasemmalle. Tällöin saattaa ilmetä tarve lisätä nollia luvun eteen pilkun siirtämisen mahdollistamiseksi.
Esimerkki: Laske.
a) \(\mathsf{\text{78,3} : 10 = \text{7,83}}\)
b) \(\mathsf{\text{78,3} : 100 = \text{0,783}}\)
c) \(\mathsf{\text{78,3} : 1000 = \text{0,0783}} \)
2. Prosentti
Prosentti (lat. per centum, sataa kohti tai pro centum, sadasta) on yhteisesti sovittu nimitys sadasosalle. Prosenttia merkitään %-merkillä. Kokonaiseen mahtuu siis aina 100 %. Tilanteesta riippuen tämä kokonainen voi vaihdella, ja siksi on hyvä muistaa, että prosentti kuvaa siis suhteellista osuutta jostakin, eikä tilanteesta toiseen siirryttäessä voida olettaa esimerkiksi yhden prosentin vastaavan samaa euromäärää, painoa, äänimäärää tai pituutta.
Käsitteitä
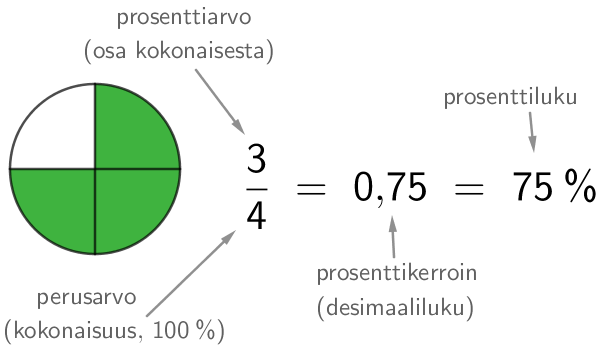
Sadasosia on opittu aiemmin merkitsemään murtolukuina sekä desimaalilukuina, joten kolmanneksi tavaksi saadaan nyt prosenttiluku. Prosenttiluvun desimaalimuotoa kutsutaan prosenttikertoimeksi. Prosenttiluku mitataan aina suhteessa johonkin kokonaisuuteen eli perusarvoon. Prosenttilukua vastaava osuus perusarvosta on nimeltään prosenttiarvo.
Esimerkki: Kirjoita väritetyn osan suuruus murtolukuna, desimaalilukuna sekä prosenttilukuna.
3. Prosentteja päässälaskuna
Valtaosa arkielämän prosenttilaskuista tapahtuu päässälaskuna esimerkiksi ostoksia tehtäessä. Tuote voi olla 20 % alennuksessa, tuotteen hintaan sisältyy 24 % arvonlisävero, tuotteessa on 0,8 % suolaa tai siinä mainoksen mukaan 30 % vähemmän sokeria kuin ennen.
Päässälaskun helpottamiseksi sekä prosenttilaskennan ymmärtämiseksi käytetään apuna taulukkoa, johon syötetään tunnetut tiedot sekä prosentteina että varsinaisina mitattavina suureina (eurot, metrit, klogrammat, kappalemäärät, jne.). Puuttuvia taulukon lukuja voidaan laskea usein yksinkertaisilla päässälaskuilla.
Esimerkki: Suklaalevyssä on 24 palaa. Muodosta taulukko, ja laske, kuinka monta palaa suklaalevystä on
a) 25 %
b) 50 %
c) 75 %
Tehtävästä riippuen taulukosta voi jäädä tyhjäksi (tuntemattomaksi) mikä tahansa ruutu, kunhan jokin luku-prosenttipari on ennalta tunnettu. Tarkatellaan vielä kahta esimerkkiä.
Esimerkki: Luokalla on normaalisti 25 oppilasta, mutta nyt 5 oppilasta on pois koulusta sairastumisen vuoksi. Kuinka monta prosenttia oppilaista on pois koulusta?
Esimerkki: Koe hylätään, jos kokeesta saa vähemmän kuin 30 % pisteistä. Pekka sai kokeesta 12 pistettä. Mikä pitäisi kokeen kokonaispistemäärän vähintään olla, että Pekka ei saisi hylättyä arvosanaa?
4. Prosenttilaskennan perustapaukset
Prosenttilaskennassa on havaittavissa kolme perustapausta. Perustapauksia on kolme, koska perustilanteissa on kolme suuretta (perusarvo, prosenttiarvo sekä prosenttiluku), joista yksi on vuorollaan tuntematon, ja kaksi muuta täytyy tuntea. Käytännössä kaikki myöhemmät prosenttitehtävät pohjautuvat näihin kolmeen perustapaukseen. Toisaalta tuntemalla yhden tapauksen, voidaan muut johtaa yhtälönratkaisun keinoin.
1. Prosenttiluvun laskeminen
Kuinka monta prosenttia 12 euroa on 40 eurosta?
\(\mathsf{\dfrac{\text{12 €}}{\text{40 €}} = \text{0,3} = \text{30 %}}\)
2. Prosenttiarvon laskeminen
Kuinka paljon on 56 % 75 eurosta?
\(\mathsf{\text{56 %} = \text{0,56}}\)
\(\mathsf{\text{0,56} \cdot \text{75 €} = \text{42 €}}\)
3. Perusarvon ratkaiseminen
Mistä hinnasta 24 % on 84 euroa?
\(\mathsf{\text{24 %} = \text{0,24}}\)
\(\mathsf{\dfrac{\text{84 €}}{\text{0,24}} = \text{350 €}}\)
Prosenttiluvun laskeminen
Kuten luvun 2 määritelmässä havaittiin, voidaan osa kokonaisuudesta ilmoittaa murtolukuna, desimaalilukuna sekä prosenttilukuna. Tästä saadaan suoraan laskukaava prosenttiluvun laskemiseksi.
\(\mathsf{\dfrac{Osa}{Kokonainen} = \%_{kerroin} = Prosenttiluku}\)
Esimerkki: Luokalla on 7 poikaa ja 13 tyttöä. Kuinka monta prosenttia oppilaista on poikia?
Poikia (osa): \(\mathsf{7}\)
Oppilaita yhteensä (kokonainen): \(\mathsf{7 + 13 = 20}\)
Poikien määrä prosentteina (prosenttiluku): \(\mathsf{\dfrac{7}{20} = \text{0,35} = \text{35 %}}\)
Jos kysymys siis kuuluu "Kuinka monta prosenttia...":
- Muodosta murtoluku (eli jakolasku)
- Laske jakolasku (saat prosenttikertoimen)
- Muunna prosenttiluvuksi (kerro sadalla)
Prosenttiarvon laskeminen
Murtolukujen puolelta muistetaan tilanne, jossa jostakin kokonaisuudesta otettiin haluttu osa kertomalla kyseinen kokonaisuus osaa kuvaavalla murtoluvulla.
Esimerkki: Laske \(\mathsf{\dfrac{3}{4}}\) 36 eurosta.
\(\mathsf{\dfrac{3}{4} \cdot \text{36 €} = \text{27 €}}\)
Sama tehtävä voitaisiin antaa prosenttitehtävänä, jos muutetaan murtoluku prosenteiksi, eli prosenttiluvuksi (\(\mathsf{\small\dfrac{3}{4}\normalsize = \text{75 %}}\)). Jotta prosenttiluvulla voidaan kertoa, on se muutettava ennen laskemista prosenttikertoimeksi, eli desimaaliluvuksi. Prosenttikertoimeksi muuttaminen tapahtuu siis jakamalla prosenttiarvo luvulla 100, koska prosentti tarkoitti nimenomaan sadasosaa.
Esimerkki: Kuinka paljon on 75 % 36 eurosta.
\(\mathsf{\text{75 %} = \text{0,75}}\)
\(\mathsf{\text{0,75} \cdot \text{36 €} = \text{27 €}}\)
Tästä saadaan laskukaava toiseen prosenttilaskennan perustapaukseen, eli prosenttiarvon laskemiseen. Tästä laskukaavasta käytetään myöhemmin myös nimitystä prosenttiyhtälö, koska siitä voidaan helposti ratkaista muut prosenttilaskennan laskukaavat.
\(\mathsf{\%_{kerroin}} \cdot \textsf{Kokonainen} = \textsf{Osa}\)
Jos kysymys siis kuuluu "Kuinka paljon...":
- Muunna prosenttiluku prosenttikertoimeksi (jaa sadalla)
- Muodosta kertolasku (prosenttikerroin kertaa kokonaisuus)
- Laske kertolasku
Perusarvon laskeminen
Perusarvon, eli kokonaisuuden (100 %) laskeminen on luvussa 4.2. esitetyn prosenttiarvon laskukaavan käänteinen tapaus. Käänteiset tapaukset voidaan ratkaista helposti yhtälönratkaisun avulla. Nimetään luvun 4.2. prosenttiarvon laskukaava prosenttiyhtälöksi.
\(\mathsf{\%_{kerroin} \cdot Kokonainen = Osa}\)
Ratkaistaan yhtälöstä kokonainen jakamalla prosenttikertoimella.
\(\begin{align}\mathsf{\%_{kerroin} \cdot Kokonainen} &= \mathsf{Osa} && \mathsf{\| : \%_{kerroin}}\\ \quad\\ \mathsf{Kokonainen} &= \mathsf{\dfrac{Osa}{\%_{kerroin}}}\end{align}\)
Näin ollen perusarvolle saadaan laskukaavaksi
\(\mathsf{Kokonainen = \dfrac{Osa}{\%_{kerroin}}}\)
Esimerkki: Banaanissa on 9 grammaa proteiinia, joka vastaa 6 prosenttia banaanin massasta. Kuinka paljon banaani painaa?
\(\textsf{6 % = 0,06}\)
\(\mathsf{\dfrac{\text{9 g}}{\text{0,06}} = \text{150 g}}\)
Vastaus: Banaani painaa 150 grammaa.
Jos kysymys on muotoa "Mistä kokonaisuudesta..."
- Muuta prosenttiluku prosenttikertoimeksi
- Muodosta jakolasku (osa kokonaisuudesta jaettuna prosenttikertoimella)
- Laske jakolasku
5. Muutos prosentteina
Prosentteja käytetään muutoksen ilmaisemiseen. Alkuperäinen arvo vastaa aina 100 prosenttia. Muuttunut arvo voi olla alkuperäistä suurempi tai pienempi, riippuen muutoksen suunnasta. Muutos on muuttuneen arvon ja alkuperäisen arvon erotus. Muutosprosentti on siis muutoksen suhde alkuperäiseen arvoon.
Muutosprosentin laskeminen
Muutosprosentin laskeminen vastaa kysymykseen "Kuinka monta prosenttia muutos on alkuperäisestä?".
\(\mathsf{\dfrac{Muutos}{Alkuperäinen} = \%_{kerroin} = Muutosprosentti}\)
Esimerkki: Työntekijän alkuperäinen kuukausipalkka on 3 440 euroa. Hän saa kuukausipalkkaan 86 euron palkankorotuksen. Kuinka monta prosenttia palkankorotus on?
Muutos: \(\mathsf{\text{86 €}}\)
Alkuperäinen: \(\mathsf{\text{3 440 €}}\)
Muutosprosentti: \(\mathsf{\dfrac{\text{86 €}}{\text{3 440 €}} = \text{0,025} = \text{2,5 %}}\)
Vastaus: Palkankorotus on 2,5 %.
Ennen muutosprosentin laskemista, tulee tietää muutoksen suuruus. Jos muutosta ei ole etukäteen tiedossa, se täytyy laskea vähennyslaskun avulla.
Esimerkki: Tuotteen alkuperäinen hinta on 60 euroa. Alennusmyynnissä tuotteen saa 39 eurolla. Kuinka monta prosenttia hinta laskee?
Muutos: \(\mathsf{\text{60 €} - \text{39 €} = \text{21 €}}\)
Muutosprosentti: \(\mathsf{\dfrac{\text{21 €}}{\text{60 €}} = \text{0,35} = \text{35 %}}\)
Vastaus: Hinta laskee 35 prosenttia.
Muutoksen ja muuttuneen arvon laskeminen
Jos muutosprosentti tunnetaan, voidaan muutoksen todellinen suuruus laskea kertomalla alkuperäistä arvoa prosenttikertoimella. Muuttunut arvo voidaan laskea tämän jälkeen lisäämällä/vähentämällä muutos alkuperäiseen. Jos tarkoituksena on nimenomaan selvittää muuttunut arvo, voidaan ensin selvittää muuttuneen arvon prosenttiosuus alkuperäisestä, ja laskea muuttunut arvo suoraan.
\(\mathsf{\%_{kerroin}} \cdot \textsf{Alkuperäinen}= \textsf{Muutos}\)
Esimerkki: Tuotteen alkuperäinen hinta on 9,90 euroa. Tuote myydään 30 prosentin alennuksella. Kuinka paljon alennus on euroina?
Prosenttikerroin: \(\mathsf{\text{30 %} = \text{0,3}}\)
Muutos: \(\mathsf{\text{0,3} \cdot \text{9,90 €} = \text{2,97 €}}\)
Vastaus: Alennus on 2,97 euroa.
Esimerkki: Tuotteen veroton (alkuperäinen) hinta on 32,50 euroa. Tuoteeseen lisätään arvonlisävero (ALV), joka on 24 % tuoteen verottomasta hinnasta. Kuinka paljon tuote maksaa lisäyksen jälkeen?
Tapa 1:
Prosenttikerroin: \(\mathsf{\text{24 %} = \text{0,24}}\)
Muutos: \(\mathsf{\text{0,24} \cdot \text{32,50 €} = \text{7,80 €}}\)
Uusi hinta: \(\mathsf{\text{32,50 €} + \text{7,80 €} = \text{40,30 €}}\)
Vastaus: Tuote maksaa 40,30 euroa.
Tapa 2:
Uusi hinta prosentteina:
\(\mathsf{\text{100 %} + \text{24 %} = \text{124 %}}\)
Prosenttikerroin: \(\mathsf{\text{124 %} = \text{1,24}}\)
Uusi hinta: \(\mathsf{\text{1,24} \cdot \text{32,50 €} = \text{40,30 €}}\)
Vastaus: Tuote maksaa 40,30 euroa.
Alkuperäisen arvon laskeminen
Alkuperäisen arvon laskeminen vastaa aiemmin opittua perusarvon laskemista. Sen laskukaava voidaan johtaa myös samaan tapaan muutoksen laskukaavasta yhtälönratkaisun avulla.
\(\begin{align}\mathsf{\%_{kerroin}} \cdot \textsf{Alkuperäinen} &= \textsf{Muutos} && \mathsf{\|:\%_{kerroin}}\\\rule{5pt}{0em}\\\textsf{Alkuperäinen} &= \mathsf{\dfrac{Muutos}{\%_{kerroin}}}\end{align}\)
Tästä saadaan alkuperäiselle arvolle laskukaava.
\(\mathsf{Alkuperäinen = \dfrac{Muutos}{\%_{kerroin}}}\)
Esimerkki: Uuno sai 2 prosentin palkankorotuksen, joka vastaa 55 euroa. Mikä oli Uunon alkuperäinen palkka?
Prosenttikerroin: \(\mathsf{\text{2 %} = \text{0,02}}\)
Alkuperäinen palkka: \(\mathsf{\dfrac{\text{55 €}}{\text{0,02}} = \text{2 750 €}}\)
Vastaus: Uunon alkuperäinen palkka oli 2750 euroa.
Esimerkki: 25 prosentin alennuksen jälkeen kengistä jäi maksettavaa 126 euroa. Mikä oli kenkien alkuperäinen hinta?
Hinta prosentteina alennuksen jälkeen: \(\mathsf{\text{100 %} - \text{25 %} = \text{75 %}}\)
Prosenttikerroin: \(\mathsf{\text{75 %} = \text{0,75}}\)
Alkuperäinen hinta: \(\mathsf{\dfrac{\text{126 €}}{\text{0,75}} = \text{168 €}}\)
Vastaus: Kenkien alkuperäinen hinta oli 168 euroa.
Muutos prosenttiyksikköinä
Muutosta voidaan tarkastella myös vertailemalla prosenttilukuja toisiinsa. Tällöin prosenttia käytetään yksikkönä, eli samaan tapaan kuin metrejä, sekunteja tai kilogrammoja. Prosenttiyksiköitä voidaan käyttää esimerkiksi vaaleissa ja äänestyksissä tarkasteltaessa ehdokkaan suhteellisen äänimäärän muutosta eri vuosina, tai vertailtaessa kahta puoluetta toisiinsa.
Esimerkki: Arttu sai joukkueen kapteeniäänestyksessä 45 % äänistä vuonna 2020 ja 57 % äänistä vuonna 2021. Kuinka monta prosenttiyksikköä Artun äänimäärä kasvoi?
Prosenttilukujen erotus: \(\mathsf{\text{57 %} - \text{45 %} = \text{12 %}}\)
Vastaus: Artun äänimäärä kasvoi 12 prosenttiyksikköä.
Prosenttiyksiköiden avulla ei siis lasketa suhteellista muutosta vaan verrataan vain prosenttilukuja toisiinsa. Prosenttilukujen avulla voidaan toki laskea myös suhteellinen muutos, ja tällöin toimitaan aiemmin opitulla tavalla.
Esimerkki: Arttu sai joukkueen kapteeniäänestyksessä 45 % äänistä vuonna 2020 ja 57 % äänistä vuonna 2021. Kuinka monta prosenttia Artun äänimäärä kasvoi?
Muutos: \(\mathsf{\text{57 %} - \text{45 %} = \text{12 %}}\)
Suhteellinen muutos: \(\mathsf{\dfrac{\text{12 %}}{\text{45 %}} = \text{0,2666}... \approx \text{27 %}}\)
Vastaus: Artun äänimäärä kasvoi 27 prosenttia.
6. Vertailu prosentteina
Kahden asian suuruutta voidaan vertailla toisiinsa prosenttien avulla. Vertailutehtävissä kokonaisuutta edustaa vertailun kohde, eli se suure johon toista verrataan. Suomen kielessä käytetään usein sanaaa "kuin" ilmoittamaan vertailun kohde. Tämä voi helpottaa sanallisten tehtävien ratkaisemista.
Vertailuprosentti
Ennen vertailuprosentin laskemista tulee selvittää vertailtavien kohteiden suuruusero. Jos suuruusero ei ole etukäteen tiedossa, voidaan se laskea vähennyslaskun avulla. Käytännössä vertailuprosentin laskeminen vastaa kysymykseen "Kuinka monta prosenttia suuruusero on vertailun kohteesta?".
\(\mathsf{\dfrac{Suuruusero}{\text{Vertailun kohde}} = \%_{kerroin} = Vertailuprosentti}\)
Esimerkki: Pekalla on rahaa 60 euroa, ja Lassella on rahaa 72 euroa. Kuinka monta prosenttia Lassella on enemmän rahaa kuin Pekalla.
Vertailun kohde: \(\mathsf{\text{60 €}}\) (Pekka)
Suuruusero: \(\mathsf{\text{72 €} - \text{60 €} = \text{12 €}}\)
Vertailuprosentti: \(\mathsf{\dfrac{\text{12 €}}{\text{60 €}} = \text{0,20} = 20 \:\%}\)
Vastaus: Lassella on 20 % enemmän rahaa kuin Pekalla.
Suuruuseron laskeminen
Jos vertailuprosentti ja vertailun kohde tunnetaan, voidaan laskea vertailtavien kohteiden suuruusero. Jos tarkoituksena on laskea toisen vertailtavan kohteen suuruus, voidaan suuruusero lisätä/vähentää joko ennen tai jälkeen varsinaisen prosenttilaskun.
\(\mathsf{\%_{kerroin}} \cdot \textsf{Vertailun kohde}= \textsf{Suuruusero}\)
Esimerkki: Tanja on 158 cm pitkä. Riina on 7 prosenttia pidempi kuin Tanja. Kuinka paljon Riina on pidempi kuin Tanja?
Vertailun kohde: \(\mathsf{158\:cm}\) (Tanja)
Vertailuprosentti ja -kerroin: \(\mathsf{\text{7 %} = \text{0,07}}\)
Suuruusero:
\(\mathsf{\text{0,07} \cdot \text{158 cm} = \text{11,06 cm} \approx \text{11 cm}}\)
Vastaus: Riina on 11 cm pidempi kuin Tanja.
Jos tehtävässä kysytään toisen vertailtavan suuruutta eikä vain suuruuseroa. Meillä on jälleen kaksi tapaa ratkaista tehtävä. Suuruusero voidaan lisätä/vähentää vertailun kohteesta lopuksi (Tapa 1) tai suuruuseroa vastaava prosenttiluku voidaan lisätä/vähentää 100 prosentista heti aluksi (Tapa 2).
Esimerkki: Älypuhelin maksaa Terantti-myymälässä 225 euroa. Force-myymälä myy samaa älypuhelinta 8 prosenttia halvemmalla. Kuinka paljon puhelin maksaa Force-myymälässä?
Tapa 1:
Prosenttikerroin: \(\mathsf{\text{8 %} = \text{0,08}}\)
Suuruusero: \(\mathsf{\text{0,08} \cdot \text{225 €} = \text{18 €}}\)
Uusi hinta: \(\mathsf{\text{225 €} - \text{18 €} = \text{207 €}}\)
Tapa 2:
Uusi hinta prosentteina: \(\mathsf{\text{100 %} - \text{8 %} = \text{92 %}}\)
Prosenttikerroin: \(\mathsf{\text{92 %} = \text{0,92}}\)
Uusi hinta: \(\mathsf{\text{0,92} \cdot \text{225 €} = \text{207 €}}\)
Vastaus: Älypuhelin maksaa Force-myymälässä 207 euroa.
Vertailun kohteen laskeminen
Vertailun kohteen laskeminen vastaa aiemmin opittua perusarvon laskemista, eli kokonaisuus (100 %) on tuntematon.
\(\mathsf{\text{Vertailun kohde} = \dfrac{Suuruusero}{\%_{kerroin}}}\)
Esimerkki: Ruotsissa on 86 prosenttia enemmän asukkaita kuin Suomessa. Tämä vastaa 4,8 miljoonaa asukasta. Kuinka paljon Suomessa on asukkaita?
Suuruusero: \(\mathsf{\text{4,8}}\) milj. asukasta.
Vertailuprosentti ja -kerroin: \(\mathsf{86 \:\% = \text{0,86}}\)
Vertailun kohde: \(\mathsf{\dfrac{\text{4,8}}{\text{0,86}} = \text{5,58}... \approx \text{5,6}}\)
Vastaus: Suomessa on 5,6 miljoonaa asukasta.
Esimerkki: Otso heitti keihästä 20 prosenttia vähemmän kuin Reijo. Otso heitti 56 metriä. Kuinka paljon Reijo heitti keihästä?
Vertailuprosentti ja -kerroin:
\(\mathsf{100 \:\% - \text{20 %} = \text{80 %} = \text{0,8}}\)
Vertailun kohde: \(\mathsf{\dfrac{56}{\text{0,8}} = 70}\)
Vastaus: Reijo heitti keihästä 70 metriä.
7. Verot
Yhteiskunnan toimintaa rahoitetaan keräämällä erilaisia veroja. Palkasta maksetaan mm. tuloveroa ja kunnallisveroa, ostoksista arvonlisäveroa (ALV), polttoaineesta polttoaineveroa, perinnöstä perintöveroa ja suurista lahjoista lahjaveroa.
Arvonlisävero
Suomessa yleinen arvonlisäveroprosentti on 25,5 %. Tuotteen myyvä yritys lisää tuotteen hintaan arvonlisäveron.
Esimerkki: Älykellon veroton hinta on 180 euroa. Mikä on älykellon myyntihinta?
Prosenttikerroin:
\(\mathsf{\text{100 %} + \text{25,5 %} = \text{125,5 %} = \text{1,255}}\)
Myyntihinta:
\(\mathsf{\text{1,255} \cdot \text{180 €} = \text{225,90 €}}\)
Vastaus: Älykellon myyntihinta on 225,90 euroa.
Veroton hinta vastaa siis kokonaisuutta eli 100 prosenttia. Jos ongelma on käänteinen, eli kysytään verotonta hintaa, tulee myyntihinta jakaa sitä vastaavalla prosenttikertoimella 1,255.
Esimerkki: Kenkien myyntihinta on 112,95 euroa. Mikä on kenkien veroton hinta?
Prosenttikerroin:
\(\mathsf{\text{100 %} + \text{25,5 %} = \text{125,5%} = \text{1,255}}\)
Veroton hinta:
\(\mathsf{\dfrac{\text{112,95 €}}{\text{1,255}} = \text{90,00 €}}\)
Vastaus: Tuotteen veroton hinta on 90,00 euroa.
Muita arvonlisäveroprosentteja löydät esimerkiksi Veronmaksajat.fi-sivustolta
Ansiotulovero
Ansiotulot
Palkkatuloista maksetaan veroja sekä sosiaalivakuutusmaksuja. Palkkatulojen verotus muodostuu mm. valtion-, kunnallis- ja kirkollisverosta sekä Yle-verosta. Sosiaalivakuutusmaksut sisältävät sairaanhoito- ja päivärahamaksun sekä työttömyysvakuutusmaksun ja työeläkemaksun. Ansiotulo ennen verojen maksamista on ns. bruttopalkka, ja verojen jälkeen "käteen" jäävä osuus on ns. nettopalkka. Bruttopalkasta tehdään erilaisia vähennyksiä ennen kunkin veron maksamista, joka tekee laskukaavoista ja menetemistä mutkikkaita.
Esimerkki: Jarin ansiotulot (bruttopalkka) on 3 550 euroa kuukaudessa. Mitkä ovat on Jarin ansiotulot vuodessa?
\(\mathsf{12 \cdot \text{3 550 €} = \text{42 600 €}}\)
Vastaus: Jarin ansiotulot vuodessa ovat 42 600 euroa.
Sosiaalivakuutusmaksut
Ansiotuloista maksetaan, ja myöhempää verotusta varten vähennetään seuraavat sosiaalivakuutusmaksut:
- Eläkevakuutusmaksut (7,15 %)
- Työttömyysvakuutusmaksut (0,79 %)
- Sairausvakuutusmaksun päivärahamaksu (1,01 %)
Esimerkki: Kuinka paljon Jari maksaa sosiaalivakuutusmaksuja 42 600 euron ansiotuloistaan?
Maksut yhteensä (%):
\(\mathsf{\text{7,15 %} + \text{0,79 %} + \text{1,01 %} = \text{8,95 % }}\)
Prosenttikerroin: \(\mathsf{\text{8,95 %} = \text{0,0895}}\)
Maksut yhteensä (€):
\(\mathsf{\text{0,0895} \cdot \text{42 600 €} = \text{3 812,70 €}}\)
Vastaus: Jari maksaa sosiaalivakuutusmaksuja 3 812,70 euroa.
Valtion tulovero
Valtionverotuksessa verotettavana tulona käytetään tuloja, jotka jäävät jäljelle kun ansiotuloista on vähennetty sosiaalivakuutusmaksut.
Esimerkki: Kuinka paljon verotettavaa tuloa Jarilla on valtionverotuksessa?
Ansiotulo: \(\mathsf{\text{42 600 €}}\)
Sosiaalivakuutusmaksut: \(\mathsf{\text{3 812,70 €}}\)
Verotettava tulo:
\(\mathsf{\text{42 600 €} - \text{3 812,70 €} = \text{38 787,30 €}}\)
Vastaus: Jarilla on verotettavaa tuloa valtionverotuksessa on 38 787,30 euroa.
Tulovero määräytyy valtion tuloveroasteikon mukaan.
| Vuoden 2024 tuloveroasteikko | ||
|---|---|---|
| Verotettava ansiotulo | Vero alarajan kohdalla | Vero alarajan ylittävästä tulon osasta |
| 0 € - 20 500 € | 0,00 € | 12,64 % |
| 20 500 € - 30 500 € | 2 591,20 € | 19,00 % |
| 30 500 € - 50 400 € | 4 491,20 € | 30,25 % |
| 50 400 € - 88 200 € | 10 510,95 € | 34,00 % |
| 88 200 € - 150 000 € | 23 362,95 € | 42,00 % |
| 150 000 € - | 49 318,95 € | 44,00 % |
Esimerkki: Kuinka paljon Jarin 38 787,30 euron verotettavista tuloista pitäisi maksaa tuloveroa?
Jarin verotettavat tulot ovat 38 787,30 euroa, joten käytetään taulukon kolmatta riviä.
Vero alarajan kohdalla:
\(\textsf{4 491,20 €}\)
Alarajan ylittävä osa:
\(\mathsf{\text{38 787,30 €} - \text{30 500 €} = \text{8 287,30 €}}\)
Veroprosentin prosenttikerroin:
\(\mathsf{\text{30,25 %} = \text{0,3025}}\)
Vero alarajan ylittävästä osasta:
\(\mathsf{\text{0,3025} \cdot \text{8 287,30 €} = \text{2 506,908... €}}\)
Tulovero yhteensä:
\(\begin{align}\mathsf{\text{4 491,20 €} + \text{2 506,908... €}} &= \textsf{6 998,108... €}\\ &\approx \textsf{6 998,11 €}\end{align}\)
Vastaus: Jari maksaa tuloveroa 6 998,11 euroa.
Kunnallisvero
Kunnallisveron suuruus riippuu asuinkunnasta, ja on keskimäärin noin 9 prosenttia.
Esimerkki: Laske Jarin maksama kunnallisvero, kun Jari asuu Ylöjärvellä, missä kunnallisveroprosentti vuonna 2024 on 8,4 prosenttia? Käytetään Jarin verotettavina tuloina 38 787,30 euroa.
Kunnallisvero:
\(\begin{align}\mathsf{\text{0,084} \cdot \text{38 787,30 €}} &= \textsf{3 258,133... €}\\ &\approx \textsf{3 258,13 €}\end{align}\)
Vastaus: Jarin maksaa kunnallisveroa 3 258,13 euroa.
Sosiaalivakuutusmaksut-kohdassa todettiin, että sairausvakuutusmaksujen sairaanhoitomaksut maksetaan kunnallisverotuksen verotettavasta ansiotulosta. Vuonna 2024 sairaanhoitomaksu oli 0,51 prosenttia.
Esimerkki: Kuinka paljon Jari maksaa sairausvakuutusmaksun sairaanhoitomaksua?
Verotettava tulo kunnallisverotuksessa:
\(\mathsf{\text{38 787,30 €}}\)
Sairaanhoitomaksu:
\(\begin{align}\mathsf{\text{0,0051} \cdot \text{38 787,30 €}} &= \textsf{197,815... €}\\ &\approx \textsf{197,82 €}\end{align}\)
Vastaus: Jari maksaa sairaanhoitomaksua 197,82 euroa.
8. Korot
Talletuksista ja lainoista maksetaan korkoa. Jos talletat rahaa pankkiin, pankki maksaa talletuksestasi korkoa. Jos taas ostat asunnon tai auton, niin voit lainata rahaa pankilta, jolloin maksat lainatusta rahasta korkoa.
Pankkitilien korot
Pankkitilien korot vaihtelevat pankeittain, ja riippuvat myös tilin tyypistä. Korkojaksolla tarkoitetaan ajanjaksoa, jolta korko lasketaan. Yleisesti korkojakso on yksi vuosi. Laina-aika voi olla tätä pidempikin, mutta korko lasketaan ja maksetaan yleensä vuosittain. Korkokanta voi olla kiinteä tai vaihtuva, eli se riippuu jostakin viitekorosta.
Käyttötilillä tarkoitetaan tiliä, josta tehdään paljon nostoja ja talletuksia. Suomalaisilla pankeilla käyttötilien korot ovat tällä hetkellä 0 - 1 prosenttia. Siksi ne sopivatkin arkipäivän rahaliikenteeseen, mutta eivät pitkäaikaisempaan säästämiseen.
Säästötilille on tarkoitus tehdä pitkäaikaisempia talletuksia, eikä sieltä ole tarkoitus nostaa rahoja pois kuin harvakseltaan. Yleisesti säästötilien korot ovat käyttötilejä korkeampia, mutta huonoina talousaikoina korot voivat olla hyvin lähellä nollaa. Tilityyppejä on erilaisia ja lopulliseen korkoon vaikuttaa nostojen määrä, talletuksen suuruus sekä talletusaika.
Esimerkki: Matti tallettaa 1 500 euroa SVEA-säästötilille, jonka korkokanta on 3,55 %. Kuinka paljon talletukselle maksetaan korkoa ensimmäisenä vuonna?
Prosenttikerroin: \(\mathsf{\text{3,55 %} = \text{0,0355}}\)
Korko: \(\mathsf{\text{0,0355} \cdot \text{1 500 €} = \text{53,25 €}}\)
Vastaus: Talletukselle maksetaan korkoa 53,25 euroa.
Korkoa korolle
Säästötilin summa kasvaa vuosittain talletuskoron verran, jolloin seuraavana vuonna korkotuotto on aina edellistä suurempi. Korkoa vastaavalla prosenttikertoimella kerrotaan siis aina edellisen vuoden saldoa uudestaan ja uudestaan.
Esimerkki: Kuinka paljon edellisen esimerkin Matilla on säästötilillään rahaa 10 vuoden kuluttua?
Prosenttikerroin:
\(\mathsf{\text{100 %} + \text{3,55 %} = \text{103,55 %} = \text{1,0355}}\)
| Vuosi | Tilin saldo (€) | Tilin saldo koron jälkeen (€) |
|---|---|---|
| 1 | 1 500,00 | \(\mathsf{\text{1,0355} \cdot \text{1 500,00} \approx \text{1 553,25}}\) |
| 2 | 1 553,25 | \(\mathsf{\text{1,0355} \cdot \text{1 553,25} \approx \text{1 608,39}}\) |
| 3 | 1 608,39 | \(\mathsf{\text{1,0355} \cdot \text{1 608,39} \approx \text{1 664,49}}\) |
| 4 | 1 664,49 | \(\mathsf{\text{1,0355} \cdot \text{1 664,49} \approx \text{1 724,61}}\) |
| 5 | 1 724,61 | \(\mathsf{\text{1,0355} \cdot \text{1 724,61} \approx \text{1 785,84}}\) |
| 6 | 1 785,83 | \(\mathsf{\text{1,0355} \cdot \text{1 785,84} \approx \text{1 849,23}}\) |
| 7 | 1 849,23 | \(\mathsf{\text{1,0355} \cdot \text{1 849,23} \approx \text{1 914,88}}\) |
| 8 | 1 914,88 | \(\mathsf{\text{1,0355} \cdot \text{1 914,88} \approx \text{1 982,86}}\) |
| 9 | 1 982,86 | \(\mathsf{\text{1,0355} \cdot \text{1 982,86} \approx \text{2 053,25}}\) |
| 10 | 2 053,25 | \(\mathsf{\text{1,0355} \cdot \text{2 053,25} \approx \text{2 126,14}}\) |
| Vuosi | Tilin saldo (€) | Korko (€) | Uusi saldo (€) |
|---|---|---|---|
| 1 | 1 500,00 | \(\mathsf{\text{0,0355} \cdot \text{1 500,00} = \text{53,25}}\) | \(\mathsf{\text{1 500,00} + \text{53,25} = \text{1 553,25}}\) |
| 2 | 1 553,25 | \(\mathsf{\text{0,0355} \cdot \text{1 553,25} = \text{55,140...} \approx \text{55,14}}\) | \(\mathsf{\text{1 553,25} + \text{55,14} = \text{1 608,39}}\) |
| 3 | 1 608,39 | \(\mathsf{\text{0,0355} \cdot \text{1 608,39} = \text{57,097...} \approx \text{57,10}}\) | \(\mathsf{\text{1 608,39} + \text{57,10} = \text{1 664,49}}\) |
| 4 | 1 664,49 | \(\mathsf{\text{0,0355} \cdot \text{1 664,49} = \text{59,124...} \approx \text{59,12}}\) | \(\mathsf{\text{1 664,49} + \text{59,12} = \text{1 724,61}}\) |
| 5 | 1 724,61 | \(\mathsf{\text{0,0355} \cdot \text{1 724,61} = \text{61,223...} \approx \text{61,23}}\) | \(\mathsf{\text{1 724,61} + \text{61,23} = \text{1 785,83}}\) |
| 6 | 1 785,83 | \(\mathsf{\text{0,0355} \cdot \text{1 785,84} = \text{63,396...} \approx \text{63,40}}\) | \(\mathsf{\text{1 785,83} + \text{63,40} = \text{1 849,23}}\) |
| 7 | 1 849,23 | \(\mathsf{\text{0,0355} \cdot \text{1 849,23} = \text{65,647...} \approx \text{65,65}}\) | \(\mathsf{\text{1 849,23} + \text{65,65} = \text{1 914,88}}\) |
| 8 | 1 914,88 | \(\mathsf{\text{0,0355} \cdot \text{1 914,88} = \text{67,978...} \approx \text{67,98}}\) | \(\mathsf{\text{1 914,88} + \text{67,98} = \text{1 982,86}}\) |
| 9 | 1 982,86 | \(\mathsf{\text{0,0355} \cdot \text{1 982,86} = \text{70,391...} \approx \text{70,39}}\) | \(\mathsf{\text{1 982,86} + \text{70,39} = \text{2 053,25}}\) |
| 10 | 2 053,25 | \(\mathsf{\text{0,0355} \cdot \text{2 053,25} = \text{72,890...} \approx \text{72,89}}\) | \(\mathsf{\text{2 053,25} + \text{72,89} = \text{2 126,14}}\) |
Potenssi on lyhyempi tapa merkitä toistuvaa kertolaskua. Potensseja opiskellaan 8. luokalla myöhemmin, mutta nyt riittää tieto, että esimerkiksi kertolasku \(\mathsf{2 \cdot 2 \cdot 2 \cdot 2 = 2^4}\).
Prosenttikerroin:
\(\mathsf{\text{100 %} + \text{3,55 %} = \text{103,55 %} = \text{1,0355}}\)
Saldo kymmenen vuoden kuluttua:
\(\mathsf{\text{1 500 €} \cdot \text{1,0355}^{10} = \text{2 126,14 €}}\)
Vastaus: Tilin saldo on 10 vuoden kuluttua 2 126,14 euroa.
Lainat
Jos olet ostamassa asuntoa, ja lainaat rahaa pankista, joudut maksamaan lainasta korkoa. Korko sidotaan usein euromaiden yhteiseen viitekorkoon Euriboriin, joten sen suuruus riippuu ajankohdasta. 2000-luvulla Euribor on vaihdellut 0 % ja 5 % välillä. Vuodesta 2016 vuoteen 2021 Euribor oli (alle) 0 prosenttia, mutta Venäjän hyökkäyssodan vuoksi asetettujen talouspakotteiden myötä monet hinnat lähtivät nousuun ja Euribor noustettiin noin 4 prosenttiin. Lainasta maksetaan koron lisäksi muitakin maksuja, jolloin yleensä ilmoitetaan vain ns. todellinen vuosikorko. Korko lasketaan jäljellä olevata lainan määrästä vuosittain.
Esimerkki: Helinä ostaa asunnon, ja saa pankista siihen 230 000 euron asuntolainan. Lainan todellinen vuosikorko on 5,2 %. Kuinka paljon Helinä maksaa korkoja ensimmäisen vuoden aikana?
Prosenttikerroin: \(\mathsf{\text{5,2 %} = \text{0,052}}\)
Korko: \(\mathsf{\text{0,052} \cdot \text{230 000 €} = \text{11 960 €}}\)
Vastaus: Korkoja maksetaan ensimmäisenä vuonna 11 960 euroa.
Jotta lainan suuruus pienenisi ajan kuluessa, niin korkojen maksamisen lisäksi lainaa lyhennetään kuukausittain tietyllä summalla.
Esimerkki: Kuinka paljon Helinä maksaa korkoa toisena vuonna, kun korkojen maksun lisäksi Helinä lyhentää lainaa 12 000 euroa ensimmäisen vuoden aikana?
Lyhennys: \(\mathsf{\text{230 000 €} - \text{12 000 €} = \text{218 000 €}}\)
Korko: \(\mathsf{\text{0,052} \cdot \text{218 000 €} = \text{11 336 €}}\)
Vastaus: Korkoja maksetaan toisena vuonna 11 336 euroa.
Pikavipit
Pikavippi eli pienlaina on nopeasti myönnettävä vakuudeton laina. Takaisinmaksuajat ovat pikavipeissä yleensä lyhyitä, joten pienetkin lisäkulut (korot ja käsittelymaksut) saavat todellisen vuosikoron näyttämään todella suurilta muihin lainoihin verrattuna. Todellisella vuosikorolla tarkoitetaan korkoa, joka vuoden takaisinmaksuajalla tulisi maksaa. Todellisen vuosikoron voi yksinkertaistetusti laskea seuraavan kaavan avulla:
\(\textsf{Todellinen vuosikorko} = \mathsf{\dfrac{Kulut}{Laina} \cdot \dfrac{365}{Takaisinmaksuaika}}\)
\(\textsf{Tod. vuosikorko} = \mathsf{\dfrac{Kulut}{Laina} \cdot \dfrac{365}{Takaisinmaksuaika}}\)
Esimerkki: Ernolla tulee yllättävä vika autoon, ja huoltoa varten Ernon tarvitsee ottaa 600 euron pikavippi. Takaisin Erno pystyy vipin maksamaan palkkapäivänään kolmen viikon (21 päivän) kuluttua. Korko- ja käsittelykuluja vipistä muodostuu 50 euroa.
Todellinen vuosikorko:
\(\mathsf{\dfrac{\text{50 €}}{\text{600 €}} \cdot \dfrac{365}{21} = \text{1,428}... \approx \text{143 %}}\)
Vastaus: Todellinen vuosikorko on 143 prosenttia.
9. Pitoisuudet
Elintarvikkeiden, kemikaalien ja monien muiden tuotteiden sisältämät ainesosat voidaan ilmoittaa esimerkiksi prosentteina, promilleina, miljoonasosina (ppm - parts per million) riippuen tarkasteltavan määrän suuruudesta suhteessa kokonaismäärään. Vertailtavana yksikkönä käytetään yleisesti massan (mg, g, kg) tai tilavuuden (litra, m3) yksiköitä riippuen tarkasteltavien aineiden tai seoksen olomuodosta (kiinteä, neste, kaasu).
Massa- ja tilavuusprosentit
Prosenttiosuuksia voidaan pitoisuuden mittaamiseen, jos niiden määrät on esitetty käyttäen samaa yksikköä. Nesteiden ja kaasujen tapauksessa käytetään usein tilavuuden yksiköitä kun taas kiinteistä aineista on taas helpompi mitata massaa. Erilaisissa seoksissa ja liuoksissa käytetään tilanteeseen sopivaa yksikköä riippuen mittausvälineistä.
Esimerkiksi elintarvikkeiden tuoteselosteissa ilmoitetaan erilaisten ravintoarvojen massa grammoina. Alla on kuva ruisleivän ravintosisällöstä.

Kuten huomataan, ravintosisältö on annettu suhteessa 100 g ruisleipää. Tätä samaa menetelmää käytetään myös muissa elintarvikkeissa, jolloin vertailu eri tuotteiden välillä on helpompaa. Käytännössä 100 g on valittu siksi, että siihen verrattuna ravintoarvojen määrät ovat suoraan niiden massaprosentteja. Rasvaa ruisleivässä on siis 1,7 %, hiilihydraatteja 41 % ja niin edelleen.
Esimerkki: 300 grammaan vettä liuotetaan 30 grammaa sokeria. Mikä on liuoksen sokeripitoisuus?
Liuosta yhteensä: \(\mathsf{\text{300 g} + \text{30 g} = \text{330 g}}\)
Sokeripitoisuus: \(\mathsf{\dfrac{\text{30 g}}{\text{330 g}} = \text{0,0909}... \approx \text{9,1 %}}\)
Vastaus: Liuoksen sokeripitoisuus on 9,1 prosenttia.
Esimerkki: Viinipullossa on 0,75 litraa viiniä, ja viinin alkoholipitoisuus on 14,5 tilavuusprosenttia. Kuinka paljon puhdasta alkoholia on pullollisessa viiniä? Anna vastaus desilitroina.
Prosenttikerroin:
\(\mathsf{\text{14,5 %} = \text{0,145}}\)
Viiniä (dl):
\(\mathsf{\text{0,75 l} = \text{7,5 dl}}\)
Puhdasta alkoholia:
\(\mathsf{\text{0,145} \cdot \text{7,5 dl} = \text{1,0875 dl} \approx \text{1,1 dl}}\)
Vastaus: Pullollisessa viiniä on 1,1 desilitraa puhdasta alkoholia.
Esimerkki: 100 millilitraa (ml) 10-prosenttista vetyperoksidiliuosta pitäisi laimentaa siten, että liuos olisi 3-prosenttista. Kuinka paljon vettä liuokseen tulee lisätä?
Vetyperoksidia (ml):
\(\mathsf{\text{0,1} \cdot \text{100 ml} = \text{10 ml}}\)
3-prosenttista liuosta:
\(\mathsf{\dfrac{\text{10 ml}}{\text{0,03}} = \text{333,33... ml}}\)
Vettä pitää lisätä alkuperäiseen liuokseen:
\(\begin{align}\mathsf{\text{333,33... ml} - \text{100 ml}} &= \mathsf{\text{233,33... ml}}\\ &\approx \textsf{233 ml}\end{align}\)
Vastaus: Vettä tulee lisätä 233 millilitraa.
Promille
Pienissä pitoisuuksissa prosentti (eli sadasosa) ei ole mielekäs yksikkö, vaan tällöin voidaan käyttää promillea eli tuhannesosaa. Promilleilla laskeminen tapahtuu samaan tapaan kuin prosenteilla, mutta nyt promilleluku muutetaankin promillekertoimeksi jakamalla luvulla 1000. Vastaavasti promillekertoimesta saadaan promilleluku kertomalla luvulla 1000. Promillen yksikkönä käyteään ‰-merkkiä.
Esimerkki: Veren alkoholipitoisuus ilmoitetaan promilleina. Rattijuopumuksen raja on 0,5 promillea. Kuinka paljon alkoholia saa veressä olla, jos 100 kiloisella kuljettajalla on noin 7 kg verta? Ilmoita vastaus grammoina.
Promillekerroin: \(\mathsf{\text{0,5 ‰} = \text{0,0005}}\)
Veren määrä (g): \(\mathsf{\text{7 kg} = \text{7 000 g}}\)
Alkoholia veressä: \(\mathsf{\text{0,0005} \cdot \text{7 000 g} = \text{3,5 g}}\)
Vastaus: Veressä saa olla enintään 3,5 grammaa alkoholia.
Erilaiset jalometallit merkitään pitoisuusleimoin, jonka muoto kertoo metallin ja luku sen pitoisuuden promilleina. Alla on esitetty Suomessa hyväksytyt pitoisuudet ja leimojen pohjamuodot.

Lähde: TUKES (viitattu: 21.5.2024)
Esimerkki: Kultakoru valmistetaan sekoittamalla 13,1 grammaan kultaa 9,2 grammaa hopeaa.
a) Kuinka monta promillea kultakorussa kultaa?
Korun kokonaispaino: \(\mathsf{\text{13,1 g} + \text{9,2 g} = \text{22,3 g}}\)
Kullan osuus: \(\mathsf{\dfrac{\text{13,1 g}}{\text{22,3 g}} = \text{0,5874...} \approx \text{587 ‰}}\)
Vastaus: Kultakorussa on 587 promillea kultaa.
b) Millainen pitoisuusleima koruun laitetaan?

Karaatti
Karaattia käytetään sekä massa- että pitoisuusyksikkönä.
Karaatti massayksikkönä
Jalokivien massa mitattaessa käytetään karaattia, jonka lyhenne on ka. Yksi karaatti on 200 mg eli 0,2 grammaa.
Esimerkki: Maailman suurin luonnontimantti Cullinan oli ennen leikkaamistaan 3 106 karaatin painoinen. Ilmoita timantin massa grammoina.
\(\mathsf{\text{3 106} \cdot \text{0,2 g} = \text{621,2 g}}\)
Vastaus: Timantti painoi 621,2 grammaa.
Karaatti pitoisuusyksikkönä
Karaatti on myös vanha jalometallien pitoisuuden yksikkö, jota ei enää virallisesti käytetä Suomessa pitoisuuden yksikkönä, mutta ulkomailla se on yleisesti käytetty. Yksi karaatti on \(\mathsf{\dfrac{1}{24}}\) esimerkiksi korun massasta, eli puhdas jalometalli (yleensä kulta) on siis 24 karaattia. Pitoisuusyksikkönä karaatin lyhenne on K.
Esimerkki: Ulkomailta tuodussa kultakorussa on leima 18K eli sen kultapitoisuus on 18 karaattia. Kuinka monta promillea korussa on kultaa, ja mikä olisi sen pitoisuusleima?
\(\mathsf{\dfrac{18}{24} = \text{0,75} = \text{750 ‰}}\)
Vastaus: Kultakorussa on 750 promillea kultaa, ja sen leima olisi  .
.