MA8 Jakso 1: Yhtälönratkaisu
1. Kertausta
7. luokalla opittiin perusteita kirjainlaskennasta, kun tutustuttiin muuttujiin, muuttujalausekkeisiin sekä niiden sieventämiseen ja arvon laskemiseen. 8. luokalla näitä taitoja kehitetään edelleen tutustumalla yhtälönratkaisuun, polynomeihin sekä potenssilausekkeisiin.
Termi
Termi muodostuu luvun ja muuttujan tulosta. Termiä merkittäessä kertomerkki jätetään merkitsemättä. Lukua kutsutaan termin kertoimeksi ja muuttujaa (sekä myöhemmin sen astetta) muuttujaosaksi.
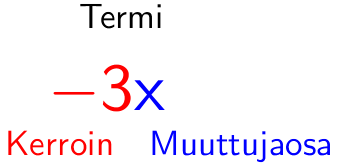
Jos kerroin on 1 tai -1, ykköstä ei merkitä näkyviin: \(\mathsf{1a = a}\) ja \(\mathsf{-1x = -x}\).
Lisäksi termiä, jossa ei ole muuttujaosaa, kutsutaan vakiotermiksi. Vakiotermi on siis pelkkä luku.
Muuttujalauseke
Muuttujalauseke on lauseke, jossa esiintyy vähintään yksi muuttuja. Esimerkiksi matematiikassa ja fysiikassa esiintyy kaikenlaisia muuttujalausekkeita, joiden avulla mallinnetaan esimerkiksi luonnon ilmiöitä, kappaileiden kokoa, muotoa tai prosenttilaskennan laskusääntöjä.
Muuttujalausekkeen arvon laskeminen on yksi peruskoulumatematiikan tärkeimmistä opittavista taidoista. Muuttujalausekkeen arvo voidaan laskea, jos tunnetaan muuttujan arvo. Muuttujan arvo sijoitetaan lausekkeeseen muuttujan paikalle, jonka jälkeen lausekkeen arvo voidaan laskea.
Esimerkki: Laske lausekkeen \(\mathsf{3x + 4}\) arvo, kun muuttuja saa arvon \(\mathsf{x = 2}\).
\(\begin{align}\mathsf{3x + 4} &= \mathsf{3\cdot 2 + 4}\\ &= \mathsf{6 + 4}\\ &= \mathsf{10}\end{align}\)
Sijoitettaessa negatiivista lukua muuttujan paikalle, tulee luku kirjoittaa sulkeiden sisään.
Esimerkki: Laske edellisen esimerkin lausekkeen arvo muuttujan arvolla \(\mathsf{x=-1}\).
\(\begin{align}\mathsf{3x + 4} &= \mathsf{3\cdot (-1) + 4}\\ &= \mathsf{-3 + 4}\\ &= \mathsf{1}\end{align}\)
Lausekkeen sieventäminen
Peräkkäisistä termeistä koostuvaa muuttujalauseketta kutsutaan polynomiksi. Tämä käsite tarkentuu myöhemmässä jaksossa 8. luokalla. 7. luokalla opittiin sieventämään muuttujalausekkeessa olevia samanmuotoisia termejä (yhteen- ja vähennyslasku). Samanmuotoisilla termeillä on täsmälleen sama muuttujaosa.
Esimerkki: Sievennä.
a) \(\mathsf{{\color{red}4}x + {\color{red}3}x = {\color{red}7}x}\)
Termit ovat samanmuotoisia, joten voidaan sieventää laskemalla kertoimet yhteen.
b) \(\mathsf{5a - 3b}\)
Termit eivät ole samanmuotoisia, joten ei voida sieventää.
c) \(\mathsf{{\color{red}5}a - {\color{red}3}a = {\color{red}2}a}\)
Termit ovat samanmuotoisia, joten voidaan sieventää vähentämällä kertoimet toisistaan.
d) \(\mathsf{{\color{red}4a}{\color{blue}\;-\; 3b}{\color{red}\;-\;a}{\color{blue}\;+\;7b} = {\color{red}3a}{\color{blue}\;+\;4b}}\)
Keskenään samanmuotoiset termit voidaan sieventää.
Lisäksi opittiin sieventämään lausekkeita, joissa termiin kohdistuu kerto- tai jakolasku.
Esimerkki: Sievennä.
a) \(\mathsf{{\color{red}4} \cdot {\color{red}5}x = {\color{red}20}x}\)
b) \(\mathsf{{\color{red}-3}x \cdot ({\color{red}-5}) = {\color{red}15}x}\)
c) \(\mathsf{\dfrac{{\color{red}42}x}{\color{red}7} = {\color{red}6}x}\)
d) \(\mathsf{\dfrac{{\color{red}-32}x}{{\color{red}8}x} = {\color{red}-4}}\)
Lausekkeen kertominen luvulla
Kertolaskun yhteydessä 7. luokalla opittiin ns. osittelulakiin perustuva päässälaskumenetelmä, jonka avulla voitiin laskea helposti kertolasku, jonka toisena tekijänä on suuri luku. Suuri luku pilkotaan osiin (ykkösiin, kymmeniin, satoihin, ...), kerrotaan osia, ja yhdistetään uudet osat takaisin yhdeksi luvuksi.
Esimerkki: Laske.
\(\begin{align}\mathsf{9 \cdot 183} &= \mathsf{9 \cdot (100 + 80 + 3)}\\ &= \mathsf{900 + 720 + 27}\\ &= \mathsf{1647}\end{align}\)
Tätä menetelmää käytetään myös tilanteessa, jossa muuttujalauseketta kerrotaan luvulla (tai termillä).
Esimerkki: Sievennä.
\(\mathsf{4 \cdot (2a + b - 8)} = \mathsf{8a + 4b - 32}\)
Kertolasku kohdistuu siis kaikkiin muuttujalausekkeen termeihin.
Lisätietoa: Yhteisen tekijän etsiminen
Edellä opittua lausekkeen kertomista luvulla voidaan soveltaa myös toiseen suuntaan, ja selvittää lausekkeessa esiintyvien termien yhteiset osat. Tätä voidaan hyödyntää tietynlaisissa yhtälöiden ratkaisemisessa sekä murtolausekkeiden sieventämisessä.
Esimerkki: Jaa muuttujalauseke tekijöihin.
\(\mathsf{5x + 10 = {\color{red}5} \cdot x + {\color{red}5} \cdot 2 = {\color{red}5} \cdot (x + 2)}\)
Jos edellä sievennettyä lauseketta esimerkiksi jaetaan, voidaan nyt jakolasku kohdistaa yhteiseen tekijään.
Esimerkki: Sievennä.
\(\mathsf{\dfrac{5x+10}{5} = \dfrac{5 \cdot (x+2)}{5} = x+2}\)
Tällä tavoin vältetään yleinen virhe, jossa supistus kohdistuu vain yhteen lausekkeen termiin.
Murtoyhtälöllä tarkoitetaan tilannetta, jossa yhtälössä esiintyy murtolukumerkintä. 7. luokalta muistetaan, että murtoluku kuvaa jakolaskua, joten käytännössä ollaan siis tekemisissä jakolaskun kanssa. Kerrataan aluksi hieman murtolukujen laskutoimituksia, ja tutustutaan erilaisiin merkintävaihtoehtoihin.
Murtoluvut
Murtoluku koostuu osoittajasta sekä nimittäjästä, ja niitä erottavasta murtoviivasta. Murtoluku on jakolasku, jonka laskeminen on tarkoituksella jätetty kesken, jotta voidaan kuvata selkeästi kokonaisen osia ilman desimaalilukuja. Laskemalla murtoluvun osoittama jakolasku eli murtoluvun arvo, saadaan murtoluku muutettua desimaaliluvuksi.
Esimerkki: Muunna murtoluku desimaaliluvuksi.
a) \(\mathsf{\dfrac{2}{5} = 0,\!4}\)
b) \(\mathsf{\dfrac{1}{3} = 0,\!333...}\)
Murtolukua voidaan muokata supistamalla ja laventamalla. Supistamisessa murtoluvun osoittaja sekä nimittäjä jaetaan samalla luvulla, ja laventamisessa molemmat puolestaan kerrotaan samalla luvulla. Supistaminen ja laventaminen eivät muuta murtoluvun arvoa.
Esimerkki: Laske.
a) \(\mathsf{{\dfrac{6}{8}}^{(2} = \dfrac{3}{4}}\)
b) \(\mathsf{\rule{0pt}{1.2em}^{3)}\!\dfrac{5}{6} = \dfrac{15}{18}}\)
Murtolukuja voidaan laskea yhteen ja vähentää toisistaan. Tällöin murtolukujen tulee olla samannimisiä, eli niillä on oltava sama nimittäjä. Jos nimittäjät eivät ole samat, ne voidaan laventaa samannimisiksi.
Esimerkki: Laske.
a) \(\mathsf{\dfrac{2}{7} + \dfrac{3}{7} = \dfrac{5}{7}}\)
b) \(\mathsf{\rule{0pt}{1.2em}^{2)}\!\dfrac{3}{5} + \dfrac{1}{10} = \dfrac{6}{10} + \dfrac{1}{10} = \dfrac{7}{10}}\)
Murtolukua voidaan kertoa ja jakaa kokonaisluvulla tai toisella murtoluvulla. Murtolukujen kertolaskussa osoittajat kerrotaan keskenään, ja nimittäjät kerrotaan keskenään.
Esimerkki: Laske.
a) \(\mathsf{4 \cdot \dfrac{3}{7} = \dfrac{4 \cdot 3}{7} = \dfrac{12}{7} = 1\dfrac{5}{7}}\)
b) \(\mathsf{\dfrac{2}{3} \cdot \dfrac{5}{6} = \dfrac{2 \cdot 5}{3 \cdot 6} = {\dfrac{10}{18}}^{(2} = \dfrac{5}{9}}\)
Murtolukujen jakolasku kannattaa muuttaa aina ensin kertolaskuksi kääntämällä jakaja käänteisluvukseen.
Esimerkki: Laske.
\(\mathsf{\dfrac{3}{4} : \dfrac{1}{8} = \dfrac{3}{4} \cdot \dfrac{8}{1} = \dfrac{3 \cdot 8}{4 \cdot 1} = \dfrac{24}{4} = 6}\)
Tällä tavoin voidaan kuvata myös murtoluvun jakamista kokonaisluvulla, jolloin osoittajan jakamisen sijaan voidaankin tarvittaessa kertoa nimittäjää.
Esimerkki: Laske.
\(\mathsf{\dfrac{1}{2} : 3 = \dfrac{1}{2} \cdot \dfrac{1}{3} = \dfrac{1 \cdot 1}{2 \cdot 3} = \dfrac{1}{6}}\)
2. Yhtälö
Yhtälöllä tarkoitetaan matematiikan ongelmaa, jossa kaksi lauseketta on merkitty yhtä suuriksi. Esimerkiksi yhtälössä \(\mathsf{2x-4 = -x + 5}\) on lausekkeet \(\mathsf{2x-4}\) ja \(\mathsf{-x+5}\) merkitty yhtä suuriksi. Merkintä tarkoittaa sitä, että lausekkeet saavat saman arvon jollakin muuttujan \(\mathsf{x}\) arvolla. Yhtälön ratkaisu , eli muuttujan \(\mathsf{x}\) arvo saadaan selvitettyä ratkaisemalla yhtälö. Tästä lisää luvussa "Yhtälön ratkaiseminen".
Yhtälön ratkaisun tutkiminen
Jos halutaan testata, onko jokin tietty muuttujan arvo yhtälön ratkaisu, voidaan muuttujan arvo sijoittaa yhtälön molempiin lausekkeisiin, ja tutkia lausekkeiden arvojen yhtäsuuruutta.
Esimerkki: Onko \(\mathsf{x=2}\) yhtälön \(\mathsf{2x-4 = -x + 5}\) ratkaisu?
\(\begin{align}\mathsf{2x-4} &= \mathsf{-x + 5}\\\mathsf{2 \cdot 2 - 4} &= \mathsf{-2+5}\\\mathsf{0} &= \mathsf{3}\end{align}\)
Väite on epätosi.
Vastaus: \(\mathsf{x=2}\) ei ole yhtälön ratkaisu.
Yhtälöön liittyviä käsitteitä ja merkintöjä
Yhtäsuuruusmerkki jakaa yhtälön kahteen osaan, joita kutsutaan vasemmaksi puoleksi ja oikeaksi puoleksi .
\(\begin{align}\mathsf{3x+1} &= \mathsf{-x+6}\\ \textsf{vasen puoli} &\phantom{=} \textsf{oikea puoli}\end{align}\)
Kuten yhtälön ratkaisua tutkittaessa aikaisemmassa esimerkissä havaittiin, yhtälöä muokattaessa muokattu yhtälö kirjoitetaan aina edellisen alapuolelle siten, että yhtäsuuruusmerkit tulevat allekkain. Tällöin yhtälön vasen ja oikea puoli ovat helpommin erotettavissa toisistaan.
Lisää yhtälöistä
Yhtälöitä käytetään matemaattisissa aineissa (matematiikkan, fysiikka, kemia, tietotekniikka) paljon. 8. luokalla opiskellaan ns. 1. asteen yhtälöitä, vaillinaisia 2. asteen yhtälöitä sekä verrantoja, ja 9. luokalla laajennetaan 8. luokan tietämystä 2. asteen yhtälöihin, yhtälöpareihin sekä epäyhtälöihin. Matematiikassa ja fysiikassa tutustutaan erilaisiin säännönmukaisuuksiin ja luonnonlakeihin laskukaavojen (yhtälöiden) avulla, joita voidaan muokata käyttötarkoitukseen sopiviksi yhtälöratkaisun menetelmin. Esimerkiksi keskinopeuden laskukaavaa kuvataan yhtälöllä
\(\mathsf{\text{nopeus} = \dfrac{\text{matka}}{\text{aika}}}\),
josta voidaan johtaa yhtälönratkaisun avulla laskukaavat matkalle ja ajalle:
\(\mathsf{\text{matka} = \text{nopeus} \cdot \text{aika}}\)
\(\mathsf{\text{aika} = \dfrac{\text{matka}}{\text{nopeus}}}\)
Peruskoulun jälkeen on lukiossa ja eri korkeakouluissa mahdollista opiskella lineaarisia yhtälöryhmiä, joita käytetään esim. GPS-paikannuksessa ja tietokonegrafiikassa tai differentiaali- sekä osittaisdifferentiaaliyhtälöitä, joita käytetään monimutkaisemmissa matemaattisissa malleissa, kuten sään ennustuksessa.
3. Yhtälönratkaisu
Yhtänlönratkaisussa on tavoitteena selvittää muuttujan \(\mathsf{x}\) arvo, jolla yhtälö on tosi, eli yhtäsuuruus pätee. Jokin yhtälön ratkaisuista voidaa saada päättelemällä, mutta varmin, helpoin ja oikea tapa on ratkaista yhtälö vaiheittain lisäämällä, vähentämällä, kertomalla tai jakamalla yhtälöä puolittain sopivilla luvuilla. Vaiheittain etenemällä saadaan ratkaisulle perustelu ja löydetään kaikki mahdolliset ratkaisut. Tämän vuoksi päättely ei enää käy kuin saadun ratkaisun järkevyyden tarkasteluun.
Yhtälöä voidaan siis muokata suorittamalla sama laskutoimitus yhtälön molemmille puolille. Laskutoimitus on tärkeätä suorittaa molemmille puolille yhtälöä, koska tällöin oikean ja vasemman puolen yhtäsuuruus pysyy voimassa. Yhtälön ratkaiseminen loppuu, kun muuttuja \(\mathsf{x}\) on saatu jäämään yksin vain yhtälön toiselle puolelle.
Laskutoimitus, joka yhtälön molemmille puolille kullakin rivillä tehdään, merkitään rivin loppuun kahden pystyviivan \(\|\) oikealle puolelle. Laskutoimitusten muokkaama uusi yhtälö kirjoitetaan edellisen alapuolelle siten, että yhtäsuuruusmerkit ovat samassa pysysuorassa linjassa.
Yhtälön ratkaiseminen jakamalla puolittain
Tarkastellaan yhtälöä
\(\mathsf{3x = 24}\)
Nyt siis muuttujaa \(\mathsf{x}\) on kerrottu luvulla 3, vastaukseksi on saatu 24. Tästä on toki helppoa päätellä, että muuttujan x on oltava 8, koska \(\mathsf{3 \cdot 8 = 24}\). Ratkaisu saadaan käänteisesti jakolaskun avulla: \(\mathsf{24:3=8}\), koska jakolasku on kertolaskun käänteinen laskutoimitus. Yhtälöratkaisun menetelmien avulla ratkaisu näyttäisi seuraavalta.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{3x} &= \mathsf{24} \quad &&\mathsf{\|\color{red}:3}\\ \mathsf{x} &= \mathsf{8}\end{align}\)
1. rivillä on siis alkuperäinen yhtälö \(\mathsf{3x = 24}\). Pystyviivojen \(\|\) jälkeen on laskutoimitus, joka yhtälön molemmille puolille tehdään.
2. rivillä nähdään laskutoimituksen tulos. Vasemmalla on siis laskettu \(\mathsf{3x\;{\color{red}: 3} = x}\) ja oikealla \(\mathsf{24\;{\color{red}: 3}=8}\). Näin yhtälö on saatu ratkaistua, ja ratkaisuksi on saatu edellä päätelty \(\mathsf{x = 8}\).
Yhtälön ratkaiseminen lisäämällä tai vähentämällä puolittain
Tarkastellaan yhtälöä
\(\mathsf{x - 4 = 5}\)
Nyt muuttujasta x on vähennetty luku 4. Käytetään apuna jälleen käänteistä laskutoimitusta, joka vähennyslaskulle on tietenkin yhteenlasku. Lisäämällä yhtälön molemmille puolille luku 4, saadaan yhtälön vasemmalla puolella -4 häviämään nollaksi. Yhtälönratkaisun merkinnöin saadaan siis
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{x - 4} &= \mathsf{5}\quad &&\mathsf{\|\color{red}+4}\\ \mathsf{x} &= \mathsf{9}\end{align}\)
Vasemmalla laskettiin nyt \(\mathsf{x - 4 {\color{red}\;+\;4} = x}\) ja oikealla \(\mathsf{5{\color{red}\;+\;4} = 9}\). Ratkaisuksi saatiin siis \(\mathsf{x = 9}\), joka voidaan tarkistaa sijoittamalla ratkaisu alkuperäiseen yhtälöön. \(\mathsf{x-4 = 9-4 = 5}\).
Myös termejä, joissa esiintyy muuttuja x voidaan lisätä ja vähentää puolittain. Tarkastellaan yhtälöä
\(\mathsf{3x = x + 8}\)
Nyt molemmilla puolilla yhtälöä on termi, jossa esiintyy muuttuja x. Koska tavoitteena oli saada muuttuja x jäämään yksin vain yhtälön toiselle puolelle, poistetaan x toiselta puolelta. Tehdään se tällä kertaa yhtälön oikealta puolelta.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{3x} &= \mathsf{x + 8}\quad &&\mathsf{\|\color{red}-x}\\\mathsf{2x} &= \mathsf{8}&&\mathsf{\|:2}\\ \mathsf{x} &= \mathsf{4}\end{align}\)
Vasemmalla saadaan siis \(\mathsf{3x{\color{red}\;-\;x} = 2x}\) ja oikealla \(\mathsf{x + 8 {\color{red}-x} = 8}\). Muuttujalle x jää vielä kerroin, joka saadaan poistettua aiemmin opitulla jakolaskulla puolittain.
Yhtälönratkaisu kokonaisuutena
Yhtälönratkaisusta opittiin edellä selvittämään kolme hieman erilaista tilannetta. Näitä kolmea menetelmää apuna käyttäen voidaan ratkaista mikä tahansa 1. asteen yhtälö enintään kolmella vaiheella. Alla olevassa vuokaaviossa on esitetty algoritmi yhtälönratkaisuun.
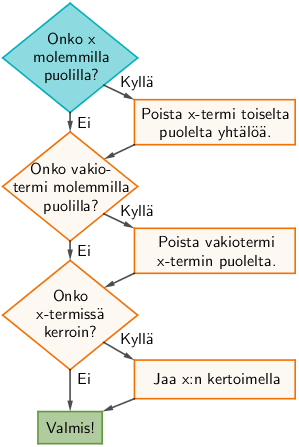
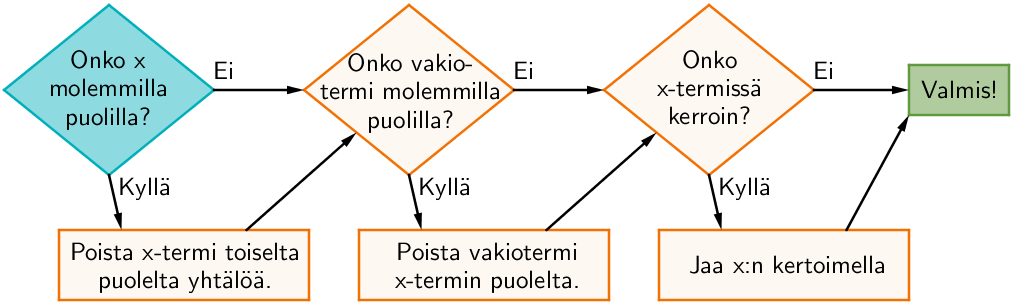
Esimerkki: Ratkaise yhtälö \(\mathsf{2x-4 = -x + 5}\) algoritmin avulla.
Onko x molemmilla puolilla? Kyllä on, joten poistetaan x-termi toiselta puolelta yhtälöä.
\(\begin{align}\mathsf{2x-4} &= \mathsf{-x+5}&&\mathsf{\|+x}\\\mathsf{3x-4} &= \mathsf{5}\end{align}\)
Onko vakiotermi molemmilla puolilla? Kyllä on, joten poistetaan vakiotermi x-termin puolelta.
\(\begin{align}\mathsf{3x-4} &= \mathsf{5}&&\mathsf{\|+4}\\\mathsf{3x} &= \mathsf{9}\end{align}\)
Onko x-termissä kerroin? Kyllä on, joten jaetaan x:n kertoimella.
\(\begin{align}\mathsf{3x} &= \mathsf{9}&&\mathsf{\|:3}\\\mathsf{x} &= \mathsf{3}\end{align}\)
Valmis!
Yhtälönratkaisun vastaus voidaan tarkistaa laskemalla erikseen vasemman ja oikean puolen lausekkeiden arvot. Niiden pitäisi olla siis yhtä suuret.
Esimerkki: Onko \(\mathsf{x=3}\) yhtälön \(\mathsf{2x-4=-x+5}\) ratkaisu?
Vasen: \(\mathsf{2x-4 = 2 \cdot 3 - 4 = 6 - 4 = 2}\)
Oikea: \(\mathsf{-x+5 = -3+5 = 2}\)
Vastaus: x = 3 on yhtälön ratkaisu.
Yhtälönratkaisun esivalmistelut
Nyt kun yhtälönratkaisun perusperiaatteet ovat hallussa, kannattaa käyttää muutama ajatus yhtälön tarkastelulle ennen varsinaisten ratkaisutoimien aloittamista. Joskus yhtälön lausekkeita joudutaan sieventämään ennen puolittaisten laskutoimitusten (sukset) tekemistä.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{2x+3x} &= \mathsf{3+7}\\\mathsf{5x} &= \mathsf{10} && \mathsf{\|:5}\\\mathsf{x} &= \mathsf{2}\end{align}\)
Yllä olevassa yhtälössä sievennettiin ensin vasemmalla \(\mathsf{2x+3x=5x}\) ja oikealla \(\mathsf{3+7=10}\). Tämän jälkeen päästiin vasta suorittamaan puolittainen jakolasku.
Mielenkiintoisempi tilanne syntyy, kun toisessa (tai molemmissa) lausekkeissa on luvulla kerrottu lauseketta. Tällaiseen tilanteeseen on olemassa kaksi tapaa lähestyä ongelmaa
Esimerkki: Ratkaise yhtälö.
Tapa 1: Poistetaan sulut sieventämällä, ja jatketaan yhtälönratkaisua normaalisti.
\(\begin{align}\mathsf{2 \cdot (x+3)} &= \mathsf{18}\\\mathsf{2x+6} &= \mathsf{18} && \mathsf{\|-6}\\\mathsf{2x} &= \mathsf{12} &&\mathsf{\|:2}\\\mathsf{x} &= \mathsf{6}\end{align}\)
Tapa 2: Jaetaan sulkeiden kertoimella, jos oikealla on sopivasti jaollinen luku.
\(\begin{align}\mathsf{2 \cdot (x+3)} &= \mathsf{18} &&\mathsf{\|:2}\\\mathsf{x+3} &= \mathsf{9} && \mathsf{\|-3}\\\mathsf{x} &= \mathsf{6}\end{align}\)
4. Murtoyhtälöt
Murtoyhtälöllä tarkoitetaan tilannetta, jossa yhtälössä esiintyy murtolukumerkintä.
Yksinkertaiset murtoyhtälöt
Yksinkertaisimmillaan muuttujalla \(\mathsf{x}\) on jakaja, josta pyritään pääsemään eroon. Jakolaskun vastakkainen laskutoimitus on kertolasku, joten kertomalla \(\mathsf{x}\):n jakajalla , päästää jakajasta eroon.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{\dfrac{x}{4}} &= \mathsf{3} &&\|\cdot \mathsf{4}\\\mathsf{x} &= \mathsf{12}\end{align}\)
Yhtälön vasemmalla puolella olevaa lauseketta voidaan merkitä myös siten, että muuttujalla \(\mathsf{x}\) on murtolukukerroin.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{\dfrac{1}{4}x} &= \mathsf{3} &&\|\cdot \mathsf{4}\\\mathsf{x} &= \mathsf{12}\end{align}\)
Hieman monimutkaisemmat murtoyhtälöt
Yhtälössä voi olla tuttuun tapaan myös vakiotermejä, jolloin vakiotermit kannattaa poistaa x:n puolelta kuten aiemmin on opittu.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{\dfrac{x}{2} + 3} &= \mathsf{2} &&\mathsf{\|-3}\\\mathsf{\dfrac{x}{2}} &= \mathsf{-1} &&\|\cdot \mathsf{2}\\\mathsf{x} &= \mathsf{-2}\end{align}\)
Muuttujalla \(\mathsf{x}\) voi olla myös kerroin, jolloin kertolaskun lisäksi pitää myös jakaa \(\mathsf{x}\):n kertoimella.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{\dfrac{3x}{4}} &= \mathsf{6} &&\|\cdot \mathsf{4}\\\mathsf{3x} &= \mathsf{24} && \mathsf{\|:3}\\\mathsf{x} &= \mathsf{8}\end{align}\)
Joissain tilanteissa voi hyödyllistä laskea jakolasku ennen kertolaskua, jolloin laskettavat luvut pysyvät pienempinä.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{\dfrac{3x}{4}} &= \mathsf{6} && \mathsf{\|:3}\\\mathsf{\dfrac{x}{4}} &= \mathsf{2} && \|\cdot \mathsf{4}\\\mathsf{x} &= \mathsf{8}\end{align}\)
Vielä hieman monimutkaisemmat murtoyhtälöt
Murtolausekkeen osoittajassa voi olla myös kokonainen lauseke, jolloin jakajalla kertominen kannattaa suorittaa ehdottomasti ensin.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{\dfrac{-x+5}{3}} &= \mathsf{-1} &&\|\cdot \mathsf{3}\\\mathsf{-x+5} &= \mathsf{-3} && \mathsf{\|-5}\\\mathsf{-x} &= \mathsf{-8} && \mathsf{\|:(-1)}\\\mathsf{x} &= \mathsf{8}\end{align}\)
Aivan hurjaksi tilanne menee, kun murtolausekkeita on molemmilla puolilla yhtälöä. Aluksi kannattaa kertoa sopivalla luvulla, jolla saadaan molemmat jakajat pois. Muista kertoa tarvittaessa ylijäävällä osalla osoittajaa.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{\dfrac{2x-4}{3}} &= \mathsf{\dfrac{-x+7}{6}} && \mathsf{\|\cdot 6}\\ \mathsf{4x-8} &= \mathsf{-x+7} && \mathsf{\|+x}\\\mathsf{5x-8} &= \mathsf{7} && \mathsf{\|+8}\\ \mathsf{5x} &= \mathsf{15} && \mathsf{\|:5}\\ \mathsf{x} &= \mathsf{3}\end{align}\)
Myöhemmin 8. luokalla opitaan verrannon käsite ja ratkaisemaan verrantoyhtälöitä, jolloin näihinkin tilanteisiin saadaan vaihtoehtoisia ratkaisumenetelmiä.
5. Lisätietoa: Suoran yhtälö
Suora voidaan määritellä myös muuttujalausekkeen avulla. Lähtöajatuksena on muodostaa y-koordinaatille laskukaava, missä muuttujana on x-koordinaatti. Tällä tavoin luodaan x- ja y-koordinaatin välille riippuvuus eli sääntö, jolla x- ja y-koordinaatit riippuvat toisistaan. Suora on riippuvuuksista yksinkertaisin, mutta käyttämällä kerto- ja yhteenlaskun lisäksi muitakin matematiikassa opittavia työkaluja saadaan aikaan monimutkaisempia riippuvuuksia.
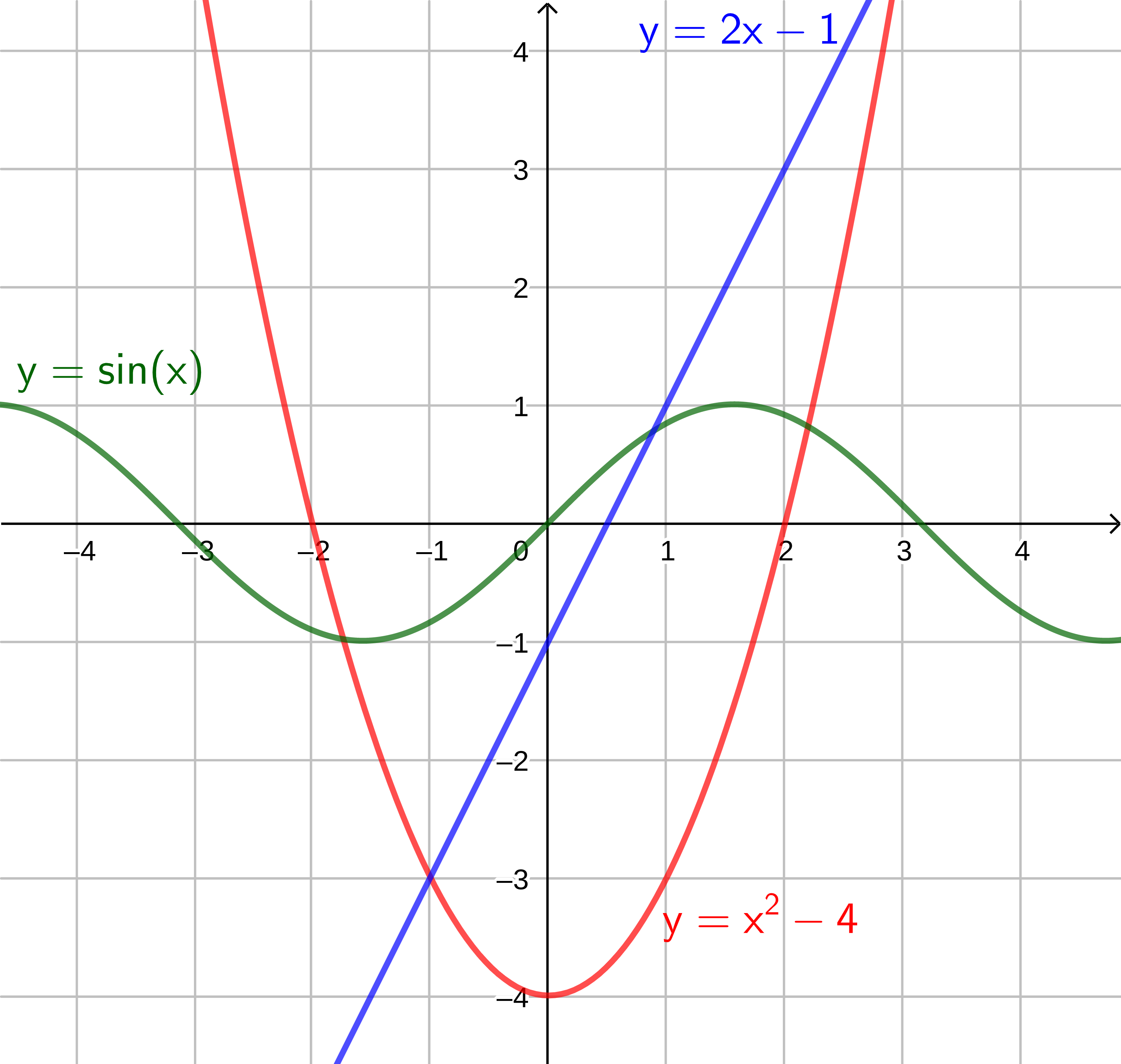
Suoran yhtälössä on aina kaksi termiä. Ensimmäisen termin kerrointa kutsutaan suoran kulmakertoimeksi. Toista termiä kutsutaan tuttuun tapaan vakiotermiksi . Molemmilla käsitteillä on tärkeä ja havainnollinen rooli suoran sijainnissa koordinaatistossa.
Esimerkki: Määritä suoran yhtälöstä kulmakerroin ja vakiotermi.
a) \(\mathsf{y = 2x+1}\)
Kulmakerroin: 2
Vakiotermi: 1
b) \(\mathsf{y = -5x+5}\)
Kulmakerroin: -5
Vakiotermi: 5
c) \(\mathsf{y = 3x-2}\)
Kulmakerroin: 3
Vakiotermi: -2
Erityisesti muistetaan kertoimet 1 ja 0
Esimerkki: Määritä suoran yhtälöstä kulmakerroin ja vakiotermi.
a) \(\mathsf{y = x+2}\)
Kulmakerroin: 1
Vakiotermi: 2
b) \(\mathsf{y = -3}\)
Kulmakerroin: 0
Vakiotermi: -3
c) \(\mathsf{y = 4x}\)
Kulmakerroin: 4
Vakiotermi: 0
Kulmakerroin
Kulmakerroin kertoo suoran kaltevuuden. Mittayksikkönä voidaan ajatella käytettävän y-akselin suuntaista muutosta, kun x-koordinaatin suuruus kasvaa yhdellä. Toisin sanoen, piirretään suoralle (mihin tahansa) piste, liikutaan yhden verran oikealle, ja lasketaan kuinka paljon tulee siirtyä ylös (tai alas), jotta päästään takaisin suoralle. Alla oleva kuva havainnollistaa kulmakertoimen \(\mathsf{k}\) määrittämistä suoran kuvaajasta.
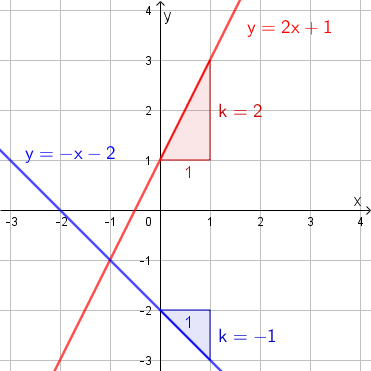
Tarkalleen ottaen kulmakerroin määritellään y-akselin suuntaisen siirtymän \(\mathsf{\Delta y}\) ja x-akselin suuntaisen siirtymän \(\mathsf{\Delta x}\) osamääränä. Alla olevasta kuvassa on esimerkkinä kulmakertoimen \(\textsf{k}\) määrittäminen tällä tavoin.
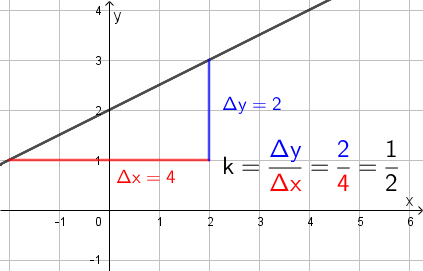
Jos kulmakerroin on positiivinen, sanotaan että suora on nouseva. Vastaavasti kulmakertoimen ollessa negatiivinen, suora on laskeva.
Vakiotermi
Vakiotermi kertoo suoran ja y-akselin leikkauskohdan. Toisin sanoen vakiotermi on suoran ja y-akselin leikkauspisteen y-koordinaatti, sillä x-koordinaattihan on tällöin aina 0. Vakiotermiä muuttamalla voidaan siis muuttaa suoran sijaintia y-akselin suunnassa. Alla olevassa kuvassa on esitetty yhdensuuntaisia suoria, joiden vakiotermi on eri.