MA7 Jakso 5: Geometria 2

1. Kertausta

Desimaaliluvut

Desimaaliluvulla kuvataan niitä lukuja, joissa on kokonaisten lisäksi myös kokonaisen osia. Desimaaliosa erotetaan kokonaisosasta pilkulla. Paikkojen nimeäminen perustuu samaan logiikkaan kuin kokonaisillakin luvuilla.

Pilkun vasemmalla puolella on siis kokonaisosa, joka koostuu tuttuun tapaan ykkösistä, kymmenistä, sadoista, tuhansista jne.

Pilkun oikealla puolella desimaaliosa alkaa vasemmalta luettuna kymmenesosista, sadasosista, tuhannesosista jne.

Desimaaliluvut lukusuoralla

Lukusuoralla desimaalilukuja käytetään kokonaisten välissä kuvaamaan kymmenesosien, sadasosien, jne. avulla kokonaisten osia. Desimaalilukuja on loputtomasti, jokaisen desimaaliluvun välistä voidaan aina löytää uusi desimaaliluku.

https://jannevenhoedu.github.io/ma7/j1/t/ma7j1_teoria_lukusuoraR_pieni.ggb

https://jannevenhoedu.github.io/ma7/j1/t/ma7j1_teoria_lukusuoraR.ggb

Desimaalilukujen summa ja erotus päässälaskuna

Myös päässälaskiessa kannattaa ennen laskemista lisätä nollia desimaaliosan loppuun, mikäli luvuissa on eri määrä desimaaleja. Tämä helpottaa hahmottamaan paremmin lukujen desimaaliosan suuruutta ja suhdetta toisiinsa.

Esimerkki: Laske.

$\textsf{7,5 + 2,34 = 7,50 + 2,34 = 9,84}$

Toinen päässälaskua helpottava ajatusmalli on laskea kokonaisosa ja desimaaliosa erikseen, ja yhdistää ne sitten lopuksi. Esimerkiksi

Esimerkki: Laske.

$\begin{align}&\mathsf{{\color{red}27}{,}{\color{blue}54} + {\color{red}51}{,}{\color{blue}62}}\\&=\mathsf{{\color{red}27 + 51} + {\color{blue}0{,}54 + 0{,}62}}\\&=\mathsf{{\color{red}78} + {\color{red}1}{,}{\color{blue}16}}\\&=\mathsf{{\color{red}79}{,}{\color{blue}16}}\end{align}$

Desimaalilukujen kertominen ja jakaminen kymmenen moninkerroilla

Kymmenen moninkerroilla kerrottaessa desimaaliluvussa pilkku siirtyy oikealle nollien osoittaman määrän verran.

Esimerkki: Laske.

a) $\mathsf{3{,}14 \cdot 10 = 31{,}4}$

b) $\mathsf{3{,}14 \cdot 100 = 314}$

c) $\mathsf{3{,}14 \cdot 1000 = 3140}$

Jos numerot, joiden yli pilkkua voidaan siirtää, loppuvat kesken, lisätään tarvittaessa luvun loppuun nollia.

Jaettaessa kymmenen moninkerroilla pilkku siirtyy puolestaan vasemmalle. Tällöin saattaa ilmetä tarve lisätä nollia luvun eteen pilkun siirtämisen mahdollistamiseksi.

Esimerkki: Laske.

a) 78,3 : 10 = 7,83

b) 78,3 : 100 = 0,783

c) 78,3 : 1000 = 0,0783

Desimaalilukujen kerto- ja jakolasku päässälaskuna

Tietyissä tapauksissa desimaalilukujen kerto- ja jakolaskuja voidaan laskea helposti myös päässälaskuna. Tällöin tulee olla lähinnä tarkkana pilkun paikasta vastauksessa, johon voidaan käyttää allekkainlaskusta opittua taktiikkaa. Kertolasku voidaan laskea aluksi välittämättä pilkusta ja lopuksi lisätä pilkku oikeaan paikkaan. Oikea paikka määräytyy lähtöarvojen desimaalien lukumäärän mukaan.

Esimerkki: Laske.

a) $\mathsf{6 \cdot \text{0,3} = \text{1,8}}$

b) $\mathsf{2 \cdot \text{0,3} = \text{0,6}}$

c) $\mathsf{\text{0,6} \cdot \text{0,3} = \text{0,18}}$

d) $\mathsf{\text{0,2} \cdot \text{0,3} = \text{0,06}}$

Jakolaskussa voidaan käyttää samaa taktiikkaa kuin allekkainlaskun tapauksessa. Jos jakajassa on desimaaliluku, jakolaskua (murtolukua) kannattaa laventaa siten, että jakajana on kokonaisluku. Tämän avulla voidaan hahmottaa jakolaskua paremmin ja pilkku tulee varmemmin oikeaan paikkaan.

Esimerkki: Laske.

a) $\mathsf{\rule{0pt}{1.5em}^{10)}\!\dfrac{12}{\text{0,3}} = \dfrac{120}{3} = 40}$

b) $\mathsf{\rule{0pt}{1.5em}^{10)}\!\dfrac{\text{4,2}}{\text{0,6}} = \dfrac{42}{6} = 7}$

c) $\mathsf{\rule{0pt}{1.5em}^{10)}\!\dfrac{\text{0,24}}{\text{0,2}} = \dfrac{\text{2,4}}{2} = \text{1,2}}$

d) $\mathsf{\rule{0pt}{1.5em}^{100)}\!\dfrac{1}{\text{0,05}} = \dfrac{100}{5} = 20}$

2. Pituusyksiköt

Pituuden perusyksikkö on metri, ja se lyhennetään pienellä $\textsf{m}$-kirjaimella. Pienempiä ja suurempia pituusyksiköitä saadaan kertomalla tai jakamalla luvulla 10, ja käyttämällä määrättyjä etuliitteitä, kuten milli-, sentti- tai kilo. Perusyksikköä metri lähimmät pituusyksiköt lyhenteineen on esitetty alla olevassa taulukossa.

km	hm	dam	m	dm	cm	mm
kilometri	hehtometri	dekametri	metri	desimetri	senttimetri	millimetri
1000 m	100 m	10 m	1 m	0,1 m	0,01 m	0,001 m

Kun pituus muutetaan pienempään yksikköön, lukua kerrotaan 10:llä, eli pilkku siirtyy oikealle.

Esimerkki: Muunna suluissa annettuun yksikköön.

a) $\textsf{8 cm (mm)}$

$\textsf{8 cm = 80 mm}$

Pilkku siirtyy oikealle yhden numeron yli.

b) $\textsf{6,4 m (cm)}$

$\textsf{6,4 m = 640 cm}$

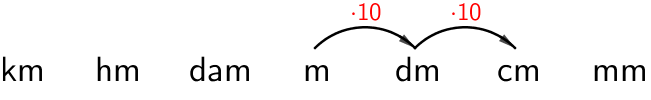
Pilkku siirtyy oikealle kahden numeron yli.

c) $\textsf{0,2 km (m)}$

$\textsf{0,2 km = 200 m}$

Pilkku siirtyy oikealle kolmen numeron yli.

Kun muutetaan suurempaan yksikköön, luku vastaavasti jaetaan 10:llä, eli pilkku siirtyy vasemmalle.

Esimerkki: Muuta suluissa annettuun yksikköön.

a) $\textsf{2500 dm (m)}$

$\textsf{2500 dm = 250 m}$

Pilkku siirtyy vasemalle yhden numeron yli.

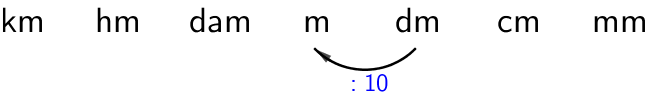
b) $\textsf{140 dam (km)}$

$\textsf{140 dam = 1,4 km}$

Pilkku siirtyy vasemmalle kahden numeron yli.

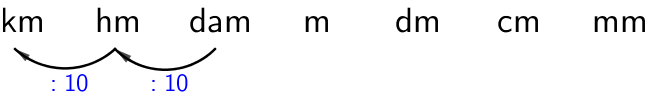
c) $\textsf{952 mm (m)}$

$\textsf{952 mm = 0,952 m}$

Pilkku siirtyy vasemmalle kolmen numeron yli.

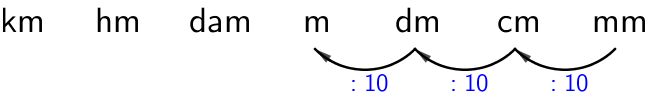
3. Pinta-alayksiköt

Pinta-ala kuvaa kaksiulotteisen kuvion suuruutta. Egyptiläisestä Rhindin papyruksesta (n. 1650 eaa.) on löytynyt varhaisimpia pinta-alojen laskemiseen tarkoitettuja esimerkkejä. Egyptissä faarao oli antanut ihmisille viljelysmaata, ja määrännyt siitä veron, joten peltojen pinta-ala piti pystyä laskemaan.

Pinta-alan perusyksikkö on neliömetri, ja se lyhennetään $\mathsf{m^2}$-merkinnällä ($\mathsf{1\:m \cdot 1\:m = 1\:m^2}$). Pienempiä ja suurempia pinta-alayksiköitä saadaan kertomalla tai jakamalla luvulla 100, ja käyttämällä määrättyjä etuliitteitä, kuten pituusyksiköissä. Poikkeuksena on neliöhehtometri eli hehtaari sekä neliödekametri eli aari. Tärkeimmät pinta-alayksiköt lyhenteineen on esitetty alla olevassa taulukossa.

km²	ha	a	m²	dm²	cm²	mm²
neliökilometri	hehtaari	aari	neliömetri	neliödesimetri	neliösenttimetri	neliömillimetri
1 000 000 m²	10 000 m²	100 m²	1 m²	0,01 m²	0,0001 m²	0,000001 m²

Kun siirrytään pienempiin yksiköihin, niin jokaisessa vaiheessa kerrotaan luvulla 100.

Esimerkki: Muuta suluissa annettuun yksikköön.

a) $\mathsf{\textsf{8 cm}^2\;(\textsf{mm}^2})$

$\mathsf{\textsf{8 cm}^2 = \textsf{800 mm}^2}$

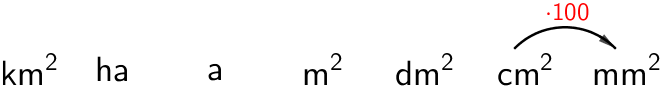
Pilkku siirtyy oikealle kahden numeron yli.

b) $\mathsf{\textsf{6,4 m}^2\;(\textsf{cm}^2})$

$\mathsf{\textsf{6,4 m}^2 = \textsf{64 000 cm}^2}$

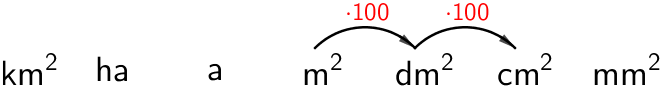
Pilkku siirtyy oikealle neljän numeron yli.

c) $\mathsf{\textsf{0,2 km}^2\;(\textsf{m}^2})$

$\mathsf{\textsf{0,2 km}^2 = \textsf{20 000 m}^2}$

Pilkku siirtyy oikealle kuuden numeron yli.

Kun muutetaan suurempaan yksikköön, luku vastaavasti jaetaan 100:lla.

Esimerkki: Muuta suluissa annettuun yksikköön.

a) $\mathsf{\textsf{2500 dm}^2\;(\textsf{m}^2})$

$\mathsf{\textsf{2500 dm}^2 = \textsf{25 m}^2}$

Pilkku siirtyy vasemmalle kahden numeron yli.

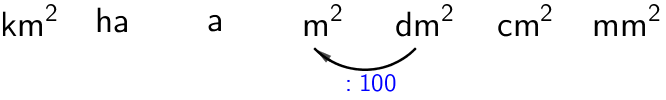
b) $\mathsf{\textsf{1 400 a}\;(\textsf{km}^2})$

$\mathsf{\textsf{1 400 a} = \textsf{0,14 km}^2}$

Pilkku siirtyy vasemmlle neljän numeron yli.

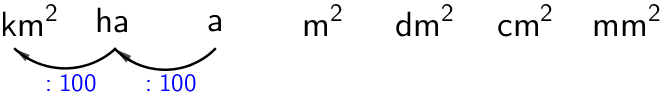
c) $\mathsf{\textsf{2 195 000 mm}^2\;(\textsf{m}^2})$

$\mathsf{\textsf{2 195 000 mm}^2 = \textsf{2,195 m}^2}$

Pilkku siirtyy vasemmalle kuuden numeron yli.

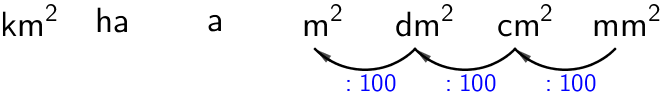
4. Pyöristäminen

Geometriassa mitataan erilaisia suureita kuten viivojen pituuksia ja kulmien suuruuksia. Näillä mittaustuloksilla voidaan laskea esimerkiksi piirejä ja pinta-aloja. Mittaustuloksiin liittyy kuitenkin aina mittalaitteesta (ja joskus mittaajastakin) johtuvaa epätarkkuutta. Esimerkiksi tavallisella viivottimella ei voida mitata kuin millimetrien tarkkuudella. Tämän vuoksi mittaustuloksilla suoritettujen laskujen vastaukset tulee pyöristää eli muuttaa mittaustulosten (lähtöarvojen) kanssa yhtä epätarkkaan muotoon.

Desimaalilukujen tapauksessa pyöristäminen tulee ajankohtaiseksi paljon useammin kuin kokonaislukujen tapauksessa. Usein esimerkiksi jakolasku ei mene tasan, ja vastauksena voi olla päättymätön desimaaliluku, joka pitäisi pyöristää järkevään tarkkuuteen. Pyöristyksessä tarkkuus voidaan esittää kolmella eri tavalla:

Numeron paikan perusteella
Desimaalien lukumäärän perusteella (summa ja erotus)
Merkitsevien numeroiden perusteella (tulo ja osamäärä)

Valittu tarkkuus määritellään sen mukaan, mistä laskutoimituksesta tai mittalaitteesta pyöristettävä desimaaliluku on peräisin. Epätarkin lähtöarvo määrittää pyöristyksen tarkkuuden.

Pyöristäminen numeron paikan perusteella

Esimerkiksi sadasosien tarkkuuteen pyöristettäessä pyöristysraja tulee siis sadasosia kuvaavan numeron perään.

Esimerkki: Pyöristä luku 593,1415

a) satojen tarkkuuteen

$ \mathsf{\text{5} {\color{red}|}\text{93,1415} \approx \text{600}} $

b) kymmenien tarkkuuteen

$ \mathsf{\text{59} {\color{red}|}\text{3,1415} \approx \text{590}} $

c) kokonaisten tarkkuuteen

$ \mathsf{\text{593,} {\color{red}|}\text{1415} \approx \text{593}} $

d) sadasosien tarkkuuteen

$ \mathsf{\text{593,14} {\color{red}|}\text{15} \approx \text{593,14}} $

e) tuhannesosien tarkkuuteen.

$ \mathsf{\text{593,141} {\color{red}|}\text{5} \approx \text{593,142}} $

Pyöristyksen tapahtuessa desimaaliosan puolella, pyöristettyjä desimaaleja ei korvata nollilla, vaan viimeinen numero (oikealla) kuvaa pyöristetyn luvun tarkkuuttaa, ja sen on oltava sama kuin haluttu tarkkuus.

Pyöristäminen desimaalien lukumäärän perusteella

Yhteen- ja vähennyslaskujen vastausta pyöristettäessä tutkitaan lähtöarvojen desimaalien lukumäärää, jonka perusteella vastauskin pyöristetään. Tästä tarkemmin alempana. Tarkkuuden ilmoittamiseen desimaalien lukumäärä on selkeä.

Esimerkki: Pyöristä luku 9,5297

a) kolmen desimaalin tarkkuuteen

$ \mathsf{\text{9,529}{\color{red}|}\text{7} \approx \text{9,530}} $

b) yhden desimaalin tarkkuuteen

$ \mathsf{\text{9,5}{\color{red}|}\text{297} \approx \text{9,5}} $

c) kokonaisten tarkkuuteen

$ \mathsf{\text{9,}{\color{red}|}\text{5297} \approx \text{10}} $

Jos lasketaan yhteen esimerkiksi kahta metreinä ilmoitettua pituutta, joista toinen on mitattu kahden desimaalin (senttimetrin) tarkkuudella ja toinen kolmen desimaalin (millimetrin) tarkkuudella, joudutaan valitsemaan lähtöarvoista epätarkempi (kaksi desimaalia), jonka mukaisesti vastaus pyöristetään.

Esimerkki: Laske pituuksien 14,39 m ja 3,217 m summa.

$ \mathsf{\text{14,39 m} + \text{3,217 m} = \text{17,607 m} \approx \text{17,61 m}} $

Pyöristäminen merkitsevien numeroiden perusteella

Esimerkiksi kerto- ja jakolaskujen vastauksia pyöristettäessä tutkitaan lähtöarvojen merkitsevien numeroiden määrää. Tutustutaan ensin merkitseviin numeroihin, jotta niiden avulla pyöristäminen onnistuu.

Merkitsevät numerot

Kokonaislukujen tapauksessa merkitseviä numeroita ovat kaikki numerot, paitsi luvun lopussa olevat nollat.

Esimerkki: Montako merkitsevää numeroa on luvussa

a) 204 912

Luvun lopussa ei ole nollia, joten kaikki numerot ovat merkitseviä.

Vastaus: Luvussa 204 912 on kuusi merkitsevää numeroa.

b) 842 500

Luvun lopussa on kaksi nollaa, joten vain numerot 8, 4, 2 ja 5 ovat merkitseviä.

Vastaus: Luvussa 842 500 on neljä merkitsevää numeroa.

Desimaalilukujen tapauksessa merkitseviä numeroita ovat kaikki numerot, paitsi luvun alussa olevat nollat.

Esimerkki: Montako merkitsevää numeroa on luvussa

a) 3,1415

Luvun alussa ei ole nollia, joten kaikki numerot ovat merkitseviä.

Vastaus: Luvussa 3,1415 on viisi merkitsevää numeroa.

b) 0,00280

Luvun alussa on kolme nollaa, joten vain numerot 2, 8 ja 0 ovat merkitseviä.

Vastaus: Luvussa 0,00280 on kolme merkitsevää numeroa.

Pyöristäminen merkitsevien numeroiden tarkkuuteen

Pyöristystarkkuus voidaan antaa siis myös haluttujen merkitsevien numeroiden perusteella.

Esimerkki: Pyöristä luku 1,893

a) yhden merkitsevän numeron tarkkuuteen

$ \mathsf{\text{1,}{\color{red}|}\text{893} \approx \text{2}} $

b) kahden merkitsevän numeron tarkkuuteen

$ \mathsf{\text{1,8}{\color{red}|}\text{93} \approx \text{1,9}} $

c) kolmen merkitsevän numeron tarkkuuteen

$ \mathsf{\text{1,89}{\color{red}|}\text{3} \approx \text{1,89}} $

Mittaustulosten kerto- ja jakolaskun tapauksessa epätarkkuus saattaisi kertaantua liian suureksi, jos sen vastauksen pyöristämiseen käytettäisiin desimaalien tarkkuutta. Tämän vuoksi tulos pyöristetäänkin merkitsevien numeroiden tarkkuudella.

Esimerkki: Laske A4-paperin pinta-ala, kun sen mitat ovat 29,7 cm ja 21 cm.

$ \mathsf{\text{29,7 cm} \cdot \text{21 cm} = \text{623,7 cm}^2 \approx \text{620 cm}^2} $

Vastaus: A4-paperin pinta-ala on 620 cm².

Lähtöarvoista 29,7 oli siis kolmen merkitsevän ja 21 vain kahden merkitsevän numeron tarkkuudella ilmoitettu. Näistä valitaan vastauksen pyöristystarkkuudeksi epätarkempi, eli kaksi merkitsevää numeroa. Jos oltaisiin varmoja, että 21 cm onkin tarkalleen 21,0 cm, niin tällöin vastaus pyöristettäisiin kolmen merkitsevän numeron tarkkuuteen, ja vastaus olisi 624 cm².

5. Monikulmiot

Laajennetaan erilaisten viivojen ja niiden välisten suuntaerojen (kulmien) tarkastelua tasokuviohin. Viivoista (lähinnä janoista) voitiin mitata vain pituus, mutta tasokuvioista voidaan mitata/laskea ympärysmitan (piiri) lisäksi sen pinta-ala.

Tasokuvioista ensimmäisenä tutustutaan monikulmiohin. Tarkastellaan aluksi monikulmioita yleisesti, ja siirrytään sitten tarkemmin yksinkertaisimpiin ja jatkon kannalta hyödyllisempiin monikulmioihin kuten kolmio ja nelikulmio. Seuraavassa jaksossa (Jakso 6) tutustutaan vielä ympyrään, ja opitaan laskemaan pinta-aloja monikulmioille sekä tutkitaan yhdenmuotoisia ja yhteneviä monikulmioita.

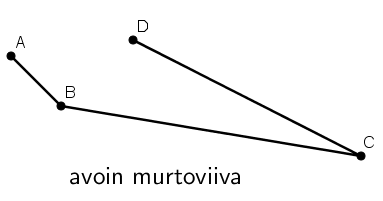
Murtoviiva

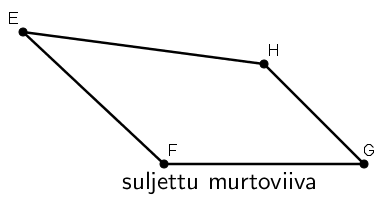
Laitettaessa janoja peräkkäin, muodostuu murtoviiva. Murtoviiva voi olla avoin tai suljettu.

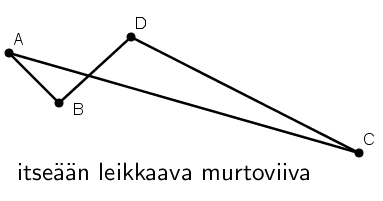
Murtoviiva voi olla itseään leikkaava tai leikkaamaton. Itseään leikkaavan murtoviivan kaksi janaa siis leikkaavat toisiaan.

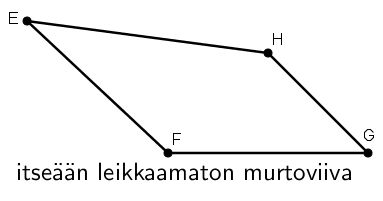
Monikulmion nimeäminen

Itseään leikkaamaton suljettu murtoviiva muodostaa monikulmion. Monikulmio luokitellaan sen kulmien lukumäärän mukaan, kuten kolmio (kolmikulmio), nelikulmio, viisikulmio, kuusikulmio jne. Monikulmio nimetään kärkipisteiden avulla vastapäivään kiertäen.

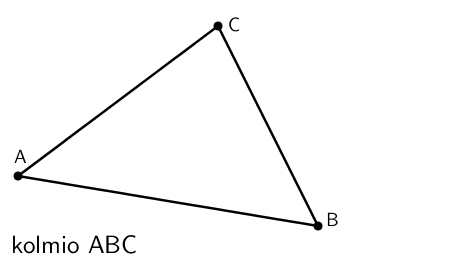
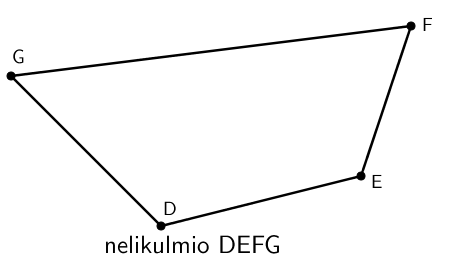
Monikulmion osat

Monikulmion muodostaman murtoviivan janoja kutsutaan sivuiksi. Monikulmiolla on yhtä monta sivua kuin sillä on kulmia. Jos kulmia (ja sivuja) on enemmän kuin kolme, voidaan monikulmiolle piirtää lävistäjä, joka on kahden monikulmion kärkipisteen välinen jana (ei sivu), ja nimensä mukaisesti lävistää monikulmion.

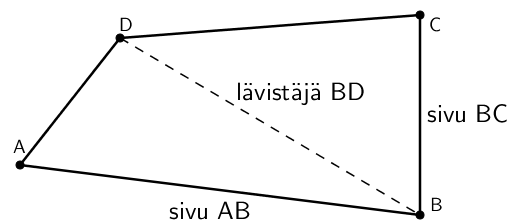
Monikulmion piiri

Monikulmiosta voidaan laskea piiri, joka on sen sivujen summa. Piiriä merkitään muuttujalla $\textsf{p}$.

Esimerkki: Laske nelikulmion piiri.

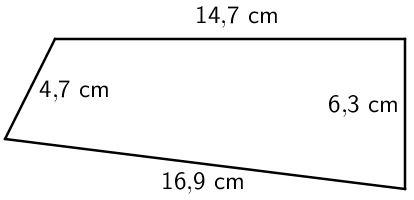
$\begin{align}\textsf{p} &= \textsf{16,9 cm + 6,3 cm + 14,7 cm + 4,7 cm}\\ &= \textsf{42,6 cm}\end{align}$

Monikulmioiden tarkempaa luokittelua käsitellään myöhemmissä luvuissa kolmion ja nelikulmion osalta. Myöhemmissä luvuissa tutustutaan myös säännöllisiin monikulmioihin sekä yhteneviin ja yhdenmuotoisiin monikulmioihin.

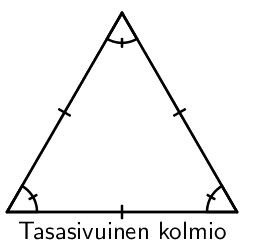
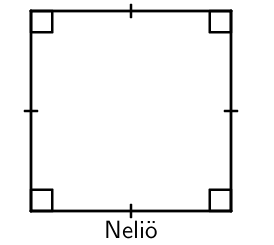
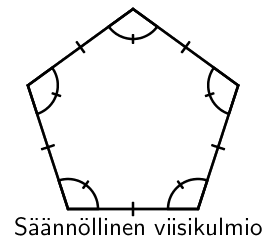
Säännöllinen monikulmio

Säännöllisessä monikulmiossa kaikki sivut ovat yhtä pitkiä, ja kaikki kulmat ovat yhtä suuria.

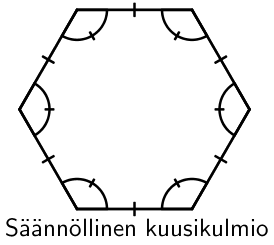
6. Kolmiot

Kolmio on monikulmio, jossa on kolme sivua ja kulmaa. Kolmioita käytetään paljon tietokonegrafiikassa, missä erilaisia pintoja voidaan jakaa kolmioihin laskennan nopetuttamiseksi. Rakennustekniikassa kolmioita käytetään sen lujuuden vuoksi mm. siltojen ja kattorakenteiden rakentamiseen.

Kolmion kulmien summa

Kolmion kulmien summa on aina $\mathsf{180^\circ}$. Kolmion tuntemattoman kulman voi siis laskea, kun tunnetaan kaksi muuta kulmaa.

Esimerkki: Laske kulman $\alpha$ suuruus.

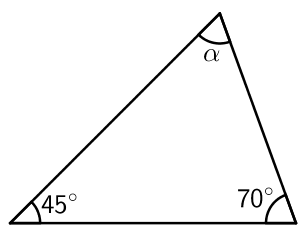
$\mathsf{\alpha = 180^\circ - 45^\circ - 70^\circ = 65^\circ}$

Kolmioiden luokittelu

Kolmiossa on aina siis nimensä mukaisesti kolme kulmaa, ja niistä kaksi on aina teräviä kulmia, eli alle $\mathsf{90^\circ}$. Yksi tapa luokitella kolmioita, on tarkastella kolmannen kulman suuruutta. Teräväkulmaisen kolmion kolmas kulma on terävä, tylppäkulmaisen kolmion kolmas kulma on tylppä, ja suorakulmaisen kolmion kolmas kulma on suora.

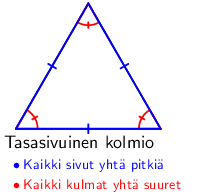
Toinen tapa luokitella kolmioita on tarkastella sivujen pituuksia toisiinsa. Jos kaikki sivut ovat yhtä pitkiä, on kyseessä tasasivuinen kolmio. Tällöin myös kaikki kulmat ovat yhtä suuria.

Jos kaksi sivua ovat yhtä pitkät, kyseessä on tasakylkinen kolmio. Keskenään samanmittaisia sivuja merkitään sivun keskellä olevilla viivoilla.

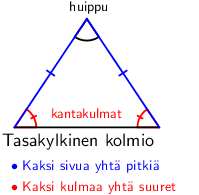
Tasakylkinen kolmio voidaan aina kääntää siten, että samanpituisten sivujen välinen kulma on ylhäällä, jolloin kyseistä kärkipistettä kutsutaan huipuksi. Kaksi muuta kulmaa ovat ns. kantakulmia, ja ovat keskenään yhtä suuria.

Kolmion pinta-ala

Kolmion pinta-alaa laskettaessa tarvitaan suorakulmion tapaan kolmion leveys (kanta) ja korkeus. Leveydeksi eli kannaksi valitaan jokin kolmion sivu, jolloin korkeus on kannan ja kolmannen kärkipisteen välinen kohtisuora etäisyys. Pinta-ala $\textsf{A}$ lasketaan kertomalla kanta $\textsf{a}$ ja korkeus $\textsf{h}$ keskenään, ja jakamalla saatu tulo kahdella. Jos kahdella jakaminen hämmentää, kannattaa tutustua nelikulmioiden pinta-alan laskemiseen, jolloin havaitaan kolmion olevan aina jonkin nelikulmion (suunnikkaan) puolikas.

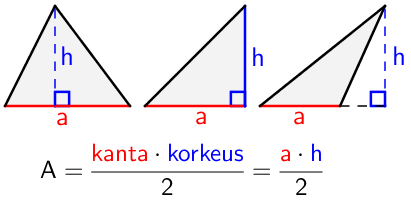
Kun kolmion korkeus merkitään näkyviin, sitä kutsutaan korkeusjanaksi. Suorakulmaisella kolmiolla kannaksi ja korkeudeksi kannattaa valita kohtisuorat sivut. Tylppäkulmaisen kolmion tapauksessa korkeusjana voi tulla kolmion ulkopuolelle, jolloin se on kohtisuorassa kannalle piirretyn jatkeen kanssa.

Esimerkki: Laske kolmion pinta-ala.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_kolmion_pinta-ala_esim.ggb

Kolmion piirtäminen

Kolmion piirtämiseen tarvitaan vähintään kahden kulman suuruus ja yhden sivun pituus tai yksi kulma ja kaksi sivua. Alla olevassa animaatiossa nähdään esimerkki kun tunnetaan kaksi kulmaa ja niiden välisen sivun pituus.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_kolmion_piirto.ggb

7. Nelikulmiot

Nelikulmioita on kaikkialla ihmisen rakentamassa ympäristössä. Varsinkin suorakulmioita ja neliöitä käytetään paljon seinissä, ovissa, ikkunoissa, laatoituksessa, näytöissä, paperiarkeissa jne. Suorakulmioon liittyvät mitat on helposti mitattavissa ja laskettavissa, ja hävikin määrä on usein pienempää kuin esimerkiksi pyöreitä muotoja käytettäessä.

Nelikulmioiden kulmien summa

Nelikulmion kulmien summa on aina $\mathsf{360^\circ}$. Nelikulmion tuntemattoman kulman voi siis laskea, kun tunnetaan kolme muuta kulmaa.

Esimerkki: Laske kulman $\alpha$ suuruus.

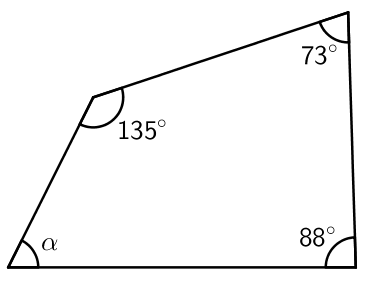
$\mathsf{\alpha = 360^\circ - 135^\circ - 73^\circ - 88^\circ = 63^\circ}$

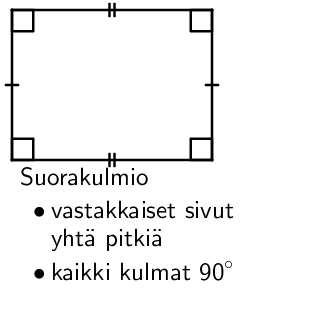
Nelikulmioiden luokittelu

Nelikulmioita luokitellaan kulmien sekä sivujen pituuksien avulla. Käytetyimmät nelikulmiot ovat suorakulmio sekä neliö, ja näiden lisäksi on hyvä tuntea suunnikkaaseen ja puolisuunnikkaaseen liittyvät lainalaisuudet.

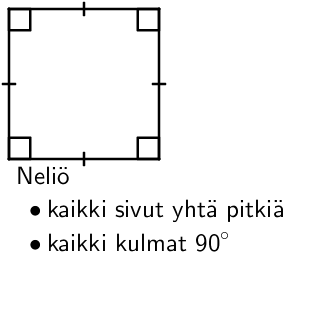
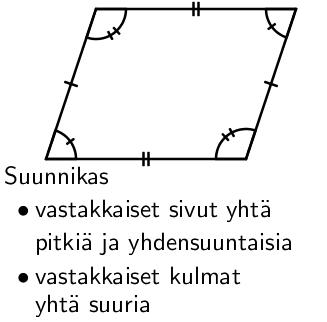
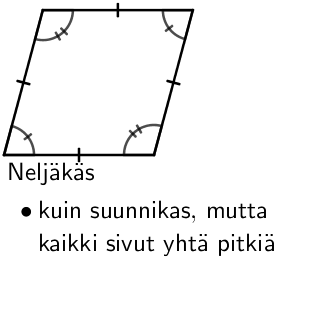
Nelikulmion pinta-ala

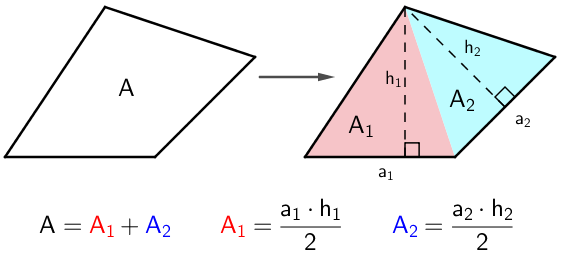
Jos nelikulmiossa ei ole havaittavissa mitään edellä mainittua säännönmukaisuutta, voidaan pinta-alan laskemiseksi jakaa nelikulmio helpommin laskettaviin osiin, joiden pinta-alat voidaan sitten laskea lopuksi yhteen. Nelikulmio voidaan aina jakaa kahdeksi kolmioksi, joiden pinta-ala opittiin edellisessä luvussa laskemaan.

Suorakulmion pinta-ala

Suorakulmion (ja neliön) pinta-ala on kaikkein selkein pinta-ala laskettavaksi. Pinta-alan laskemista varten suorakulmiosta tulee tuntea sen kanta (leveys) ja korkeus. Suorakulmion pinta-ala on kannan ja korkeuden tulo.

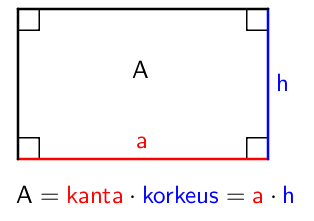
Esimerkki: Laske suorakulmion pinta-ala.

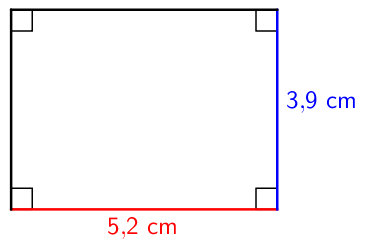
$\mathsf{A = \text{5,2 cm} \cdot \text{3,9 cm} = \text{20,28 cm}^2 \approx \text{20 cm}^2}$

Suunnikkaan pinta-ala

Suunnikkaan pinta-alan laskemista voidaan lähestyä kahdella eri tavalla. Ensiksi, suunnikas voidaan jakaa kahdeksi yhteneväksi (yhtä suureksi) kolmioksi, joiden pinta-alat selvittämällä ja yhteen laskemalla saadaan suunnikkaan pinta-ala. Toisaalta, suunnikas voidaan ajatella suorakulmioksi, jonka yksi kulma on siirtynyt kuvion toiselle puolelle. Tästä voidaan päätellä, että pinta-ala lasketaan kuten vastaavan suorakulmionkin, eli kannan ja korkeuden tulona.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_suunnikkaan_pintaala.ggb

Esimerkki: Laske suunnikkaan pinta-ala.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_suunnikkaan_pinta-ala_esim.ggb

Puolisuunnikkaan pinta-ala

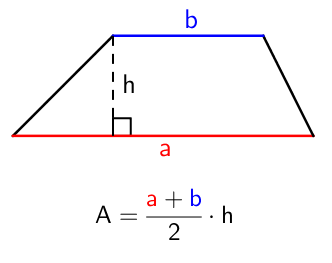
Laskukaavan tarkempi perustelu löytyy luvun lopusta Lisätietoa-otsikon alta.

Suunnikkaan piirtäminen

Suunnikkaan piirtämiseen tarvitaan kahden erisuuntaisen sivun pituus ja niiden välinen kulma. Alla olevassa animaatiossa nähdään esimerkki suunnikkaan piirtämisestä piirtokolmion avulla.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_suunnikkaan_piirto.ggb

Lisätietoa: Puolisuunnikkaan pinta-alan laskukaavan perustelu

Kolmioihin jakamista voidaan käyttää myös puolisuunnikkaan pinta-alan laskukaavan määrittämiseen, kun valitaan kolmioiden kannoiksi puolisuunnikkaan yhdensuuntaiset sivut.

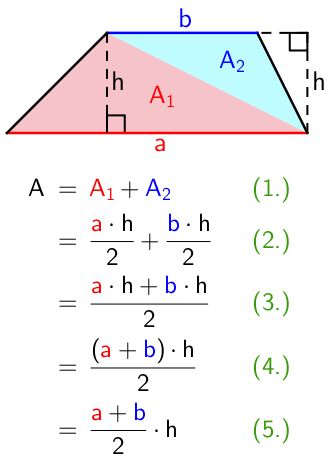
Kaavan sievennys voi 7. luokkalaisesta tuntua vielä hankalalta, koska tarvittavat työkalut opitaan vasta 8. luokalla. Kuvaan on kuitenkin numeroitu sievennyksen vaiheet (1. - 5.), joiden avulla voidaan yrittää selventää, mitä sievennyksessä missäkin vaiheessa tapahtuu.

Puolisuunnikkaan pinta-ala $\mathsf{A}$ on jaettu kahdeksi kolmioksi $\color{red}{\mathsf{A_1}}$ ja $\color{blue}{\mathsf{A_2}}$
Sijoitetaan kolmioiden pinta-alojen laskukaavat lausekkeeseen
$\mathsf{\color{red}{A_1} = \dfrac{\color{red}{a} \cdot h}{2}}$ ja $\mathsf{\color{blue}{A_2} = \dfrac{\color{blue}{b} \cdot h}{2}}$
Lasketaan murtolausekkeet (jakolaskut) yhteen, eli yhdistetään osoittajat, koska murtolausekkeet ovat samannimisiä (sama jakaja).
Koska korkeus $\textsf{h}$ esiintyy molemmissa tuloissa $\mathsf{\color{red}{a} \cdot h}$ ja $\mathsf{\color{blue}{b} \cdot h}$ tekijänä, otetaan se yhteiseksi tekijäksi. 8. luokalla opitaan laskukaava
$\quad\mathsf{a\cdot b + a \cdot c = a \cdot (b + c)}$
Korkeus $\mathsf{h}$ voidaan vielä irroittaa murtolausekkeesta (jakolaskusta).

8. Yhtenevyys

Kaksi kuviota ovat yhteneviä, jos ne ovat täsmälleen saman kokoisia ja muotoisia. Monikulmioiden tapauksessa tämä tarkoittaa, että yhtenevien monikulmioiden vastinkulmat ovat yhtä suuret ja vastinsivut ovat yhtä pitkät. Kuvio on yhtenevä oman peilikuvansa kanssa, ja sen vuoksi peilaus kuuluukin yhtenevyyskuvauksiin.

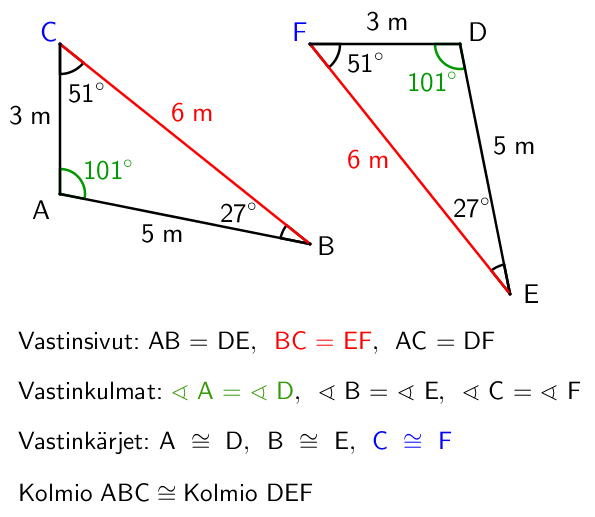
Yhtenevyyttä merkitään esimerkin mukaisesti $\cong$-merkillä. Merkki voidaan lausua "on yhtenevä" tai "vastaa". Yllä olevassa esimerkissä voidaan siis sanoa "Kolmio ABC on yhtenevä kolmion DEF kanssa" tai "Kolmio ABC vastaa kolmiota DEF".

Peilaus suoran suhteen

Kuvio oli siis yhtenevä oman peilikuvansa kanssa. Matematiikassa kuvioiden peilaaminen voidaan tehdä monella tavalla, mutta tutustutaan ensin peilaamiseen suoran suhteen. Peilatessa etsitään jokaiselle kuvion pisteelle vastinpiste peilaussuoran toiselta puolelta, joka on yhtä kaukana suorasta kuin alkuperäinen piste.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_peilaus_suoran_suhteen.ggb

Kuvassa piste $\textsf{A}$ on peilattu suoran $\textsf{l}$ suhteen, ja peilikuvana saatava vastinpiste nimetään lisäämällä heittomerkki alkuperäisen nimen perään, eli peilikuva on $\textsf{A'}$. Heittomerkistä huolimatta, tämä lausutaan "A pilkku".

Tarkastellaan toista esimerkkiä, missä kolmio ABC on peilattu suoran l suhteen, ja tuloksena on saatu kolmio A'B'C'.

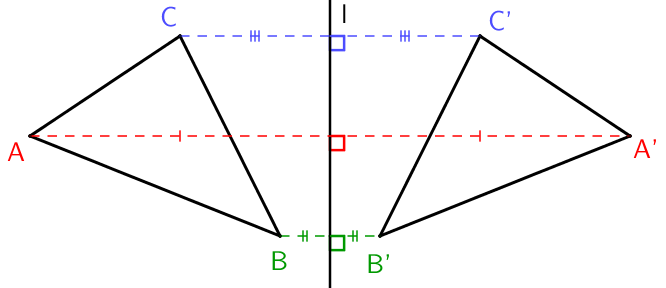
Monikulmioita peilattaessa riittää siis peilata pelkät monikulmion kärkipisteet. Muut pisteet tulevat oikeille paikoilleen, kun monikulmion sivut piirretään uusien kärkipisteiden avulla.

Peilaus pisteen suhteen

Toinen tapa kuvioiden peilaamiseen on peilaus pisteen suhteen. Idea on samakaltainen kuin suorankin suhteen peilatessa, eli etsitään peilikuva yhtä kaukaa peilauspisteestä kuin alkuperäinen piste, mutta vastakkaiselta puolelta. Alla olevasta animaatiosta näet kuinka piste peilataan toisen pisteen suhteen piirtokolmion avulla.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_peilaus_pisteen_suhteen.ggb

Peilikuvan nimeäminen noudattaa samaa käytäntöä kuin suorankin suhteen peilatessa, eli peilikuva nimetään heittomerkkiä ' käyttämällä, ja lausutaan esimerkiksi "A pilkku".

Toisessa esimerkissä tarkastellaan kolmion ABC peilaamista pisteen O suhteen.

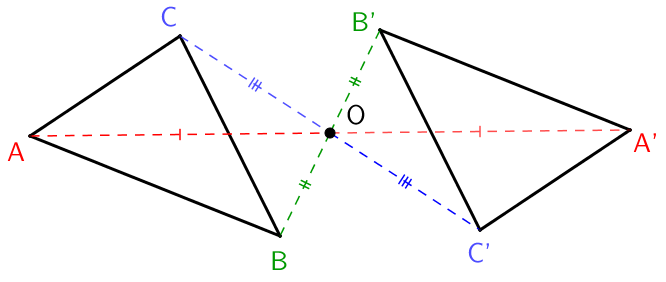
Jälleen peilataan vain kolmion kärkipisteet, ja piirretään kolmio valmiiksi tämän jälkeen. Kolmion minkä tahansa pisteen ja sen vastinpisteen välisen janan keskipiste on aina peilauspisteessä O.

Symmetria

Kaksi kuviota ovat suoran suhteen symmetrisiä, jos niille voidaan piirtää symmetria-akseli siten, että se jakaa kuvion kahteen yhtenevään kuvioon, jotka ovat toistensa peilikuvia kyseisen symmetria-akselin suhteen. Symmetria-akseleita voi olla yksi tai useampia.

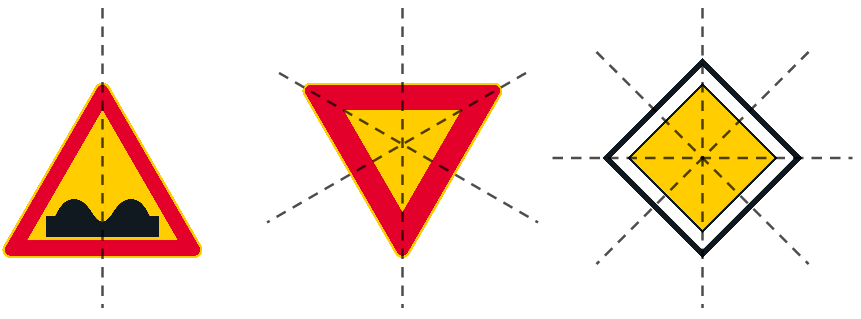
Kaksi kuviota ovat pisteen suhteen symmetrisiä, jos niille voidaan piirtää symmetriakeskus siten, että kaikille kuvion pisteille löytyy vastinpiste vastaavalta etäisyydeltä symmetriakeskuksen toiselta puolelta. Symmetriakeskuksia voi olla vain yksi.

Siirto

Siirto on yhtenevyyskuvauksista ajatuksena yksinkertaisin. Siirrossa kuvion kaikki pisteet siirtyvät samaan suuntaan yhtä pitkän matkan. Kuvion kaikki mitat säilyvät siis alkuperäiseen verrattuna samoina, eli kuviot ovat ilmeisesti yhteneviä.

Jaksossa 5 opittiin siirtämään jana harpin avulla tiettyyn pisteeseen. Tätä samaa menetelmää hyödynnetään, kun siirretään kokonaisia suurempia kuvioita, kuten monikulmioita, paikasta toiseen.

Siirtosuunta voidaan ilmaista esimerkiksi nuolella, jonka suunta kertoo siirron suunnan, ja pituus siirrettävän matkan. Myöhemmin ainakin lukio-opinnoissa opitaan nuolen olevan vektori, jonka tärkeimmät ominaisuudet ovat siis suuruus ja suunta.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_siirto.ggb

Nyt siis siirretään siirron ilmaiseva nuoli (suuntajana, vektori) alkuperäisiin pisteisiin, jolloin siirtyneet pisteet löytyvät nuolien kärjistä.

Kierto

Kierto eli rotaatio kääntää kuviota jonkin kiertokeskuksen ympäri. Kiertokeskus voi olla jokin kuvion oma piste tai ulkoinen piste, esimerkiksi origo. Kierrettäessä tulee ilmoittaa kiertokeskuksen lisäksi kulma, jonka verran kuviota kierretään sekä kiertosuunta (myötä- vai vastapäivään). Alla olevassa animaatiossa voit kiertää kolmiota myötäpäivään haluamasi kulman verran. Näet kunkin kärkipisteen liikeradan valitsemalla pisteen vasemmasta ylälaidasta.

https://jannevenhoedu.github.io/ma7/j5/t/ma7j5_teoria_kierto.ggb

9. Yhdenmuotoisuus

Kuviota pienennettäessä tai suurennettaessa siihen liittyvät pituudet muuttuvat, mutta muoto ja mittasuhteet säilyvät samoina. Kuvioita kutsutaan tällöin yhdenmuotoisiksi. Monikulmioiden tapauksessa yhdenmuotoisuus tarkoittaa siis sitä, että monikulmion vastinkulmat säilyvät samoina, mutta vastinsivujen pituudet muuttuvat jossakin suhteessa. Yhdenmuotoisuutta merkitään $\sim$-merkillä, esimerkiksi merkintä $\textsf{kolmio ABC $\sim$ kolmio DEF}$ lausuttaisiin "Kolmio ABC on yhdenmuotoinen kolmion DEF kanssa".

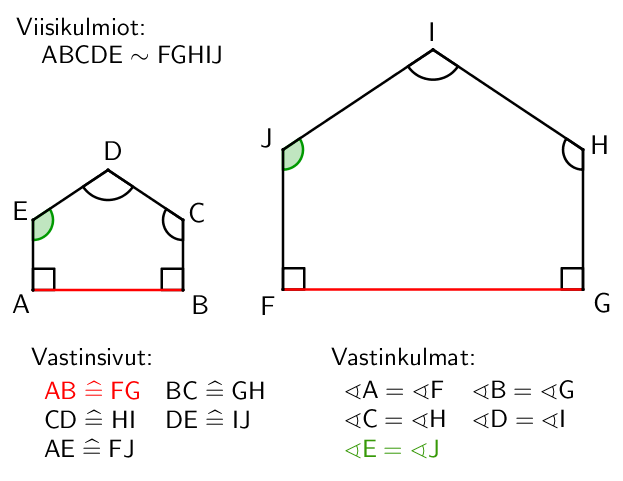
Suhde

Suhde merkitään joko murtolukuna tai erityisenä suhdelukuna, jossa käytetään jakolaskusta tuttua kaksoispiste $\textsf{:}$-merkintää. Esimerkiksi merkintä $\mathsf{1:4}$ lausutaan "yhden suhde neljään". Vastinsivuja voidaan merkitä $\widehat{=}$-merkillä, joka lausutaan "vastaa". Esimerkiksi vastinjanoista voitaisiin merkitä $\textsf{AB $\widehat{=}$ CD}$, joka lausutaan "Jana AB vastaa janaa CD".

Esimerkki: Kolmio ABC on pienennetty, jolloin on saatu yhdenmuotoinen kolmio A'B'C'. Mikä on pienennetyn kolmion sivujen suhde alkuperäisen kolmion sivuihin?

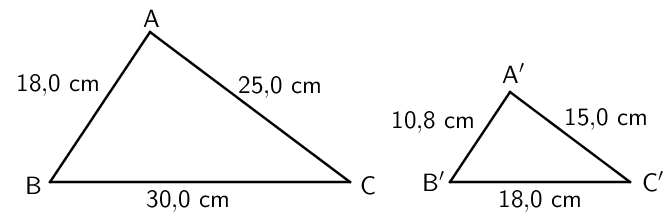
$\mathsf{\dfrac{A'B'}{AB} = \dfrac{\text{10,8 cm}}{\text{18,0 cm}} = \dfrac{3}{5} = 3 : 5}$

$\mathsf{\dfrac{B'C'}{BC} = \dfrac{\text{18,0 cm}}{\text{30,0 cm}} = \dfrac{3}{5} = 3 : 5}$

$\mathsf{\dfrac{A'C'}{AC} = \dfrac{\text{15,0 cm}}{\text{25,0 cm}} = \dfrac{3}{5} = 3 : 5}$

Vastaus: Kolmioiden A'B'C' ja ABC sivujen suhde on 3 : 5.

Mittakaava

Muuttuneen kuvion (kuva) ja alkuperäisen kuvion sivujen pituuden suhdetta kutsutaan mittakaavaksi. Mittakaavaa merkitään usein muuttujalla $\textsf{k}$.

$\mathsf{k = \dfrac{\text{kuva}}{\text{alkuperäinen}}}$

Mittakaavaa käytetään esimerkiksi kartoissa. Kartta pyrkii siis olemaan yhdenmuotoinen kuva maastosta ylhäältä päin kuvattuna. Esimerkiksi rakennusten välisten etäisyyksien suhteet ovat samat kartassa ja luonnossa. Toki huomautuksena on mainittava suurta aluetta (maat ja mantereet) kuvaavien karttojen ongelmana maapallon pinnan pyöreys verrattuna karttapaperin tasaisuuteen.

Mittakaavan määrittäminen

Kartan tai jonkin muun muutoksen mittakaavaa määrittäessä täytyy tietää kohteen todellinen pituus, ja vastaava pituus kuvassa (kartalla). Mittakaava saadaan siis näiden pituuksien suhteena. Muodostunut jakolasku (murtoluku) tulee supistaa mahdollisimman yksinkertaiseksi.

Esimerkki: Eräästä kartasta mitattiin Viljakkalan Yhtenäiskoulun ja kirkon väliseksi etäisyydeksi 12 cm linnuntietä kuljettuna. Luonnossa tämän etäisyyden tiedetään olevan 900 m. Mikä on kartan mittakaava?

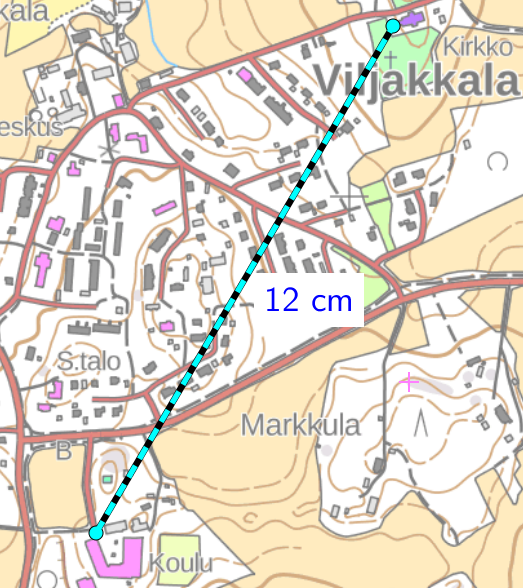
Muutetaan pituudet samaan yksikköön:

Pituus kuvassa: 12 cm

Pituus luonnossa: 900 m = 90 000 cm

Lasketaan mittakaava:

$\require{cancel}\begin{align}\mathsf{k} =& \mathsf{\dfrac{\text{pituus kuvassa}}{\text{pituus luonnossa}}}\\ =& \mathsf{\dfrac{\text{12 }\cancel{cm}}{\text{90 000 }\cancel{cm}}}\\ =& \mathsf{\dfrac{1}{7500}}\\ =& \mathsf{1 : 7\;500}\end{align}$

Vastaus: Kartan mittakaava on 1 : 7 500.

Mittakaavan käyttö

Yleisempi käyttökohde mittakaavalle on tilanne, jossa tunnetaan kartan mittakaava, ja sen avulla arvioidaan kohteiden välistä etäisyyttä luonnossa.

Esimerkki: Kartasta mitattiin Hervannan Ahvenisjärven pituudeksi 6,8 cm. Kartan mittakaava on 1 : 5000. Kuinka pitkä Ahvenisjärvi on oikeasti?

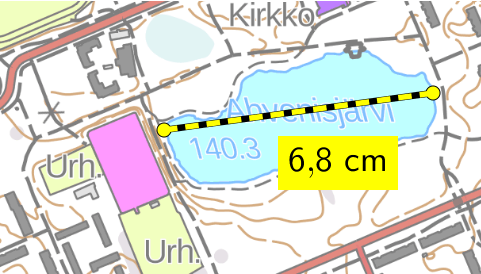
Lasketaan, kuinka monta metriä 1 cm vastaa kartalla:

$\mathsf{\text{1 cm}\;\widehat{=}\;\text{5000 cm} = \text{50 m}}$

Lasketaan 6,8 cm vastaava pituus:

$\mathsf{\text{6,8} \cdot \text{50 m} = \text{340 m}}$

Vastaus: Ahvenisjärvi on 340 metriä pitkä.

Toinen tilanne, jossa mittakaavaa tarvitaan, on jonkin todellisen kohteen piirtäminen pienennettynä tai suurennettuna.

Esimerkki: Varastohalli on 8,0 metriä leveä ja 12,5 metriä pitkä. Hallista piirretään pohjapiirrustus mittakaavassa 1 : 50. Mitkä ovat hallin mitat kuvassa?

Mittakaavasta: $\mathsf{\text{1 cm}\;\widehat{=}\;\text{50 cm} = \text{0,5 m}}$

Leveys (cm):

$\mathsf{\dfrac{\text{8,0 m}}{\text{0,5 m}} = 16}$

Pituus (cm):

$\mathsf{\dfrac{\text{12,5 m}}{\text{0,5 m}} = 25}$

Vastaus: Hallin leveys kuvassa on 16 cm ja pituus 25 cm.