MA7 Jakso 3: Kirjainlaskenta
1. Muuttujalauseke
Käsitteitä
Muuttuja - Tuntematon luku, jota merkitään kirjaimella.
\(\mathsf{a, b, c, x, y, z, \alpha, \beta, \gamma}\)
Lauseke - Yksi tai useampi laskutoimitus.
\(\mathsf{5 \cdot 4 + 2}\)
Muuttujalauseke - Lauseke, jossa esiintyy muuttujia.
\(\mathsf{2 \cdot x + 3}\)
Muuttujan arvo - Esimerkiksi mittaamalla saatu luku, jolla muuttuja voidaan korvata.
\(\mathsf{x = 5}\)
Sijoittaminen - Muuttujan korvaaminen muuttujan arvolla.
\(\begin{align}\phantom{=}&\mathsf{2 \cdot {\color{red}x} + 3 \qquad {\color{red}x = 5}} \\ =\;&\mathsf{2\cdot {\color{red}5} + 3}\end{align}\)
Lausekkeen arvo - Muuttujalausekkeen lopullinen vastaus, kun muuttujan arvo on sijoitettu lausekkeeseen.
\(\mathsf{2 \cdot 5 + 3 = 10 + 3 = 13}\)
Sieventäminen - Muuttujalausekkeen kirjoittaminen yksinkertaisempaan (siistimpään, sievempään) muotoon
\(\mathsf{-1 \cdot x = -x}\)
Termi - Kertoimen ja muuttujaosan muodostama kokonaisuus. Sievennetty luvun ja muuttujan kertolaskusta.
\(\mathsf{4x}\)
Kerroin - Termin alussa oleva luku. Jos kerroin on 1 tai -1, jätetään 1 merkitsemättä.
\(\mathsf{{\color{red}4}x}\)
Muuttujaosa - Termissä oleva muuttuja (kirjain). 8. luokalla voi sisältää jo useampia muuttujia.
\(\mathsf{4{\color{red}x}}\)
Yhtälö - Kaksi (muuttuja)lauseketta merkitty yhtä suureksi.
\(\mathsf{3 \cdot x - 1 = x + 3}\)
Yhtälön ratkaisu - Muuttujan arvo, jolla yhtäsuuruus pätee.
\(\begin{align}\mathsf{3 \cdot x - 1} &= \mathsf{x + 3} \\ \mathsf{3 \cdot 2 - 1} & = \mathsf{2 + 3} \\ \mathsf{5} &= \mathsf{5} \end{align} \)
Yhtälön ratkaiseminen - Menetelmä, jonka avulla etsitään muuttujan arvoa, joka on yhtälön ratkaisu.
\(\begin{align} \mathsf{3x - 1} &= \mathsf{x + 3} \qquad &&\mathsf{\|+1} \\ \mathsf{3x} &= \mathsf{x + 4} &&\mathsf{\|-x} \\ \mathsf{2x} &= \mathsf{4} &&\mathsf{\|:2} \\ \mathsf{x} &= \mathsf{2} \end{align}\)
Muuttujalausekkeen muodostaminen
Matematiikassa kirjaimia käytetään tuntemattoman tai muuttuvan luvun esittämiseen. Tämän vuoksi niitä kutsutaan muuttujiksi. Muuttujien avulla voidaan erilasiia sääntöjä ja riippuvuuksia kirjoittaa matemaattisiksi laskulausekkeiksi eli muuttujalausekkeiksi.
Esimerkki: Kirjoita kuvausta vastaava muuttujalauseke.
a) Muuttujaa \(\mathsf{x}\) kerrotaan luvulla 5 ja tuloon lisätään luku 2.
\(\mathsf{x \cdot 5 + 2}\)
b) Suorakulmion pinta-ala \(\mathsf{A}\) lasketaan kertomalla suorakulmion leveys \(\mathsf{a}\) korkeudella \(\mathsf{b}\)
\(\mathsf{A = a \cdot b}\)
c) Keskinopeus \(\mathsf{v}\) lasketaan jakamalla matka \(\mathsf{s}\) ajalla \(\mathsf{t}\)
\(\mathsf{v = \dfrac{s}{t}}\)
d) Pekka on kolme vuotta vanhempi kuin Tiina
\(\mathsf{p = t + 3}\),
missä \(\mathsf{p}\) kuvaa Pekan ikää vuosina, ja \(\mathsf{t}\) kuvaa Tiinan ikää vuosina.
Muuttujalausekkeen arvon laskeminen
Muuttujalausekkeilla voidaan siis kuvata sääntöjä ja asioiden välisiä riippuvuuksia yleisellä tasolla ottamatta kantaa yksittäisiin tilanteisiin. Hyödylliseksi säännöt muuttuvat, kun meille selviää (esim. mittaamalla) muuttujan arvo. Tällöin muuttujalausekkeeseen voidaan sijoittaa muuttujan paikalle saatu arvo, ja laskea lausekkeen arvo.
Esimerkki: Laske edellisen esimerkin lausekkeiden arvot annetuilla muuttujien arvoilla.
a) Laske muuttujalausekkeen \(\mathsf{x \cdot 5 + 2}\) arvo, kun \(\mathsf{\color{red}x = 3}\).
\(\mathsf{{\color{red}x} \cdot 5 + 2 = {\color{red}3} \cdot 5 + 2 = 15 + 2 = 17}\)
Vastaus: Muuttulausekkeen arvo on 17.
b) Laske suorakulmion pinta-ala, kun suorakulmion leveys \(\mathsf{\color{red}{a = \text{5,4 cm}}}\) ja korkeus \(\mathsf{ \color{blue}{b = \text{2,0 cm}}}\).
\(\mathsf{A = {\color{red}a} \cdot {\color{blue}b} = {\color{red}\text{5,4 cm}} \cdot {\color{blue}\text{2,0 cm}} = \text{10,8 cm}^2}\)
Vastaus: Suorakulmion pinta-ala on 10,8 cm2.
c) Laske keskinopeus, kun pyöräilijän kulkema matka \(\mathsf{{\color{red}s = \text{72 km}}}\) ja aika \(\mathsf{{\color{blue}t = \text{3 h}}} \).
\(\mathsf{v = \dfrac{\color{red}s}{\color{blue}t} = \dfrac{\color{red}\text{72 km}}{\color{blue}\text{3h}} = \text{24 km/h}}\)
Vastaus: Pyöräilijän keskinopeus on 24 km/h.
d) Kuinka vanha Pekka on, kun Tiina on 41-vuotias? (Nyt siis \(\mathsf{\color{red}t = 41}\))
\(\mathsf{p = {\color{red}t} + 3 = {\color{red}41} + 3 = 44}\)
Vastaus: Pekka on 44-vuotias.
2. Termi
Merkintä
Usein matematiikan merkinnöissä muuttujalausekkeista jätetään kertomerkki merkitsemättä. Tämä on vain merkintäsopimus. Esimerkiksi muuttujalauseke \(\mathsf{5 \cdot x}\) voidaan kirjoittaa siis yksinkertaisesti \(\mathsf{5x}\). Algebrassa tällaista luvun ja kirjaimen välistä kertolaskua kutsutaan termiksi. Lukua kutsutaan termin kertoimeksi ja kirjainta termin muuttujaosaksi.
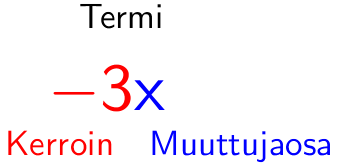
Esimerkki: Sievennä.
a) \(\mathsf{4 \cdot a = 4a}\)
b) \(\mathsf{-3 \cdot z = -3z}\)
c) \(\mathsf{1 \cdot x = x}\)
d) \(\mathsf{-1 \cdot b = -b}\)
Kuten esimerkistä huomataan, kerrointa 1 ei merkitä näkyviin, ja kertoimesta -1 jää näkyviin ainoastaan miinusmerkki.
Vakiotermi
Myös luku ilman muuttujaosaa on termi. Tällaista termiä kutsutaan vakiotermiksi. Vakiotermejä voi olla esimerkiksi -3, 2 tai 9. Vakiotermi pysyy nimensä mukaisesti aina samana, koska siinä ei ole muuttujaa, joka vaikuttaisi termin arvoon sitä laskettaessa.
Termeistä muuttujalausekkeita
Monet muuttujalausekkeet voidaan kirjoittaa termien summana. Esimerkiksi muuttujalausekkeessa \(\mathsf{-8x+5}\) on kaksi termiä \(\mathsf{-8x}\) ja \(\mathsf{+5}\). Lausekkeessa termit järjestellään muuttujaosan mukaiseen aakkosjärjestykseen. Vakiotermit laitetaan viimeiseksi. Esim. \(\mathsf{3a + 4b - 6c + 7}\).
Muuttujalausekkeen arvoa laskettaessa tulee muistaa lisätä kertomerkki omalle paikalleen sijoitusvaiheessa.
Esimerkki: Laske muuttujalausekeen \(\mathsf{-8x+6}\) arvo, kun
a) \(\mathsf{\color{red}x = 4}\)
\(\mathsf{-8{\color{red}x}+6 = -8 \cdot {\color{red}4} + 6 = -32 + 6 = -26}\)
b) \(\mathsf{\color{blue}{x = -2}}\)
\(\mathsf{-8{\color{blue}x}+6 = -8 \cdot {\color{blue}(-2)} + 6 = 16 + 6 = 22}\)
3. Termien yhteen- ja vähennyslasku
Samanmuotoiset ja erimuotoiset termit
Jos kahden tai useamman termin muuttujaosa on täsmälleen sama, kutsutaan termejä samanmuotoisiksi. Jos termien muuttujaosat ovat erilaiset, kutsutaan termejä erimuotoisiksi.
Esimerkki: Ovatko termit samanmuotoisia?
a) \(\mathsf{-3x}\), \(\mathsf{x}\) ja \(\mathsf{9x}\)
Termit ovat samanmuotoisia, koska niillä on sama muuttujaosa \(\mathsf{x}\).
b) \(\mathsf{-b}\), \(\mathsf{2b}\) ja \(\mathsf{-2}\)
Termit eivät ole samanmuotoisia, koska kolmas termi on vakiotermi, ja muiden muuttujaosa on \(\mathsf{b}\).
Termien yhteen- ja vähennyslasku
Vain samanmuotoisia termejä voidaan laskea yhteen tai vähentää toisistaan. Termien yhteenlaskussa termien kertoimet lasketaan yhteen ja vähennyslaskussa vähennetään tosiistaan.
Esimerkki: Sievennä.
a) \(\mathsf{{\color{red}4}x + {\color{red}3}x = {\color{red}7}x}\)
Termit ovat samanmuotoisia, joten voidaan sieventää laskemalla kertoimet yhteen.
b) \(\mathsf{5a - 3b}\)
Termit eivät ole samanmuotoisia, joten ei voida sieventää.
c) \(\mathsf{{\color{red}5}a - {\color{red}3}a = {\color{red}2}a}\)
Termit ovat samanmuotoisia, joten voidaan sieventää vähentämällä kertoimet toisistaan.
d) \(\mathsf{{\color{red}4a}{\color{blue}\;-\; 3b}{\color{red}\;-\;a}{\color{blue}\;+\;7b} = {\color{red}3a}{\color{blue}\;+\;4b}}\)
Keskenään samanmuotoiset termit voidaan sieventää.
4. Termien kerto- ja jakolasku
Kaksi termiä voidaan myös kertoa tai jakaa keskenään. Kertolaskussa kertoimet kerrotaan keskenään, ja muuttujaosat kerrotaan keskenään. Jakolaskussa toimitaan samalla periaatteella kuin kertolaskussakin, eli termien kertoimet jaetaan keskenään, ja muuttujaosat jaetaan keskenään.
7. luokalla keskitymme kertomaan ja jakamaan muuttujatermiä vain vakiotermeillä, eli jätetään muuttujaosien käsittely 8. luokalle ja kultapaketin tehtäviin.
Esimerkki: Sievennä.
a) \(\mathsf{{\color{red}4} \cdot {\color{red}5}x = {\color{red}20}x}\)
b) \(\mathsf{{\color{red}-3}x \cdot ({\color{red}-5}) = {\color{red}15}x}\)
c) \(\mathsf{\dfrac{{\color{red}42}x}{\color{red}7} = {\color{red}6}x}\)
d) \(\mathsf{\dfrac{{\color{red}-32}x}{{\color{red}8}x} = {\color{red}-4}}\)
Huomaa esimerkin d-kohdassa, että muuttujien jakolasku \(\mathsf{\dfrac{x}{x} = 1}\), jolloin muuttujaosa supistuu vastauksesta pois.
Lisätietoa: Kertominen ja jakaminen muulla kuin vakiotermillä
Jos molemmissa termeissä on muuttujaosa, tulee ymmärtää mitä kahden muuttujan välinen kerto- ja jakolasku tarkoittavat. Tähän käytetään potenssimerkintää, joka on merkintätapa saman luvun (tai muuttujan) toistuvalle kertolaskulle.
Esimerkki: Merkitse potenssimerkintänä.
a) \(\mathsf{4 \cdot 4 \cdot 4 = 4^3}\)
b) \(\mathsf{x \cdot x \cdot x \cdot x = x^4}\)
Esimerkin a-kohdassa potenssimerkinnän oikeassa ylänurkassa oleva pienempi 3 kuvaa, kuinka monta kertaa luku 4 kerrotaan itsensä kanssa. Esimerkin b-kohdassa vastaavasti on neljä kertaa muuttuja x kerrottu itsensä kanssa, joten eksponentiksi (pieni luku yläkulmassa) kirjoitetaan neljä.
Nyt kun termejä siis kerrotaan keskenään, kerrotaan erikseen kertoimet (luvut) ja muuttujat (kirjaimet). Jakolaskussa muuttujaosasta voidaan supistaa pois muuttujia yhtä monta.
Esimerkki: Sievennä.
a) \(\mathsf{{\color{red}4}{\color{blue}x} \cdot {\color{red}5}{\color{blue}x} = {\color{red}20}{\color{blue}x}^2}\)
b) \(\mathsf{\require{cancel}\dfrac{24x^2}{8x} = \dfrac{24 \cdot x \cdot \cancel{x}}{8 \cdot \cancel{x}} = 3x}\)
5. Lukujonot
Merkintä
Lukujono on järjestykseen asetettujen lukujen luettelo. Yksittäistä lukua kutsutaan jonon jäseneksi. Jokaisella jäsenellä on oma järjestysnumeronsa, jota merkitään usein muuttujalla \(\mathsf{n}\). Jos lukujonolle annetaan nimeksi \(\mathsf{a}\), niin lukujonoa merkitään \(\mathsf{(a_n)}\), ja esimerkiksi neljättä jäsentä (\(\mathsf{n=4}\)) merkitään \(\mathsf{a_4}\).
Esimerkki: Tarkastellan lukujonoa \(\mathsf{(a_n) = (2, 5, 8, 11,...)}\).
a) Määritä jonon toinen jäsen.
\(\mathsf{a_2 = 5}\)
b) Määritä jonon ensimmäinen jäsen.
\(\mathsf{a_1 = 2}\)
c) Määritä jonon neljäs jäsen.
\(\mathsf{a_4 = 11}\)
Lukujono voi olla päättyvä, esimerkiksi (2, 3, 4, 5) tai päättymätön, (2, 3, 4, 5,...). Päättymättömän lukujonon tunnistaa kolmesta pisteestä lukujonon lopussa.
Lukujonon säännön muodostaminen
Lukujonon sääntö voidaan muodostaa kahdella eri tavalla:
- Sanallisesti ilmoittamalla lukujonon ensimmäinen jäsen sekä laskutoimitus, jolla seuraava jäsen lasketaan.
- Lausekkeella, jolla voidaan laskea lukujonon järjestykseltään \(\mathsf{n}\):s jäsen.
Esimerkki: Tarkastellaan lukujonoa \(\mathsf{(a_n) = (2, 5, 8, 11,\dots)}\). Ilmoita lukujonon sääntö
a) sanallisesti
Lukujonon ensimmäinen jäsen on \(\mathsf{2}\), ja seuraava jäsen saadaan lisäämällä edelliseen luku \(\mathsf{3}\).
b) lausekkeena
\(\mathsf{a_n = 3n-1}\)
Aritmeettinen ja geometrinen lukujono
Lukujono voi olla millainen tahansa. Täysin satunnaisia lukujonoja käytetään, kun halutaan satunnaisuutta matemaattisissa malleissa tai simulaatioissa. Yleensä meitä kuitenkin kiinnostaa jonkin säännön mukaan muodostettu lukujono. Peruskoulun matematiikassa tutustutaan kahteen lukujonotyyppiin, jotka on helppo ymmärtää tuttujen peruslaskutoimitusten avulla.
Aritmeettinen lukujono
Aritmeettinen lukujono on sellainen lukujono, jonka seuraava jäsen saadaan lisäämällä tai vähentämällä edelliseen jäseneen aina sama luku.
Esimerkki: Ilmoita lukujonon sääntö sanallisesti.
a) \(\mathsf{(5, 7, 9, 11, 13,...)}\)
Lukujonon 1. jäsen on 5, ja seuraava saadaan lisäämällä edelliseen luku 2.
b) \(\mathsf{(5, 1, -3, -7, -11,...)}\)
Lukujonon 1. jäsen on 5, ja seuraava saadaan vähentämällä edellisestä luku 4.
Geometrinen lukujono
Geometrinen lukujono on sellainen lukujono, jonka seuraava jäsen saadaan kertomalla tai jakamalla edellinen jäsen aina samalla luvulla.
Esimerkki: Ilmoita lukujonon sääntö sanallisesti.
a) \(\mathsf{2, 4, 8, 16, 32, 64,...}\)
Lukujonon 1. jäsen on 2, ja seuraava jäsen saadaan kertomalla edellinen luvulla 2.
b) \(\mathsf{10\,000, 1000, 100, 10, 1,...}\)
Lukujonon 1. jäsen on 10 000, ja seuraava jäsen saadaan jakamalla edellinen luvulla 10.
Jos lukujonon jäsenissä on desimaalilukuja, tällöin jäsenten väliin kirjoitetaan luettelomerkiksi puolipiste ( ; ) eikä pilkkua ( , ), jotta vältytään sekaannuksilta.
\(\mathsf{\text{0,4}; \text{0,6}; \text{0,8}; ...}\)
Lisätietoa: Fibonaccin lukujono
Fibonacci eli Leonardo Pisano (s. 1170 - 1180, k. 1250) oli italialainen matemaatikko, joka oli ensimmäisiä länsimaalaisia merkittäviä matemaatikoita. Hän kirjoitti kuuluisan teoksensa Liber abbaci vuonna 1202, joka oli ensimmäisiä kymmenjärjestelmän oppaita. Hän on kuitenkin kaikkein tunnetuin nimeään kantavan lukujonon vuoksi. Lukujono esiteltiin Liber abbacissa kanien lisääntymistehtävän ratkaisuna.
Kuinka monta kaniparia syntyy vuodessa, jos vuoden alussa on yksi pari ja jokainen pari synnyttää joka kuukausi uuden parin, joka alkaa synnyttää kahden kuukauden kuluttua?
Fibonaccin lukujonossa seuraava jäsen saadaan laskemalla kaksi edellistä jäsentä yhteen. Lukujonon kaksi ensimmäistä jäsentä ovat 1 ja 1. Näin ollen lukujonon ensimmäiset jäsenet ovat
\(\mathsf{(f_n) = (1, 1, 2, 3, 5, 8, 13, ...)}\)
1. jäsen: \(\mathsf{f_1 = 1}\)
2. jäsen: \(\mathsf{f_2 = 1}\)
3. jäsen: \(\mathsf{f_3 = f_1 + f_2 = 1+1 = 2}\)
4. jäsen: \(\mathsf{f_4 = f_2 + f_3 = 1+2=3}\)
5. jäsen: \(\mathsf{f_5 = f_3 + f_4 = 2+3=5}\)
6. jäsen: \(\mathsf{f_6 = f_4 + f_5 = 3+5=8}\), jne.
Fibonaccin lukujono on kiinnostava, koska luonnosta on löydettävissä lukujonon mukaista käytöstä mm. puiden oksista ja lehdistä sekä ananaksen ja käpyjen kierteistä. Havainnollistavia kuvia lisääntymistehtävästä ja biologisista sovelluksista mm. englanninkielisen Wikipedian artikkelissa.
6. Lisätietoa: Yhtälön ratkaiseminen
Yhtälö
Yhtälöllä tarkoitetaan tilannetta, jossa kaksi lauseketta on merkitty yhtä suuriksi. Esimerkiksi yhtälössä \(\mathsf{2x-4 = -x + 5}\) lausekkeet \(\mathsf{2x-4}\) ja \(\mathsf{-x+5}\) saavat siis saman arvon jollakin muuttujan \(\mathsf{x}\) arvolla. Muuttujan \(\mathsf{x}\) arvo saadaan selvitettyä ratkaisemalla yhtälö. Tästä lisää otsikon "Yhtälön ratkaiseminen" alla.
Yhtälöitä käytetään matemaattisissa aineissa (matematiikkan, fysiikka, kemia, tietotekniikka) paljon. 8. luokalla opiskellaan ns. 1. asteen ja 2. asteen yhtälöitä sekä verrantoja, ja 9. luokalla laajennetaan 8. luokan tietämystä yhtälöpareihin sekä epäyhtälöihin. Fysiikan puolella tutustutaan erilaisiin luonnonlakeihin laskukaavojen avulla, joita voidaan muokata käyttötarkoitukseen sopiviksi yhtälöratkaisun menetelmin.
Peruskoulun jälkeen on lukiossa ja eri korkeakouluissa mahdollista opiskella lineaarisia yhtälöryhmiä, joita käytetään esim. GPS-paikannuksessa ja tietokonegrafiikassa tai differentiaali- sekä osittaisdifferentiaaliyhtälöitä, joita käytetään mm. monimutkaisemmissa matemaattisissa malleissa, kuten sään ennustuksessa.
7. luokalle sopiva tilanne voisi olla sellainen, että tiedetään lausekkeen arvo, mutta ei tiedetä, millä muuttujan arvolla se on saatu laskettua. Esimerkiksi yhtälön \(\mathsf{2x + 1 = 7}\) ratkaisu saadaan selvittämällä, mikä luku sopii muuttuja \(\mathsf{x}\) paikalle.
Yhtälön ratkaiseminen
Yhtänlönratkaisussa on tavoitteena selvittää muuttujan \(\mathsf{x}\) arvo, jolla yhtälö on tosi, eli yhtäsuuruus pätee. Yhtälöt voidaan ratkaista päättelemällä, mutta varmin ja helpoin tapa on ratkaista yhtälö vaiheittain lisäämällä, vähentämällä, kertomalla tai jakamalla yhtälöä puolittain sopivilla luvuilla. Vaiheittain etenemällä saadaan lisäksi ratkaisulle perustelu ja löydetään kaikki mahdolliset ratkaisut. Tämän vuoksi päättely ei enää käy kuin saadun ratkaisun järkevyyden tarkasteluun.
Yhtälöä voidaan siis muokata suorittamalla sama laskutoimitus yhtälön molemmille puolille. Laskutoimitus on tärkeätä suorittaa molemmille puolille yhtälöä, koska tällöin oikean ja vasemman puolen yhtäsuuruus pysyy voimassa. Yhtälön ratkaiseminen loppuu, kun muuttuja \(\mathsf{x}\) on saatu jäämään yksin vain yhtälön toiselle puolelle.
Laskutoimitus, joka yhtälön molemmille puolille kullakin rivillä tehdään, merkitään rivin loppuun kahden pystyviivan \(\|\) oikealle puolelle. Laskutoimitusten muokkaama uusi yhtälö kirjoitetaan edellisen alapuolelle siten, että yhtäsuuruusmerkit ovat samassa pysysuorassa linjassa.
Yhtälön ratkaiseminen jakamalla puolittain
Tarkastellaan yhtälöä
\(\mathsf{3x = 24}\)
Nyt siis muuttujaa \(\mathsf{x}\) on kerrottu luvulla 3, vastaukseksi on saatu 24. Tästä on toki helppoa päätellä, että muuttujan x on oltava 8, koska \(\mathsf{3 \cdot 8 = 24}\). Ratkaisu saadaan käänteisesti jakolaskun avulla: \(\mathsf{24:3=8}\), koska jakolasku on kertolaskun käänteinen laskutoimitus. Yhtälöratkaisun menetelmien avulla ratkaisu näyttäisi seuraavalta.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{3x} &= \mathsf{24} \quad &&\mathsf{\|\color{red}:3}\\ \mathsf{x} &= \mathsf{8}\end{align}\)
1. rivillä on siis alkuperäinen yhtälö \(\mathsf{3x = 24}\). Pystyviivojen \(\|\) jälkeen on laskutoimitus, joka yhtälön molemmille puolille tehdään.
2. rivillä nähdään laskutoimituksen tulos. Vasemmalla on siis laskettu \(\mathsf{3x\;{\color{red}: 3} = x}\) ja oikealla \(\mathsf{24\;{\color{red}: 3}=8}\). Näin yhtälö on saatu ratkaistua, ja ratkaisuksi on saatu edellä päätelty \(\mathsf{x = 8}\).
Yhtälön ratkaiseminen lisäämällä tai vähentämällä puolittain
Tarkastellaan yhtälöä
\(\mathsf{x - 4 = 5}\)
Nyt muuttujasta x on vähennetty luku 4. Käytetään apuna jälleen käänteistä laskutoimitusta, joka vähennyslaskulle on tietenkin yhteenlasku. Lisäämällä yhtälön molemmille puolille luku 4, saadaan yhtälön vasemmalla puolella -4 häviämään nollaksi. Yhtälönratkaisun merkinnöin saadaan siis
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{x - 4} &= \mathsf{5}\quad &&\mathsf{\|\color{red}+4}\\ \mathsf{x} &= \mathsf{9}\end{align}\)
Vasemmalla laskettiin nyt \(\mathsf{x - 4 {\color{red}\;+\;4} = x}\) ja oikealla \(\mathsf{5{\color{red}\;+\;4} = 9}\). Ratkaisuksi saatiin siis \(\mathsf{x = 9}\), joka voidaan tarkistaa sijoittamalla ratkaisu alkuperäiseen yhtälöön. \(\mathsf{x-4 = 9-4 = 5}\).
Myös termejä, joissa esiintyy muuttuja x voidaan lisätä ja vähentää puolittain. Tarkastellaan yhtälöä
\(\mathsf{3x = x + 8}\)
Nyt molemmilla puolilla yhtälöä on termi, jossa esiintyy muuttuja x. Koska tavoitteena oli saada muuttuja x jäämään yksin vain yhtälön toiselle puolelle, poistetaan x toiselta puolelta. Tehdään se tällä kertaa yhtälön oikealta puolelta.
Esimerkki: Ratkaise yhtälö.
\(\begin{align}\mathsf{3x} &= \mathsf{x + 8}\quad &&\mathsf{\|\color{red}-x}\\\mathsf{2x} &= \mathsf{8}&&\mathsf{\|:2}\\ \mathsf{x} &= \mathsf{4}\end{align}\)
Vasemmalla saadaan siis \(\mathsf{3x{\color{red}\;-\;x} = 2x}\) ja oikealla \(\mathsf{x + 8 {\color{red}-x} = 8}\). Muuttujalle x jää vielä kerroin, joka saadaan poistettua aiemmin opitulla jakolaskulla puolittain.
Yhtälönratkaisu kokonaisuutena
Yhtälönratkaisusta opittiin edellä selvittämään kolme hieman erilaista tilannetta. Näitä kolmea menetelmää apuna käyttäen voidaan ratkaista mikä tahansa 1. asteen yhtälö enintään kolmella vaiheella. Alla olevassa vuokaaviossa on esitetty algoritmi yhtälönratkaisuun.
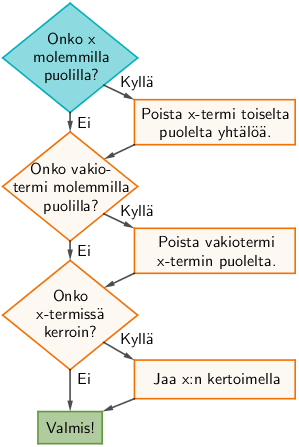
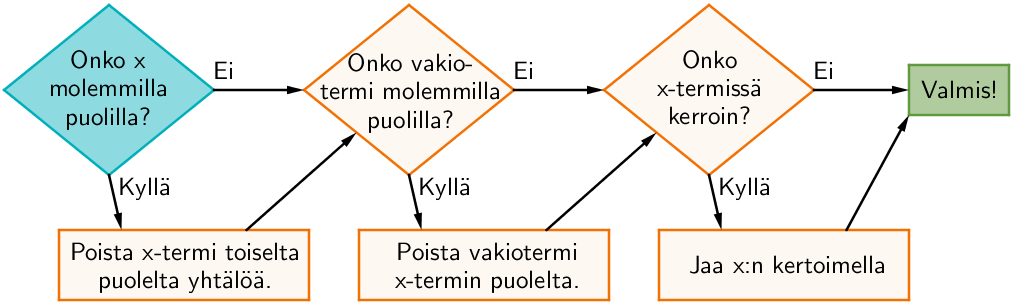
Esimerkki: Ratkaise yhtälö \(\mathsf{2x-4 = -x + 5}\) algoritmin avulla.
Onko x molemmilla puolilla? Kyllä on, joten poistetaan x-termi toiselta puolelta yhtälöä.
\(\begin{align}\mathsf{2x-4} &= \mathsf{-x+5}&&\mathsf{\|+x}\\\mathsf{3x-4} &= \mathsf{5}\end{align}\)
Onko vakiotermi molemmilla puolilla? Kyllä on, joten poistetaan vakiotermi x-termin puolelta.
\(\begin{align}\mathsf{3x-4} &= \mathsf{5}&&\mathsf{\|+4}\\\mathsf{3x} &= \mathsf{9}\end{align}\)
Onko x-termissä kerroin? Kyllä on, joten jaetaan x:n kertoimella.
\(\begin{align}\mathsf{3x} &= \mathsf{9}&&\mathsf{\|:3}\\\mathsf{x} &= \mathsf{3}\end{align}\)
Valmis!
Yhtälönratkaisun vastaus voidaan tarkistaa laskemalla erikseen vasemman ja oikean puolen lausekkeiden arvot. Niiden pitäisi olla siis yhtä suuret.
Esimerkki: Onko \(\mathsf{x=3}\) yhtälön \(\mathsf{2x-4=-x+5}\) ratkaisu?
Vasen: \(\mathsf{2x-4 = 2 \cdot 3 - 4 = 6 - 4 = 2}\)
Oikea: \(\mathsf{-x+5 = -3+5 = 2}\)
Vastaus: x = 3 on yhtälön ratkaisu.