MA7 Jakso 2: Jaollisuus ja murtoluvut
1. Jakolasku
Jakolasku
Jakolasku on käänteinen laskutoimitus kertolaskulle. Kertolaskun vastaus voidaan jakaa kertolaskun tekijällä, jolloin vastaus on toinen kertolaskun tekijä.
\( \mathsf{\color{blue}{3} \cdot \color{green}{5} = \color{red}{15} \qquad\qquad \dfrac{\color{red}{15}}{\color{blue}{3}} = \color{green}{5} \qquad\qquad \dfrac{\color{red}{15}}{\color{green}{5}} = \color{blue}{3}} \)
Jakolaskua voidaan merkitä joko jakoviivalla (eli murtolukuna) kuten yllä, kaksoispisteellä \(\mathsf{15:3=5}\) tai kauttaviivalla \(\mathsf{15/3=5}\).
Jakojäännös
Jakolasku ei mene aina tasan. Jakamatta jäänyttä osaa kutsutaan jakojäännökseksi.
Esimerkki: Laske jakojäännös.
a) \(\mathsf{\dfrac{12}{3} = 4}\)
Vastaus: Jakojäännös on 0.
b) \(\mathsf{\dfrac{13}{3} = 4 \text{ jää }1}\)
Vastaus: Jakojäännös on 1.
Jakolasku päässälaskuna
Tarkastellaan jakolaskua \(\mathsf{\dfrac{36}{3}}\). Jakolaskua voidaan lähteä tarkastelemaan parillakin eri tavalla.
- "Kuinka monta kertaa kolme mahtuu 36:een?"
\(\mathsf{\quad3+3+3+3+3+3+3+3+3+3+3+3 = 36}\) - "36 jaetaan kolmeen yhtä suureen osaan. Kuinka suuri on yksi osa?"
\(\mathsf{\quad 12 + 12 + 12 = 36}\)
Näin jakolaskun vastaukseksi saadaan 12.
Jakolasku osittain jakamalla
Jakolaskun voi jakaa myös pienempiin osiin helpottaakseen jakamista. Tarkoituksena on pilkkoa jaettava sellaiseksi summaksi (yhteenlaskuksi), että yksittäiset jakolaskut ovat helppoja laskea. Pilkkomisen voi kukin tehdä haluamallaan tavalla, kunhan jaettava tulee kokonaan summatuksi.
Esimerkki: Laske jakolasku osittain jakamalla.
a) \(\mathsf{\dfrac{445}{5} = \color{red}{\dfrac{400}{5}} + \color{blue}{\dfrac{45}{5}} = \color{red}{80} + \color{blue}{9} = 89}\)
b) \(\mathsf{\dfrac{144}{9} = \color{red}{\dfrac{90}{9}} + \color{blue}{\dfrac{54}{9}} = \color{red}{10} + \color{blue}{6} = 16}\)
c) \(\mathsf{\dfrac{1893}{3} = \color{red}{\dfrac{1800}{3}} + \color{blue}{\dfrac{90}{3}} + \color{green}{\dfrac{3}{3}} = \color{red}{600} + \color{blue}{30} + \color{green}{1} = 631}\)
Jakolasku allekkain ja jakokulmassa
Jakolasku, jossa jaettava on suuri ja jakaja on pieni, voidaan laskea allekkain tai jakokulmassa. Nämä menetelmät eroavat toisistaan vain hieman erilaisen merkinnän kautta.
Ideana on jakaa jaettavan luvun numerot osissa lähtien liikkelle vasemmanpuoleisimmasta numerosta. Seuraava numero lisätään edellisen jakolaskun jakojäännökseen, ja tätä toistetaan kunnes koko luku on käyty läpi. Esimerkki jakolaskusta allekkain:
Esimerkki jakolaskusta jakokulmassa:
2. Jaollisuus
Luku on jaollinen toisella luvulla, jos jako menee tasan, eli jakolaskusta ei jää jakojäännöstä.
Esimerkki:
a) Onko luku 13 jaollinen luvulla 4?
\( \mathsf{13:4 = 3 \text{ jää } 1}\)
Vastaus: Luku 13 ei ole jaollinen luvulla 4.
b) Onko luku 21 jaollinen luvulla 3?
\(\mathsf{21:3 = 7}\)
Vastaus: Luku 21 on jaollinen luvulla 3.
Jaollisuuden selvittäminen osittain jakamalla
Jakojäännöksen voi selvittää jakamalla jakolasku osiin. Tällöin jakamatta jääneen osan osoittaja kertoo jakojäännöksen.
Esimerkki: Onko luku 2345 jaollinen luvulla 3?
\(\begin{align}\mathsf{\dfrac{2345}{3}} &= \mathsf{\dfrac{2100}{3} + \dfrac{240}{3} + \dfrac{3}{3} + \dfrac{2}{3}}\\ &= \mathsf{700\ +\ 80\ +\ 1\ +\ \dfrac{\color{red}{2}}{3}}\\ &= \mathsf{781 \text{ jää } \color{red}{2}}\end{align}\)
Vastaus: Luku 2345 ei ole jaollinen luvulla 3.
Jaollisuuden selvittäminen jakamalla allekkain/jakokulmassa
Allekkain jakolaskussa viimeisen jakolaskun jälkeen jäävä jakojäännös on koko jakolaskun jakojäännös. Tällöin laskua ei siis lasketa desimaaliluvuille saakka, vaan laskeminen lopetetaan kun koko jaettava on käyty läpi. Alla on esimerkki jaollisuuden selvittämisestä allekkain jakolaskussa.
Esimerkki: Onko luku 5753 jaollinen luvulla 7?
Allekkain jakolasku

Jakokulma

Koska jakojäännös on suurempi kuin 0, jako ei mene tasan.
Vastaus: Luku 5753 ei ole jaollinen luvulla 7.
Jaollisuussäännöt
Kahden luvun välisen jaollisuuden voi selvittää myös ilman jakolaskun laskemista. Pienille numeroille on olemassa omat päättelysääntönsä, joiden avulla voidaan jaollisuus päätellä.
Jaollisuus voidaan päätellä luvun viimeisen numeron perusteella. Luku on jaollinen luvulla
- 2, jos luvun viimeinen numero on 0, 2, 4, 6, tai 8, eli luku on parillinen
- 5, jos luvun viimeinen numero on 0 tai 5
- 10, jos luvun viimeinen numero on 0.
Esimerkki: Tutki luvun jaollisuutta luvuilla 2, 5 ja 10.
a) 3204
Luku 3204 on jaollinen luvulla 2, koska viimeinen numero on 4.
b) 2930
Luku 2930 on jaollinen luvuilla 2, 5 ja 10, koska viimeinen numero on 0.
c) 763
Luku 763 ei ole jaollinen luvuilla 2, 5 tai 10, koska viimeinen numero on 3.
Jaollisuus voidaan päätellä luvun numeroiden summan perusteella. Luku on jaollinen luvulla
- 3, jos luvun numeroiden summa on jaollinen luvulla 3
- 9, jos luvun numeroiden summa on jaollinen luvulla 9.
Esimerkki: Tutki luvun jaollisuutta luvuilla 3 ja 9.
a) 2318
Luku 2318 ei ole jaollinen luvuilla 3 tai 9, koska 2 + 3 + 1 + 8 = 14, joka ei ole jaollinen luvuilla 3 tai 9.
b) 2034
Luku 2034 on jaollinen luvuilla 3 ja 9, koska 2 + 0 + 3 + 4 = 9, joka on jaollinen luvuilla 3 ja 9.
Esimerkki: Millä luvuista 2, 3, 5, 9 ja 10 luku 435 on jaollinen?
Viimeinen numero on 5, joten 435 on jaollinen luvulla 5, mutta ei luvuilla 2 tai 10.
Numeroiden summa on 4 + 3 + 5 = 12, joten luku 435 on jaollinen luvulla 3, mutta ei luvulla 9.
Vastaus: Luku 435 on jaollinen (ainakin) luvuilla 3 ja 5.
Lisätietoa
Muidenkin lukujen jaollisuudelle on määritetty päättelysääntöjä. Näitä ei kuitenkaan peruskoulun matematiikassa vaadita osattavaksi. Näitä voi kuitenkin käyttää hyvinä harjoituksina erilaisten sääntöjen noudattamiselle.
Luku on jaollinen luvulla
- 4, jos sen kahden viimeisen numeron muodostama luku on jaollinen neljällä.
- 6, jos se on jaollinen sekä kahdella että kolmella.
- 7, jos luvun viimeinen numero kerrotaan kahdella, tämä vähennetään jäljelle jääneestä alkuperäisestä luvusta ja saatu erotus on jaollinen seitsemällä.
- 8, jos sen kolmen viimeisen numeron muodostama luku on jaollinen kahdeksalla.
Esimerkki: Millä luvuilla 2-10 luku 1512 on jaollinen?
Luku 1512 on jaollinen luvulla
- 2, koska viimeinen numero on 2
- 3, koska numeroiden summa on \(\mathsf{1 + 5 + 1+ 2 = 9}\), joka on jaollinen luvulla 3
- 4, koska kahden viimeisen numeron muodostama luku 12 on jaollinen neljällä: \(\mathsf{12 : 4 = 3}\)
- 6, koska luku on jaollinen luvuilla 2 ja 3
- 7, koska luku \(\mathsf{151-2\cdot 2 = 151-4 = 147}\) on jaollinen seitsemällä \(\mathsf{147 : 7 = 21}\)
- 8, koska luku 512 on jaollinen luvulla 8: \(\mathsf{\dfrac{512}{8} = 64}\)
- 9, koska numeroiden summa on \(\mathsf{1 + 5 + 1+ 2 = 9}\), joka on jaollinen luvulla 9.
Luku 1512 ei ole jaollinen luvuilla
- 5, koska viimeinen numero ei ole 0 tai 5
- 10, koska viimeinen numero ei ole 0.
3. Tekijöihin jakaminen
Luvun jakajia kutsutaan tekijöiksi. Tekijöistä voidaan muodostaa kertolasku, jonka vastaus luku on.
Esimerkki: Mitkä ovat luvun 12 tekijät?
Luku 12 on jaollinen luvuilla 1, 2, 3, 4, 6 ja 12.
Vastaus: Luvun 12 tekijät ovat 1, 2, 3, 4, 6 ja 12.
Tekijöihin jakaminen kertolaskun avulla
Tekijä-sana tulee kertolaskusta, jossa puhutaan kertojasta ja kerrottavasta, eli tulon tekijöistä. Tällöin on luonnollista, että luvun tekijöitä etsitään kertolaskun avulla. Luvussa 1 todettiin jakolaskun olevan käänteistä kertolaskulle, joten tekijöiden löytämiseksi etsitään kaikki kertolaskut, joiden vastaus kyseinen luku on.
Esimerkki: Etsi luvun 40 tekijät kirjoittamalla kaikki kertolaskut, joiden vastaus on 40.
\(\begin{align}\mathsf{40} &= \mathsf{1 \cdot 40}\\ &= \mathsf{2 \cdot 20}\\ &= \mathsf{4 \cdot 10}\\ &= \mathsf{5 \cdot 8}\end{align}\)
Vastaus: Luvun 40 tekijät ovat 1, 2, 4, 5, 8, 10, 20 sekä 40.
Suurin yhteinen tekijä
Kahden tai useamman kokonaisluvun suurin yhteinen tekijä (SYT) on suurin kokonaisluku, jolla kaikki nämä luvut ovat jaollisia. Ensin selvitetään lukujen tekijät, joista valitaan suurin yhteinen tekijä.
Esimerkki: Mikä on lukujen 12 ja 18 suurin yhteinen tekijä?
1. Etsitään luvun 12 tekijät:
\(\mathsf{12 = 1 \cdot 12 = 2 \cdot 6 = 3 \cdot 4}\)
Luvun 12 tekijät ovat 1, 2, 3, 4, 6 ja 12.
2. Etsitään luvun 18 tekijät:
\(\mathsf{18 = 1 \cdot 18 = 2 \cdot 9 = 3 \cdot 6}\)
Luvun 18 tekijät ovat 1, 2, 3, 6, 9 ja 18.
3. Etsitään suurin yhteinen tekijä: 6.
Vastaus: Lukujen 12 ja 18 suurin yhteinen tekijä on 6.
Suurinta yhteistä tekijää käytetään mm. murtolukujen supistamisessa. Kun supistajana käytetään osoittajan ja nimittäjän suurinta yhteistä tekijää, saadaan murtoluku supistettua yksinkertaisimpaan muotoon.
Esimerkki: Supista murtolukua \(\mathsf{\dfrac{12}{18}}\) osoittajan ja nimittäjän suurimmalla yhteisellä tekijällä.
Edellisen esimerkin nojalla lukujen 12 ja 18 suurin yhteinen tekijä on 6.
\(\mathsf{\dfrac{12}{18}^{(6} = \dfrac{2}{3}}\)
Lisätietoa: Pienin yhteinen jaettava
Pienin yhteinen jaettava (PYJ) on nimensä mukaisesti luku, joka on jaollinen kahdella halutulla luvuilla, ja on sen lisäksi pienin mahdollinen.
Aluksi etsitään lukujen alkutekijät (nämä esitellään luvussa 4), ja muodostetaan tulo, jossa on tekijöinä kaikkia edellä löydettyjä alkutekijöitä. Sama alkutekijä esiintyy tulossa yhtä monta kertaa kuin niitä enimmillään esiintyi lukujen alkutekijöissä.
Esimerkki: Etsi lukujen 18 ja 30 pienin yhteinen jaettava.
Luvun 18 alkutekijät ovat 2, 3 ja 3, sillä \(\mathsf{18 = 2 \cdot {\color{red}3} \cdot {\color{red}3}}\).
Luvun 30 alkutekijät ovat 2, 3 ja 5, sillä \(\mathsf{30 = 2 \cdot 3 \cdot 5}\).
Pienin yhteinen jaettava on \(\mathsf{2 \cdot {\color{red}3} \cdot {\color{red}3} \cdot 5 = 90}\)
Vastaus: Lukujen 18 ja 30 pienin yhteinen jaettava on 90.
Esimerkissä mukaan tuloon otetaan siis kaikki erilaiset alkutekijät 2, 3 ja 5 ja luku 3 tulee kahteen kertaan, koska se esiintyy luvun 18 alkutekijänä kaksi kertaa.
Pienintä yhteistä jaettavaa käytetään silloin, kun ollaan laskemassa murtolukujen yhteen- tai vähennyslaskua (kts. luku 7). Ennen varsinaista laskua, luvut tulee laventaa samannimisiksi. Murtolukujen nimittäjien pienin yhteinen jaettava on pienin yhteinen luku, johon molemmat nimittäjät voidaan laventaa.
Esimerkki: Laske.
Edellisen esimerkin nojalla lukujen 18 ja 30 pienin yhteinen jaettava on 90.
\(\mathsf{\rule{0pt}{1.4em}^{5)}\!\dfrac{5}{18} + \!\!\rule{0pt}{1.4em}^{3)}\!\dfrac{7}{30} = \dfrac{25}{90} + \dfrac{21}{90} = \dfrac{46}{90}^{(2}\!\! = \dfrac{23}{45}}\)
Pienimmän yhteisen jaettavan voi laskea myös laskukaavalla, missä lukujen tulon itseisarvo jaetaan lukujen suurimmalla yhteisellä tekijällä. Positiivisilla luvuilla itseisarvoa ei tarvita, mutta yleisesti se on siis muotoa.
\(\mathsf{pyj(a,b) = \dfrac{|a\cdot b|}{syt(a,b)}}\)
4. Alkuluvut
Alkuluvut ovat sellaisia lukua 1 suurempia positiivisia kokonaislukuja, jotka eivät ole jaollisia millään muilla luvuilla kuin itsellään ja luvulla yksi. Alkuluvut ovat siis jaottomia lukuja.
Esimerkki: Jaa luku tekijöihin ja tutki, onko kyseessä alkuluku.
a) 13
\(\mathsf{13 = 1 \cdot 13}\)
Luvun 13 tekijät ovat 1 ja 13.
Vastaus: Luku 13 on alkuluku.
b)
\(\mathsf{14 = 1 \cdot 14 = 2 \cdot 7}\)
Luvun 14 tekijät ovat 1, 2, 7 ja 14.
Alkutekijät ja tekijöihinjakopuu
Kun luku jaetaan tekijöhin siten, että kaikki tekijät ovat alkulukuja, kutsutaan näitä lukuja alkutekijöiksi.
Esimerkki: Jaa luvut alkutekijöihin.
a) 30
\(\mathsf{30 = 2 \cdot 3 \cdot 5}\)
Vastaus: Luvun 30 alkutekijät ovat 2, 3 ja 5.
b) 50
\(\mathsf{50 = 2 \cdot 5 \cdot 5}\)
Vastaus: Luvun 50 alkutekijät ovat 2, 5 ja 5.
c) 72
\(\mathsf{72 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}\)
Vastaus: Luvun 72 alkutekijät ovat 2, 2, 2, 3 ja 3.
Alkutekijät voidaan löytää päättelemällä, mutta suurten lukujen tapauksessa tehtävää helpottaa ns. tekijöihinjakopuu. Puun latvaan, eli ylimpään solmuun, kirjoitetaan luku, jonka alkutekijät halutaan selvittää. Luku jaetaan aina kahdeksi tekijäksi, jotka kirjoitetaan seuraaviin solmuihin. Tätä jatketaan, kunnes kaikki tekijät ovat alkulukuja. Saadut alkuluvut ovat alkuperäisen luvun alkutekijät.
Esimerkki: Etsi luvun 60 alkutekijät, ja kirjoita luku 30 alkutekijöidensä tulona.
Vastaus: \(\mathsf{60 = 2 \cdot 2 \cdot 3 \cdot 5}\)
Alkutekijät järjestellään luetteloon ja kertolaskuun aina pienimmästä suurimpaan. Näin nähdään parhaiten eri alkutekijöiden lukumäärä ja voidaan verrata luvun alkutekijöitä toisen luvun alkutekijöihin. Samoja alkutekijöitä voidaan ryhmitellä myös potenssien avulla esimerkiksi \(\mathsf{60 = 2^2 \cdot 3 \cdot 5}\). Potenssit opetetaan kuitenkin vasta myöhemmin, joten 7. luokalla riittää avoin kertolasku.
5. Murtoluku
Murtoluku
Murtoluvulla esitetään kokonaisen osia. Murtoluvussa merkitään kaksi kokonaislukua allekkain, ja niiden väliin laitetaan viiva. Ylempää lukua kutsutaan osoittajaksi ja alempaa nimittäjäksi. Nimittäjä nimittää osien suuruuden ja osoittaja osoittaa kyseisten osien lukumäärän.

Sekaluku
Sekaluvulla tarkoitetaan lukua, jossa on sekaisin kokonaisia ja osia. Tämä merkintä on havainnollinen, kun halutaan nähdä murtoluvun suuruusluokka nopeasti. Tämän vuoksi murtoluvuilla suoritetut laskutoimitukset muutetaan aina laskemisen jälkeen sekaluvuksi mikäli mahdollista.

Murtoluku sekaluvuksi
Murtoluvut voidaan muuttaa sekaluvuksi, jos osoittaja on suurempi kuin nimittäjä. Muutos selkeyttää varsinkin laskun vastausta. Muunnettaessa murtolukua sekaluvuksi suoritetaan jakolasku "Kuinka monta kertaa nimittäjä mahtuu osoittajaan". Jakolaskun vastaus muodostaa kokonaisosan, ja jakolaskun jakojäännös jää näkyville murto-osaan.
Esimerkki: Muuta murtoluku sekaluvuksi.
a) \(\mathsf{\dfrac{7}{3}}\)
Koska \(\mathsf{7 : 3 = {\color{red}2} \text{ jää } {\color{blue}1}}\), niin
\(\mathsf{\dfrac{7}{3} \,=\, {\color{red}2} \dfrac{{\color{blue}1}}{3}}\)
b) \(\mathsf{\dfrac{23}{4}}\)
Koska \(\mathsf{23:4 = {\color{red}5} \text{ jää } {\color{blue}3}}\), niin
\(\mathsf{\dfrac{23}{4} \,=\, {\color{red}5} \dfrac{{\color{blue}3}}{4}}\)
Sekaluku murtoluvuksi
Sekaluku tulee muuttaa murtoluvuksi silloin, kun sekaluvuilla halutaan laskea jotakin. Kokonaisosa aiheuttaa jo vähennyslaskussa virheen vaaraa, mutta kerto- ja jakolaskussa meno äityy villiksi jo pelkästä ajatuksesta. Muunnettaessa sekalukua murtoluvuksi muutetaan kokonaisosa murtolukumuotoon ja lisätään murto-osaan. Kokonaisosan muodostaman murtoluvun nimittäjäksi valitaan sama nimittäjä kuin murto-osalla, ja osoittaja saadaan kertomalla kokonaisosa kyseisellä nimittäjällä. Lopuksi tämä osoittaja ja murto-osan osoittaja lasketaan yhteen.
Esimerkki: Muuta sekaluku \(\mathsf{3\dfrac{2}{5}}\) murtoluvuksi.
\(\mathsf{\color{blue}{3} \color{red}{\dfrac{2}{5}} \,=\, \color{blue}{\dfrac{15}{5}} + \color{red}{\dfrac{2}{5}} \,=\, \dfrac{17}{5}}\)
Tämä opetataan yleensä yhdellä kertaa tehtäväksi laskutoimitukseksi, jota ei menetelmän opittuaan oppilaan tarvitse merkitä näkyviin. Pelkkä muutos riittää.
\(\mathsf{3 \dfrac{2}{5} \,=\, \dfrac{3 \cdot 5 + 2}{5} \,=\, \dfrac{17}{5}}\)
Murtoluku desimaaliluvuksi
Murtoluku voidaan muuttaa desimaaliluvuksi, jota kutsutaan myös murtoluvun arvoksi. Murtoluku on jakolasku, joka näkyy myös yhtenevästä merkintätavastakin. Murtolukujen avulla voidaan esittää selkeästi sellaisia kokonaisen osia, jotka desimaalilukuna olisivat pitkiä tai jopa päättymättömiä.
Esimerkki: Merkitse murtoluku desimaalilukuna.
a) \(\mathsf{\dfrac{3}{10} = 0{,}3}\)
b) \(\mathsf{\dfrac{16}{25} = 0{,}64}\)
c) \(\mathsf{\dfrac{1}{3} = 0{,}3333...}\)
Murtolukuja käytetään usein tarkkojen arvojen merkitsemiseen desimaalilukujen kärsiessä epätarkkuuden epäilyksistä mahdollisen mittaustarkkuuden tai pyöristämisen seurauksena.
Desimaaliluku murtoluvuksi
Desimaaliluvut voidaan muuttaa murtoluvuiksi hyödyntämällä desimaaliosan paikkojen nimityksiä kymmenesosa, sadasosa, tuhannesosa, jne. Kun luku on saatu murtolukumuotoon, se voidaan vielä supistaa yksinkertaisimpaan muotoon, joka opetellaan seuraavassa luvussa.
Esimerkki: Muuta desimaaliluku murtoluvuksi.
a) \(\mathsf{\text{0,4} = \dfrac{4}{10}}\)
b) \(\mathsf{\text{0,08} = \dfrac{8}{100}}\)
c) \(\mathsf{\text{0,52} = \dfrac{52}{100}}\)
6. Murtolukujen supistaminen ja laventaminen
Supistamisella ja laventamisella muutetaan murtoluvun osoittajaa ja nimittäjää siten, että murtoluvun arvo ei muutu. Näitä käytetään helpottamaan murtoluvun ymmärtämistä sekä vertailua muihin murtolukuihin.

Supistaminen
Supistamisessa murtoluvun osoittaja ja nimittäjä jaetaan samalla luvulla, jolloin murtoluku saadaan yksinkertaisempaan muotoon. Supistettaessa murtoluvun arvo ei muutu. Supistaja merkitään kaarella murtoluvun oikeaan yläkulmaan.
Esimerkki: Supista yksinkertaisimpaan muotoon.
Tapa 1: Kirjoitetaan välivaihe näkyviin, jotta ymmärretään, mitä supistaminen tarkoittaa.
\(\mathsf{\dfrac{12}{18}^{(\color{red}6} \!\!= \dfrac{12:\color{red}6}{18:\color{red}6} = \dfrac{2}{3}}\)
Tapa 2: Supistetaan ilman välivaihetta. Tämä on tavallisin ja yksinkertaisin tapa.
\(\mathsf{\dfrac{12}{18}^{(6} \!\!= \dfrac{2}{3}}\)
Tapa 3: Supistaa voi monta kertaa peräkkäin, jos ei heti keksi suurinta mahdollista supistajaa.
\(\mathsf{\dfrac{12}{18}^{(2} \!\!= \dfrac{6}{9}^{(3} \!\!= \dfrac{2}{3}}\)
Erilaisista laskutoimituksista vastaukseksi saatu murtoluku tulee aina supistaa yksinkertaisimpaan muotoonsa. Tämä selkeyttää vastausta.
Laventaminen
Laventamisessa murtoluvun osoittaja ja nimittäjä kerrotaan samalla luvulla. Lavennettaessa murtoluvun arvo ei muutu. Laventaja merkitään kaarella murtoluvun vasempaan yläkulmaan.
Esimerkki: Lavenna luvulla 4.
Tapa 1: Kirjoitetaan välivaihe näkyviin, jotta ymmärretään, mitä laventaminen tarkoittaa.
\(\mathsf{\rule{0pt}{1.4em}^{{\color{red}4})}\dfrac{5}{6} = \dfrac{{\color{red}4} \cdot 5}{{\color{red}4} \cdot 6} = \dfrac{20}{24}}\)
Laventamista käytetään murtolukujen yhteen- ja vähennyslaskussa, murtolukujen suuruusvertailussa sekä muutettaessa murtolukuja desimaali- tai prosenttiluvuiksi.
Samannimiset murtoluvut
Ennen murtolukujen yhteen- tai vähennyslaskua murtolukujen tulee olla samannimiset, eli niiden nimittäjien tulee olla samat.
Vinkkejä samannimiseksi laventamiseen:
- Lavenna vain toista murtolukua, jos toinen nimittäjä on toisen moninkerta.
\(\mathsf{\rule{0pt}{1.4em}^{2)}\dfrac{2}{3} - \dfrac{1}{6} = \dfrac{4}{6} - \dfrac{1}{6} = \dfrac{3}{6}^{(3} \!\!= \dfrac{1}{2}}\) - Selvitä mahdollisimman pieni luku (kts. luku 3, Pienin yhteinen jaettava), johon molemmat nimittäjät voidaan laventaa.
\(\mathsf{\rule{0pt}{1.4em}^{2)}\dfrac{2}{15} +\!\! \rule{0pt}{1.4em}^{5)}\dfrac{1}{6} = \dfrac{4}{30} + \dfrac{5}{30} = \dfrac{9}{30}^{(3} \!\!= \dfrac{3}{10}}\) - Lavenna ristiin, jos luvut ovat pienä tai mikään muu ei auta.
\(\mathsf{\rule{0pt}{1.4em}^{{\color{red}2})}\dfrac{2}{\color{blue}3} - \!\!\rule{0pt}{1.4em}^{{\color{blue}3})}\dfrac{1}{\color{red}2} = \dfrac{4}{6} - \dfrac{3}{6} = \dfrac{1}{6}}\)
7. Murtolukujen yhteen- ja vähennyslasku
Laskettaessa murtolukuja yhteen, murtolukujen tulee olla samannimiset. Yhteenlaskussa osoittaja lasketaan yhteen, mutta nimittäjät pysyvät samana. Tämä on ilmeistä, sillä laskettaessa esimerkiksi viidesosia yhteen, saadaan vastaukseksi tietenkin viidesosia.
Esimerkki: Laske.
\(\mathsf{\dfrac{2}{5} + \dfrac{1}{5} = \dfrac{3}{5}}\)
Jos murtoluvut eivät ole samannimisiä, täytyy murtoluvut laventaa ensin samannimisiksi.
Esimerkki: Laske.
\(\mathsf{\rule{0pt}{1.4em}^{2)}\dfrac{4}{5} - \dfrac{3}{10} = \dfrac{8}{10} - \dfrac{3}{10} = \dfrac{5}{10}^{(5}\!\! = \dfrac{1}{2}}\)
Algoritmi murtolukujen yhteen- ja vähennyslaskuun
- Muunna sekaluvut murtoluvuiksi, jos niitä esiintyy.
- Muunna murtoluvut tarvittaessa samannimisiksi.
- Laske lasku osoittajilla.
- Nimittäjä pysyy samana.
- Supista vastaus, jos mahdollista.
- Muuta sekaluvuksi, jos mahdollista.
8. Murtolukujen kertolasku
Murtoluvun kertominen kokonaisluvulla
Vanhastaan tiedetään, että kertolasku on lyhyempi tapa kirjoittaa toistuva yhteenlasku. Tämän perusteella voidaan johtaa laskusääntö kertolaskulle myös murtolukujen tapauksessa.
Esimerkki: Laske muuttamalla kertolasku yhteenlaskuksi.
\(\mathsf{3 \cdot \dfrac{2}{5} = \dfrac{2}{5} + \dfrac{2}{5} + \dfrac{2}{5} = \dfrac{6}{5} = 1\dfrac{1}{5}}\)
Kuten huomataan, kertolasku on kohdistunut vain osoittajaan \(\mathsf{3 \cdot 2 = 6}\), mutta nimittäjä on pysynyt samana. Murtoluvun ja kokonaisluvun kertolasku voidaan siis ajatella myös näin.
Esimerkki: Laske.
\(\mathsf{3 \cdot \dfrac{2}{5} = {\color{gray}\dfrac{3\cdot 2}{5}} = \dfrac{6}{5} = 1\dfrac{1}{5}}\)
Välivaihetta (harmaalla) ei tarvitse merkitä näkyviin, vaan kertolaskun voi suoraan laskea osoittajaan.
Osan ottaminen luvusta
Osan ottaminen luvusta tapahtuu siten, että osaa kuvaavalla murtoluvulla kerrotaan lukua, josta osaa otetaan.
Esimerkki: Kuinka paljon on \(\mathsf{\dfrac{3}{5}}\) 40 eurosta?
\(\mathsf{\dfrac{3}{5} \cdot 40 = \dfrac{3 \cdot 40}{5} = \dfrac{120}{5} = 24}\)
Vastaus: Kolme viidesosaa 40 eurosta on 24 euroa.
Murtoluvun kertominen murtoluvulla
Kahden (tai useamman) murtoluvun kertolasku lasketaan siten, että osoittajat kerrotaan keskenään, ja nimittäjät kerrotaan keskenään.
Esimerkki: Laske.
a) \(\mathsf{\dfrac{4}{3} \cdot \dfrac{5}{7} = {\color{gray}\dfrac{4 \cdot 5}{3 \cdot 7}} = \dfrac{20}{21}}\)
b) \(\mathsf{5\cdot\dfrac{6}{7} = {\color{gray}\dfrac{5}{1} \cdot \dfrac{6}{7} = \dfrac{5 \cdot 6}{1 \cdot 7}} = \dfrac{30}{7} = 4\dfrac{2}{7}}\)
Välivaiheita (harmaalla) ei tarvitse merkitä näkyviin, vaan osoittajan ja nimittäjän voi laskea suoraan. Esimerkin b-kohdassa muutettiin murtoluvun ja kokonaisluvun kertolasku kahden murtoluvun kertolaskuksi. Näin vaikeasti sitä ei tietenkään tarvise tehdä, mutta esimerkin avulla yleistettiin murtolukujen kertolaskun laskusäännön toimivan myös kokonaislukujen tapauksessa. Havainnollistetaan murtolukujen kertolaskua vielä pienen animaation avulla. Animaation saat pyörimään painamalla vasemmasta alanurkasta nuolipainiketta.
Kertolaskun supistaminen
Ennen kertolaskun laskemista kannattaa tarkistaa, voiko tulon tekijöitä supistaa. Tulon tapauksessa supistaa voidaan siis ristiin, kunhan toinen luku on osoittaja ja toinen nimittäjä. Etukäteen tehty supistus helpottaa kertolaskun laskemista, tai tekee siitä jopa tarpeettoman.
Esimerkki: Laske. Supista ennen kertolaskun laskemista.
9. Murtolukujen jakolasku
Murtoluvun jakaminen kokonaisluvulla
Murtoluvun ja luvun jakolaskussa murtoluvun nimittäjä kerrotaan jakajalla.
Esimerkki: Laske jakolasku kertomalla nimittäjää.
\(\mathsf{\dfrac{6}{7} : 3 = {\color{gray}\dfrac{6}{7 \cdot 3}} = \dfrac{6}{21}^{(3} \!\!= \dfrac{2}{7}}\)
Välivaihetta (harmaalla) ei tarvitse merkitä näkyviin, vaan laskun voi laskea suoraan. Nimittäjän kertominen toimii aina, mutta toki siinä voi käyttää järkeäkin. Jos osoittaja voidaan suoraan jakaa jakajalla, niin tällöin edellä mainittua kikkailua ei tarvitse tehdä.
Esimerkki: Laske jakolasku jakamalla osoittaja.
\(\mathsf{\dfrac{6}{7} : 3 = \color{gray}{\dfrac{6:3}{7}} \color{black}{ = \dfrac{2}{7}}}\)
Välivaihetta (harmaalla) ei tarvitse merkitä näkyviin. Muista, että osoittajan jakaminen toimii vain, jos osoittaja on jaollinen jakajalla.
Käänteisluku
Ennenkuin pääsemme varsinaiseen kahden murtoluvun jakolaskuun meidän täytyy tutustua käänteislukuun. Käänteisluku tarkoittaa käytännössä sitä, että vaihdetaan murtoluvun osoittajan ja nimittäjän paikkaa keskenään. Virallisesti käänteisluku määritellään siten, että luvun ja sen käänteisluvun tulo on 1.
Esimerkki: Määritä luvun käänteisluku. Tarkista vastaus kertomalla.
a) Luvun \(\mathsf{\dfrac{3}{7}}\) käänteisluku on \(\mathsf{\dfrac{7}{3}}\).
\(\mathsf{\dfrac{3}{7} \cdot \dfrac{7}{3} = \dfrac{21}{21} = 1}\)
b) Luvun \(\mathsf{5}\) käänteisluku on \(\mathsf{\dfrac{1}{5}}\).
\(\mathsf{5 \cdot \dfrac{1}{5} = \dfrac{5}{5} = 1}\)
Murtolukujen jakolasku
Murtolukujen jakolasku ratkaistaan muuttamalla jakolasku kertolaskuksi vaihtamalla jakaja käänteisluvukseen, ja lasketaan muodostunut kertolasku.
Esimerkki: Laske.
a) \(\mathsf{\dfrac{3}{2} : \dfrac{3}{4} = \dfrac{3}{2} \cdot \dfrac{4}{3} = \dfrac{12}{6} = 2}\)
b) \(\mathsf{\dfrac{3}{5} : \dfrac{1}{8} = \dfrac{3}{5} \cdot 8 = \dfrac{24}{5} = 4\dfrac{4}{5}}\)
c) \(\mathsf{\dfrac{9}{4} : 2 = \dfrac{9}{4} \cdot \dfrac{1}{2} = \dfrac{9}{8} = 1\dfrac{1}{8}}\)
10. Lisätietoa: Prosenttilaskenta
Prosentti on sadasosa. Prosentti on vakioitu tapa ilmoittaa suhteellinen osuus jostakin kokonaisuudesta, eli sadasta prosentista. Prosenttilukua merkitään %-merkillä. Prosenttilukua vastaavaa osuutta kutsutaan prosenttiarvoksi. Kokonaisuutta, eli 100%, kutsutaan perusarvoksi.
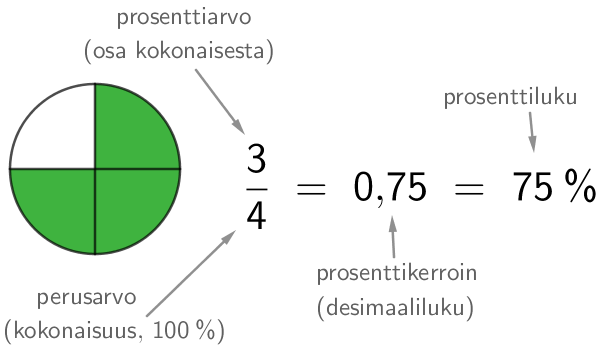
Murtoluku voidaan muuttaa prosenttiluvuksi kahdella tavalla. Murtoluku voidaan supistaa/laventaa sadasosiksi, jolloin osoittaja kertoo prosenttiluvun arvon. Toinen tapa on muuttaa murtoluku desimaaliluvuksi ja kertoa se sadalla.
Esimerkki: Muunna murtoluku prosenttiluvuksi.
a) \(\mathsf{\dfrac{55}{100} = \text{55 %}}\)
b) \(\mathsf{\rule{0pt}{1.4em}^{20)}\dfrac{3}{5} = \dfrac{60}{100} = \text{60 %}}\)
c) \(\mathsf{\dfrac{7}{8} = \text{0,875} = \text{87,5 %}}\)
Prosenttiluvun laskeminen (Kuinka monta prosenttia?)
Jonkin osan suhteellinen osuus prosentteina voidaan laskea murtolukujen kautta. Muodostetaan ensin tarkasteltavasta tilanteesta murtoluku, ja muutetaan se sitten prosenttiluvuksi.
Esimerkki: Kuinka monta prosenttia
a) luku 5 on luvusta 8
\(\mathsf{\dfrac{5}{8} = \text{0,625} = \text{62,5 %}}\)
b) 26 euroa on 65 eurosta.
\(\mathsf{\dfrac{26}{65} = \text{0,4} = \text{40 %}}\)
c) 29 torjuttua laukausta on 31 laukauksesta.
\(\mathsf{\dfrac{29}{31} = \text{0,935...} \approx \text{94 %}}\)
Prosenttiarvon laskeminen (Kuinka paljon?)
Murtolukujen kertolaskun yhteydessä opittiin ottamaan osa jostakin luvusta. Osan suuruus ilmoitettiin murtolukuna, ja osa saatiin kertolaskun avulla. Jos osan suuruus ilmoitetaankin prosenttilukuna, voidaan toimia samalla tavalla. Prosenttiluku tulee kuitenkin muuttaa ensin prosenttikertoimeksi (desimaaliluvuksi), eli jakaa sadalla.
Esimerkki:
a) Kuinka paljon on 70 % luvusta 80?
\(\textsf{70 % = 0,7}\)
\(\mathsf{\text{0,7} \cdot 80 = 56}\)
b) Kuinka paljon on 6 % 124 eurosta?
\(\textsf{6 % = 0,06}\)
\(\mathsf{\text{0,06} \cdot 124\euro = 74,40\euro}\)
c) Kuinka paljon on 94 % 640 metristä?
\(\textsf{94 % = 0,94}\)
\(\mathsf{\text{0,94} \cdot \text{640 m} = \text{601,6 m}}\)