MA7 Jakso 1: Kokonais- ja desimaaliluvut
1. Kymmenjärjestelmä
Desimaalijärjestelmä on kymmenkantainen paikkajärjestelmä, missä on käytössä siis 10 numeroa (0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9), ja numeron paikalla luvussa on merkitystä.
Luonnollisia lukuja ovat nolla ja sitä suuremmat kokonaiset luvut, joiden avulla voidaan ilmaista esimerkiksi lukumäärää. Mitä enemmän luvussa on numeroita sitä suurempi luku on. Numeroiden määrä kuvastaa siis luvun suuruusluokkaa. Suuruusluokkia ovat siis esimerkiksi ykköset, kymmenet, sadat, tuhannet, jne.
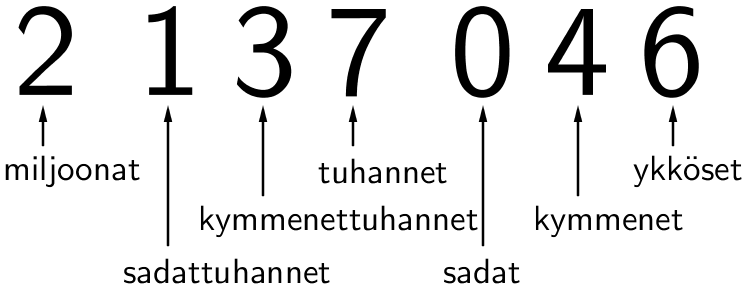
Luku voidaan ryhmitellä lukemisen selventämiseksi oikealta lähtien kolmen numeron joukoiksi. Näiden kolmen numeron joukkojen mukaisesti luvun suuruus voidaan myös kirjoittaa tai sanoa. Kyseinen luku on siis

Luvut kannattaa selkeyden vuoksi kirjoittaa erikseen, vaikka ne kieliopillisesti yhdyssanoja ovatkin. Tekstin seassa kuitenkin vältetään suurten lukujen kirjoittamista sanoin ja käytetään numeroita. Nyrkkisääntönä voidaan pitää, että kaikki lukua kymmenen suuremmat luvut kirjoitetaan numeroin.
2. Lukusuora
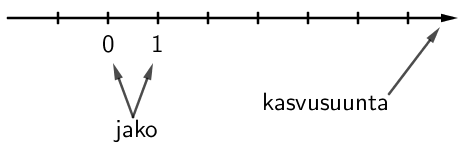
Lukusuora on viiva, johon on merkitty lukuja tai niiden paikkoja, ja joka kuvaa lukujen suuruusjärjestystä ja etäisyyttä toisistaan. Lukusuoraa käytetään havainnollistamaan lukujen paikkaa suhteessa muihin lukuihin. Lukusuora piirretään usein vaakasuoraan, mutta pystysuora lukusuora mallintaa hyvin esimerkiksi lämpömittaria.
Lukusuora kasvaa aina merkityn nuolen suuntaan. Lukusuora voidaan jakaa tarpeen mukaisiin osiin. Jako tulee merkitä näkyviin ilmoittamalla vähintään kaksi tunnettua lukua lukusuoralta. Kahden poikittaisviivan välinen etäisyys voi siis olla tarvittaessa muutakin kuin 1. Suuria lukuja verratessa tai vaikka aikajanaa piirrettäessä jako voi olla esimerkiksi 10, 100 tai 1000.
Aluksi tutustutaan lukusuoraan luonnollisilla luvuilla. Myöhemmin jakson aikana lukusuoraa laajennetaan kattamaan myös negatiiviset luvut (kokonaisluvut). Lopuksi tutustutaan kokonaisen osia kuvaaviin desimaalilukuihin.
3. Peruslaskutoimitukset
Peruslaskutoimituksia ovat
- summa (yhteenlasku)
- erotus (vähennyslasku)
- tulo (kertolasku)
- osamäärä (jakolasku)
Peruslaskutoimitusten tunteminen ja hallitseminen on tärkeätä, koska muut koulumatematiikan tiedot ja taidot perustuvat vahvasti peruslaskutoimitusten osaamiselle.
Summa ja erotus
Summa
Summa tarkoittaa joko yhteenlaskun tulosta tai yhteenlaskulauseketta. Luku joka esiintyy summassa on nimeltään summattava tai yhteenlaskettava. Yhteenlaskussa luvun suuruus kasvaa, eli lukusuoralla siirrytään oikealle (nuolen suuntaan).
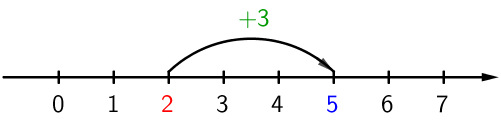
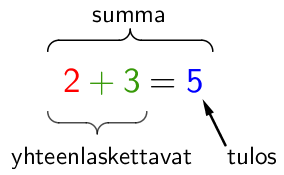
Erotus
Erotus tarkoittaa joko vähennyslaskun tulosta tai vähennyslaskulauseketta. Erotuksen ensimmäinen luku on nimeltään vähennettävä ja muut ovat vähentäjiä. Vähennyslaskussa luvun suuruus pienenee, eli siirrytään lukusuoralla vasemmalle (vastakkaiseen suuntaan kuin nuoli).

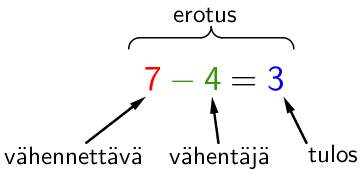
Summan ja erotuksen välinen yhteys
Jos summasta vähennetään toinen yhteenlaskettavista, niin saadaan vastaukseksi toinen yhteenlaskettava.
\(\begin{align}\mathsf{{\color{green}8} + {\color{blue}5} = {\color{red}13}}\\ \mathsf{{\color{red}13} - {\color{blue}5} = {\color{green}8}}\\ \mathsf{{\color{red}13} - {\color{green}8} = {\color{blue}5}}\end{align}\)
Tulo ja osamäärä
Tulo
Tulo tarkoittaa joko kertolaskun tulosta tai kertolaskulauseketta. Tuloon osallistuvia lukuja kutsutaan tulon tekijöiksi. Kertolasku on lyhyempi tapa ilmaista summa, jossa jotakin lukua lasketaan itsensä kanssa yhteen useita kertoja.
Esimerkki: Kirjoita kertolasku yhteenlaskuna.
a) \(\mathsf{4 \cdot 2 = 2 + 2 + 2 + 2}\)
b) \(\mathsf{3 \cdot 7 = 7 + 7 + 7}\)
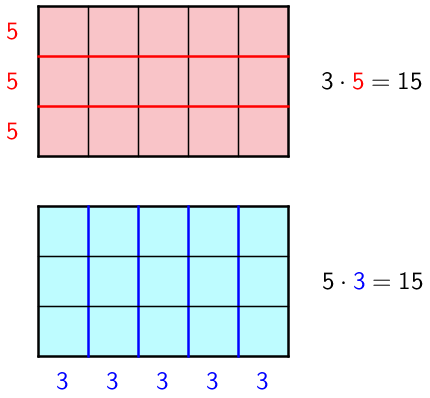
Kertolaskua on helppo havainnollistaa suorakulmion muotoisen alueen sisältämien ruutujen laskemisessa. Alla olevasta kuvasta voidaan myös havaita kertolaskun vaihdannaisuus, eli \(\mathsf{5 \cdot 3 = 3 \cdot 5 = 15}\).
Osamäärä
Osamäärä eli jakolasku on tulon vastakkainen laskutoimitus. Jakolaskua voidaan merkitä joko
- jakoviivalla \( \mathsf{\dfrac{40}{8} = 5} \)
- kaksoispisteellä \( \mathsf{40:8=5} \) tai
- kauttaviivalla \( \mathsf{40/8 = 5} \)
Osamäärän ensimmäistä (ylempää) lukua kutsutaan jaettavaksi ja jälkimmäistä jakajaksi.
Tulon ja osamäärän välinen yhteys
Jos jokin tulo jaetaan toisella tulon tekijällä, niin saadaan vastaukseksi toinen tulon tekijöistä.
\(\begin{align}&\mathsf{{\color{blue}8} \cdot {\color{green}5} = {\color{red}40}} \\ &\mathsf{\dfrac{\color{red}40}{\color{blue}8} = {\color{green}5}}\\ &\mathsf{\dfrac{\color{red}40}{\color{green}5} = {\color{blue}8}}\end{align}\)
Osittelu
Osittelun tarkoituksena on löytää menetelmiä peruslaskutoimitusten päässälaskuun. Esiteltävät merkinnät ovat enemmänkin ohjeellisia ja niiden tarkoituksena on havainnollistaa menetelmän toimintaa. Myöhemmin joitain menetelmiä käytetään apuna myös kirjainlaskennassa.
Summa
Suuret yhteenlaskettavat voidaan pilkkoa ykkösiksi, kymmeniksi, sadoiksi, jne. ja laskea helpommat yhteenlaskut keskenään. Lopuksi osasummat lasketaan vielä yhteen, jotta saadaan lopullinen vastaus.
Esimerkki: Laske.
\(\begin{align}\mathsf{1391 + 5835} &= \mathsf{{\color{red}1000} + {\color{blue}300} + {\color{green}90} + 1 + {\color{red}5000} + {\color{blue}800} + {\color{green}30} + 5} \\ &=\mathsf{{\color{red}6000} + {\color{blue}1100} + {\color{green}120} + 6}\\ &=\mathsf{7226}\end{align}\)
\(\begin{align}&\mathsf{1391 + 5835}\\ &= \mathsf{{\color{red}1000} + {\color{blue}300} + {\color{green}90} + 1}\\ &\quad +\;\mathsf{{\color{red}5000} + {\color{blue}800} + {\color{green}30} + 5} \\ &=\mathsf{{\color{red}6000} + {\color{blue}1100} + {\color{green}120} + 6}\\ &=\mathsf{7226}\end{align}\)
Erotus
Vastaavalla tavalla vähennyslaskussa vähennettävä voidaan pilkkoa pienempiin osiin, ja vähentää osat yksi kerrallaan vähennettävästä.
Esimerkki: Laske.
\(\begin{align}\mathsf{2329 - 891} &= \mathsf{2329 - {\color{red}800} - {\color{blue}90} - 1} \\&=\mathsf{1529 - {\color{blue}90} - 1}\\ &=\mathsf{1439 - 1}\\ &=\mathsf{1438}\end{align}\)
Tulo
Suurta lukua kerrottaessa luku voidaan pilkkoa suuruusluokkien (ykköset, kymmenet, sadat...) mukaisiin pienempiin osiin (summaksi), ja kertoa niitä erikseen. Lopuksi osatulokset lasketaan yhteen, jolloin saadaan lopullinen vastaus.
Esimerkki: Laske.
\(\begin{align}\mathsf{7 \cdot 497} &= \mathsf{7 \cdot ({\color{red}400} + {\color{blue}90} + {\color{green}7})}\\ &= \mathsf{7 \cdot {\color{red}400} + 7 \cdot {\color{blue}90} + 7 \cdot {\color{green}7}}\\ &=\mathsf{{\color{red}2800} + {\color{blue}630} + {\color{green}49}}\\ &=\mathsf{3479}\end{align}\)
Osamäärä
Jakolaskussa jaettava voidaan jakaa osiin (summaksi), jakaa helpommat jakolaskut erikseen, ja lopuksi laskea yhteenlasku, jolloin saadaan lopullinen vastaus.
Esimerkki: Laske.
\(\begin{align}\mathsf{\dfrac{732}{3}} &= \mathsf{\dfrac{{\color{red}600} + {\color{blue}120} + {\color{green}12}}{3}}\\ &=\mathsf{\dfrac{\color{red}600}{3} + \dfrac{\color{blue}120}{3} + \dfrac{\color{green}12}{3}}\\ &= \mathsf{{\color{red}200} + {\color{blue}40} + {\color{green}4}}\\ &= \mathsf{244}\end{align}\)
Osittelun voi tehdä alussa haluamallaan tavalla, kunhan luvut ovat sellaisia, että ne on helppoa jakaa tasan.
Lisätietoa: Allekkainlasku
Summa ja erotus allekkainlaskuna
Suuria lukuja voidaan laskea yhteen allekkainlaskun avulla. Menetelmä perustuu siihen, että lasketaan kukin suuruusluokka (ykköset, kymmenet, sadat, ...) keskenään yhteen, ja ylimenevät osat lasketaan tarvittaessa seuraavassa vaiheessa. Yhteenlaskua allekkain käytetään myös silloin kun lukuja on paljon.
Suurten lukujen erotus voidaan myös laskea allekkain. Tässäkin lähdetään ykkösistä liikkeelle ja yritetään vähentää ylemmästä numerosta alempi. Jos se ei onnistu, niin voidaan lainata suuruusluokkaa suuremmista numeroista.
Tulo ja osamäärä allekkainlaskuna
Allekkain kertolaskun idea perustuu tekijöiden jakamiseen kokonaisiin, kymmeniin, satoihin, jne., jolloin yksittäiset kertolaskut saadaan helpommiksi. Lopuksi kertolaskujen tulokset lasketaan yhteen.
Allekkain jakolaskussa jaettavaa jaetaan numero kerrallaan lähtien vasemmalta. Yksittäisistä jakolaskuista jäävä jakojäännös liitetään seuraavan numeron kymmeniksi. Allekkain jakolaskulla saadaankin kätevästi jakojäännös selville, jota tutkitaan tarkemmin seuraavassa jaksossa.
Lisätietoa: Vaihdannaisuus
Vaihdannaisuus eli kommutatiivisuus on laskutoimituksen ominaisuus, joka kuvaa mahdollisuutta vaihtaa laskutoimituksen luvut toisin päin ilman, että laskun tulos muuttuu. Yhteenlasku on vaihdannainen laskutoimitus.
\(\mathsf{{\color{red}{4} + \color{blue}3} = 7}\)
\(\mathsf{{\color{blue}{3} + \color{red}4} = 7}\)
Vähennyslasku puolestaan ei ole vaihdannainen laskutoimitus.
\(\mathsf{{\color{red}{4} - \color{blue}3} = 1}\)
\(\mathsf{{\color{blue}{3} - \color{red}4} = -1}\)
Kertolasku on vaihdannainen laskutoimitus.
\(\mathsf{{\color{red}{4} \cdot \color{blue}3} = 12}\)
\(\mathsf{{\color{blue}{3} \cdot \color{red}4} = 12}\)
Jakolasku ei ole vaihdannainen laskutoimitus.
\(\mathsf{\dfrac{\color{red}6}{\color{blue}3} = 2}\)
\(\mathsf{\dfrac{\color{blue}3}{\color{red}6} = \text{0,5}}\)
Lisätietoa: Potenssi
Potenssimerkinnän avulla voidaan lyhentää kertolaskua, missä sama luku esiintyy tulon tekijänä useamman kerran. Potenssimerkinnässä tulon tekijän oikeaan yläkulmaan kirjoitetaan luku, joka kertoo kuinka monta kertaa tekijä kertolaskussa esiintyy.
Esimerkki: Merkitse kertolasku potenssina.
a) \(\mathsf{2 \cdot 2 \cdot 2 \cdot 2 = 2^4}\)
b) \(\mathsf{6 \cdot 6 \cdot 6 = 6^3}\)
Tulon tekijää (esimerkissä luku 2) kutsutaan kantaluvuksi, ja yläkulmassa olevaa lukua (luku 4) kutsutaan eksponentiksi. Kyseinen merkintä sanottaisiin "Kaksi potenssiin neljä", "Kaksi neljänteen" tai "Kaksi korotettuna neljänteen potenssiin".
Potenssin arvoa laskettaessa potenssimerkintä voidaan kirjoittaa ensin kertolaskuna, ja laskea kertolasku normaalisti tämän jälkeen.
Esimerkki: Laske.
a) \(\mathsf{6^2 = 6 \cdot 6 = 36}\)
b) \(\mathsf{7^2= 7 \cdot 7 = 49}\)
c) \(\mathsf{(-5)^2 = -5 \cdot (-5) = 25}\)
d) \(\mathsf{3^4 = 3 \cdot 3 \cdot 3 \cdot 3 = 81}\)
Kuten yllä olevasta esimerkistä huomataan, niin kantaluku voi olla myös negatiivinen. Negatiivinen kantaluku tulee kirjoittaa sulkeiden sisään.
Laskujärjestyksen osalta potenssit lasketaan ennen kerto- ja jakolaskuja. Suluilla voidaan potenssienkin kohdalla määrätä laskujärjestystä tarpeen mukaan.
Esimerkki: Laske.
a) \(\mathsf{5 \cdot 3^2 = 5 \cdot 9 = 45}\)
b) \(\mathsf{6^2 - 11 = 36 - 11 = 35}\)
c) \(\mathsf{(-5 \cdot 2)^2 = (-10)^2 = 100}\)
d) \(\mathsf{\dfrac{4^2}{2^4} = \dfrac{16}{16} = 1}\)
Neliöjuuri
Kuten peruslaskutoimituksilla aikaisemmin havaittiin, myös potensseilla on olemassa käänteiset laskutoimitukset. Yleisesti niitä voisi kutsua juuri-laskuiksi, mutta keskitytään nyt toiseen potenssiin korottamisen käänteiseen laskutoimitukseen eli neliöjuureen.
\(\mathsf{5^2 = 25 \qquad \Rightarrow \qquad \sqrt{25} = 5}\)
Esimerkki: Laske.
a) \(\mathsf{\sqrt{16} = 4}\)
b) \(\mathsf{\sqrt{36} = 6}\)
c) \(\mathsf{\sqrt{100} = 10}\)
d) \(\mathsf{\sqrt{1} = 1}\)
Neliöjuuren merkintänä käytetään siis erityistä juuri-merkkiä \(\sqrt{\rule{1em}{0pt}\rule{0pt}{1em}}\). Merkin alla olevaa lukua kutsutaan juurrettavaksi. Neliöjuuri vastaa siis kysymykseen "Mikä luku on kerrottu itsellään, että saadaan vastaukseksi juurrettava?".
4. Laskujärjestys
Jos laskulausekkeessa esiintyy useita laskutoimituksia, tulee sopia säännöt, joiden mukaan valitaan laskutoimituksille suoritusjärjestys. Laskujärjestyksen kanssa tulee olla erityisen tarkkana laskulauseketta syötettäessä tietokoneen tai laskimen laskettavaksi. Pääsääntöisesti ne toki yleisesti sovittua laskujärjestystä noudattavat, mutta lukujen ja laskutoimitusten syöttämisessä voi tulla epäselvyyksiä välitulosten kanssa.
Laskujärjestys
Toistaiseksi ollaan opiskeltu vain peruslaskutoimituksia, joten tarkastellaan laskujärjestystä niiden osalta. Jos lausekkeen laskutoimitukset ovat samassa vaiheessa laskettavia, suoritetaan lasku oletuksena aina järjestyksessä vasemmalta oikealle. Alle on listattu peruslaskutoimitusten laskujärjestys:
- Sulkeet
- Tulo ja osamäärä (kerto- ja jakolasku)
- Summa ja erotus (yhteen- ja vähennyslasku)
Esimerkki: Laske.
a) \(\mathsf{{\color{red}5 \cdot 4} + 16 {\color{blue} - 8 : 2} = {\color{red}20} + 16 {\color{blue} - 4} = 32}\)
b) \(\mathsf{5 \cdot ({\color{red}4 + 16 - 8}) : 2 = 5 \cdot {\color{red}12} : 2 = 60 : 2 = 30} \)
Sulkeiden avulla voidaan siis lausekkeen laskujärjestystä muuttaa. Kertolaskun laskeminen ennen yhteenlaskua on luonnollista, kun muistetaan, että kertolaskuhan oli vain lyhyempi tapa merkitä tilannetta, jossa samaa lukua summataan useita kertoja.
Murtolauseke
Murtolauseke eli rationaalilauseke tarkoittaa sellaisia lausekkeita, jotka on kirjoitettu käyttäen murtolukumerkintää. Osoittajassa ja nimittäjässä voi siis yksittäisen luvun lisäksi olla lausekkeita. Laskujärjestyksen kannalta osoittajassa ja nimittäjässä olevat lausekkeet tulee laskea ensin, ja mahdollinen murtolukumerkinnän mukainen jakolasku aivan viimeiseksi.
\(\mathsf{\dfrac{4+8}{6-3} = \dfrac{12}{3} = 4}\)
Tehtävä voitaisiin kirjoittaa ilman murtolukumerkintää seuraavasti:
\(\mathsf{(4+8) : (6-3) = 12 : 3 = 4}\)
Murtolauseke siis muuttaa laskujärjestystä ilman tarvetta sulkeiden käytölle.
Esimerkki: Laske lukujen 4, 6, 7, 8 ja 10 keskiarvo.
\(\mathsf{\dfrac{4 + 6 + 7 + 8 + 10}{5} = \dfrac{35}{5} = 7}\)
5. Suuruusvertailu
Lukujen suuruutta vertaillaan erilaisten vertailumerkkien avulla. Vertailumerkin käyttö muodostaa väitteen, joka on joko totta (tosi) tai valhetta (epätosi). Esimerkiksi väite \(\mathsf{2 = 3}\) on epätosi, kun taas \(\mathsf{2 < 3}\) on tosi. Alla olevassa taulukossa on kuvattu erilaisia vertailumerkkejä esimerkkeineen.
| Merkki | Selitys | Esimerkki |
|---|---|---|
| \(\mathsf{ = }\) | Yhtä suuri kuin | \(\mathsf{1+1=2}\) |
| \(\mathsf{<}\) | Pienempi kuin | \(\mathsf{3 < 4}\) |
| \(\mathsf{>}\) | Suurempi kuin | \(\mathsf{6>5}\) |
| \(\mathsf{\leq}\) | Pienempi tai yhtä suuri kuin | \(\mathsf{x \leq 7}\) |
| \(\mathsf{\geq}\) | Suurempi tai yhtä suuri kuin | \(\mathsf{x \geq 8}\) |
| \(\mathsf{\neq}\) | Erisuuri kuin | \(\mathsf{9\neq 10}\) |
| \(\mathsf{\approx}\) | Likimain yhtä suuri kuin | \(\mathsf{10{,}8 \approx 11}\) |
Välin merkitseminen
Jos halutaan ilmaista jotakin lukujoukkoa, joka on haluttujen lukujen välissä, voidaan väli ilmaista suuruusvertailumerkkien avulla.
\(\mathsf{\text{alaraja} < x < \text{yläraja}}\)
Lisäksi yhtäsuuruuden hyväksyvillä merkeillä ≤ ja ≥ voidaan määrittää lukuväli avoimeksi tai suljetuksi. Avoimessa välissä välin päätepisteet eivät kuulu mukaan lukujoukkoon. Suljetussa välissä päätepisteet kuuluvat mukaan lukujoukkoon. Alla olevassa esimerkissä on esitetty erilaisia lukuvälejä.
Esimerkki: Mitkä luvut sopivat muuttujan x paikalle?
a) avoin väli \(\mathsf{3 < x < 5}\)
Sopivat luvut: \(\mathsf{4}\)
b) suljettu väli \(\mathsf{3 \leq x \leq 5}\)
Sopivat luvut: \(\mathsf{3, 4, 5}\)
c) vasemmalta avoin väli \(\mathsf{3 < x \leq 5}\)
Sopivat luvut: \(\mathsf{4, 5}\)
d) oikealta avoin väli \(\mathsf{3 \leq x < 5}\)
Sopivat luvut: \(\mathsf{3, 4}\)
Desimaalilukuja voidaan annetulle välille muodostaa ääretön määrä, koska desimaaliluvun tarkkuutta voidaan aina lisätä. Tämän vuoksi desimaalilukuväliä määriteltäessä kannattaa määrittää sopiville desimaaliluvuille jokin tarkkuus, esimerkiksi kaksi desimaalia tai kymmenesosien tarkkuus. Desimaalilukuja luetellessa käytetään luettelomerkkinä pilkun sijaan kaksoispistettä, jotta se ei mene desimaalipilkun kanssa sekaisin.
Esimerkki: Mitkä yksidesimaaliset luvut sopivat muuttujan x paikalle?
a) avoin väli \(\mathsf{3 < x < 4}\)

Sopivat luvut: \(\mathsf{\text{3,1}; \text{3,2}; \text{3,3}; \text{3,4}; \text{3,5}; \text{3,6}; \text{3,7}; \text{3,8}; \text{3,9}}\)
b) \(\mathsf{\text{1,23} < x < \text{1,68}}\)

Sopivat luvut: \(\mathsf{\text{1,3}; \text{1,4}; \text{1,5}; \text{1,6}}\)
Yhtäsuuruusmerkin käytöstä
Käytetyin vertailumerkki koulumatematiikassa lienee yhtäsuuruusmerkki (\(\mathsf{=}\)). Sitä käytetään mm. lausekkeen ja tuloksen välissä ilmaisemassa, että lausekkeen arvo on yhtä suuri kuin tulos.
\(\mathsf{4+5=9}\)
Toisaalta yhtäsuuruusmerkkiä käytetään myös sievennettyjen lausekkeiden välissä kuvaamaan, että kaksi lauseketta ovat yhtä suuria.
\(\mathsf{3 \cdot 4 + 5 = 12 + 5}\)
Yhtäsuuruusmerkin avulla voidaan myös kirjoittaa pidempiä väitteitä, jossa jotakin lauseketta sievennetään useita kertoja. Esimerkiksi
\(\mathsf{3 \cdot 4 + 5 = 12 + 5 = 17}\)
Selvyyden vuoksi pidemmät sievennykset kannattaa kirjoittaa useammalle riville siten, että yhtäsuuruusmerkki aloittaa uuden rivin.
\(\begin{align}&\mathsf{5 \cdot 4 + 3 \cdot (5-3)}\\=\;&\mathsf{5 \cdot 4 + 3 \cdot 2}\\=\;&\mathsf{ 20 + 6}\\=\;&\mathsf{ 26}\end{align}\)
Yhtäsuuruusmerkkiä käytetään usein myös väärin lisäämällä kesken sievennyksen uusia laskutoimituksia lausekkeeseen. Tällöin yhtäsuuruus ei enää pidä paikkaansa, eli väitteestä tulee epätosi. Alkuperäisen lausekkeen ja viimeisen sievennetyn lausekkeen (vastauksen) tulee olla yhtä suuria. Jokaisessa sievennyksen välivaiheessa tehdään siis vain laskujärjestyksen mukaisia muutoksia edelliseen lausekkeeseen eikä mitään lisätä tai jätetä pois lausekkeesta.
Esimerkki: Timo ja Pekka ostavat rautakaupasta kaksi 25 euron hintaista rautakankea sekä 40 euron hintaisen lapion. He jakavat kustannukset tasan. Kuinka paljon kullekkin tulee maksettavaa.
Oikea tapa 1: (Yksi lauseke)
\(\mathsf{\dfrac{2 \cdot 25 + 40}{2}=\dfrac{50 + 40}{2}=\dfrac{90}{2}=45}\)
Vastaus: Maksettavaa tulee 45 euroa.
Oikea tapa 2: (Kaksi lauseketta)
Kokonaishinta:
\(\mathsf{2 \cdot 25 + 40 = 50 + 40 = 90}\)
Kustannusten jakautuminen:
\(\mathsf{90 : 2 = 45}\)
Vastaus: Maksettavaa tulee 45 euroa.
Väärä tapa:
\(\begin{align}&\mathsf{2 \cdot 25 + 40}\\ =\;&\mathsf{50 + 40}\\=\;&\mathsf{90 : 2 \; \leftarrow {\color{red}\small\text{jakolasku ei voi ilmestyä kesken kaiken}}}\\=\;&\mathsf{45}\end{align}\)
Vastaus: Maksettavaa tulee 45 euroa.
6. Kokonaisluvut
Laajennetaan lukualuetta luonnollisista luvuista kokonaislukuihin, jolloin ns. positiivisten kokonaislukujen (1, 2, 3,...) ja nollan lisäksi on mukana myös negatiiviset kokonaisluvut (-1, -2, -3,...).

Kokonaisluvut lukusuoralla
Kokonaislukuja on helpompi ymmärtää lämpömittarin tai lukusuoran avulla, jonka yhteydessä negatiivisia lukuja ollaan totuttu käsittelemään. Lämpömittari onkin käytännössä sama asia kuin pystyyn nostettu lukusuora.
Tärkeätä on ymmärtää, että luvut kasvavat lukusuoralla nuolen suuntaan (oikealle), jolloin vastakkaiseen suuntaan (vasemmalle) mentäessä luvut pienenevät. Esimerkiksi luku \(\mathsf{-3}\) on siis pienempi kuin \(\mathsf{-1}\).
Vastaluku
Tarkastellaan lukusuoraa. Luvun vastaluku on yhtä kaukana nollasta kuin alkuperäinen luku, mutta vastakkaisella puolella. Vastalukua merkitään miinusmerkillä.
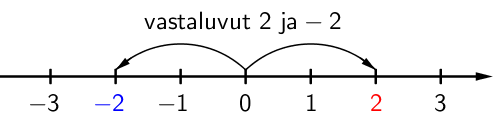
Esimerkiksi luvun \( \mathsf{2} \) vastaluku on \( \mathsf{-2} \). Eli vastaluku saadaan laittamalla luvun eteen miinusmerkki.
Toisaalta, luvun \( \mathsf{-2} \) vastaluku on \( \mathsf{2} \), eli voidaan sanoa, että luvun vastaluvun vastaluku on luku itse. Matemaattisin merkinnöin tämä näyttäisi siis seuraavalta \( \mathsf{-(-2) = 2} \). Sulkeet luvun \( \mathsf{-2} \) edessä ovat selkeyttämässä peräkkäisten miinumerkkien merkintää sekä pakollinen tyyliseikka.
Lisäksi luvulla ja sen vastaluvulla on sellainen ominaisuus, että niiden summa on aina 0. Tätä tietoa käytetään hyväksi mm. lukio-opinnoissa, kun osoitetaan kahden luvun olevan toistensa vastalukuja. Tällöin on toki yleensä käytössä kokonaislukujakin monimutkaisemmat lukujoukot.
Itseisarvo
Luvun etäisyyttä nollasta kutsutaan luvun itseisarvoksi. Itseisarvoa merkitään kahdella pystyviivalla luvun ympärillä. Koska itseisarvo kuvaa etäisyyttä jostakin, se on aina etumerkitön, eli positiivinen luku.
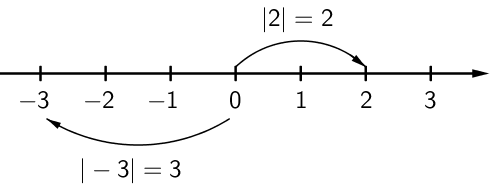
Erotuksen itseisarvo
Erotuksella saadaan nimensä mukaisesti selville kahden asian (luku, pituus, paino, rahamäärä, ...) välinen suuruusero. Suuruuseron tulisi olla aina positiivinen luku, mutta erotusta laskiessa vastaus voi olla myös negatiivinen luku, kun pienemmästä luvusta vähennetään suurempi.
Esimerkiksi tietokoneella laskettaessa olisi kätevää määritellä suuruuseron laskeminen siten, että lukujen järjestyksellä ei ole väliä, ja vastaus olisi aina positiivinen. Tähän ongelmaan käytetään erotuksen itseisarvoa, jolloin saadaan mahdollinen miinusmerkki pois luvun edestä.
Esimerkki: Laske lukujen
a) \(\mathsf{4}\) ja \(\mathsf{7}\) suuruusero.
\(\mathsf{|4-7| = |-3| = 3}\)
b) \(\mathsf{-4}\) ja \(\mathsf{7}\) suuruusero.
\(\mathsf{\left|-4-7\right| = |-11| = 11}\)
c) \(\mathsf{4}\) ja \(\mathsf{-7}\) suuruusero.
\(\mathsf{\left|\:4-(-7)\right| = |4+7| = |11| = 11}\)
d) \(\mathsf{-4}\) ja \(\mathsf{-7}\) suuruusero.
\(\mathsf{\left|-4-(-7)\right| = |-4+7| = |3| = 3}\)
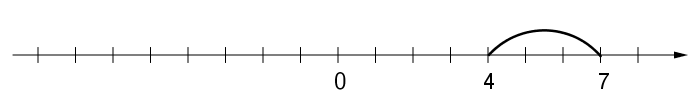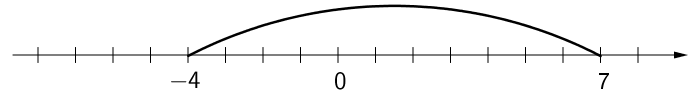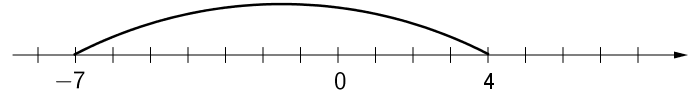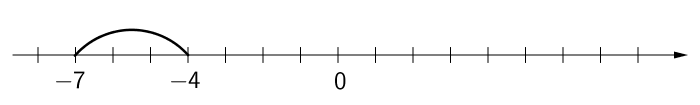
7. Kokonaislukujen summa ja erotus
Kokonaislukujen summa ja erotus
Kokonaislukujen summan ja erotuksen eli yhteen- ja vähennyslaskun laskemista voidaan helpottaa lämpömittarin avulla. Esimerkiksi laskutoimitus
\( \mathsf{-3 + 7 = 4} \)
voidaan ajatella, että lämpötila on aluksi \( \mathsf{-3\;^\circ\text{C}} \) ja se nousee tämän jälkeen \( \mathsf{7\;^\circ \text{C}} \). Uusi lämpötila on \( \mathsf{4\;^\circ \text{C}}\).
Vastaavasti vähennyslaskussa
\( \mathsf{3 - 12 = -9} \)
lämpötila voidaan ajatella olevan aluksi \( \mathsf{3\;^\circ \text{C}} \) ja tämän jälkeen se laskee \( \mathsf{12\;^\circ \text{C}} \). Uusi lämpötila on siis \( \mathsf{-9\;^\circ \text{C}} \).
Merkkien sieventäminen
Koska miinusmerkki on saanut nyt uuden merkityksen, tulee jatkossa osata sieventää useita perättäisiä etumerkkejä. Sievennyssäännöt ovat seuraavat.

Käytännössä tällaisia tilanteita tulee vastaan kokonaislukujen yhteen- ja vähennyslaskujen kohdalla. Varsinkin jaksossa 3 (kirjainlaskenta) tulee merkkien sievennyssäännöt olla hyvin muistissa, kun muuttujalausekkeeseen sijoitetaan kokonaislukuja. Vastaavasti 8. luokalla potenssien laskusääntöjen yhteydessä kerrataan merkkisääntöjä, kun negatiivisia lukuja korotetaan potenssiin. Tätä varten on hyvä ymmärtää, että pariton määrä miinusmerkkejä sievenee miinukseksi ja parillinen määrä plussaksi.
Esimerkki: Sievennä.
a) \( \mathsf{+(+8) = 8}\)
b) \(\mathsf{+(-6)= -6} \)
a) \( \mathsf{-(+9) = -9}\)
b) \(\mathsf{-(-4)= 4} \)
Perättäisten + ja - merkkien sieventäminen yhteen- ja vähennyslaskussa
Erilaiset laskukaavat ja tietokoneohjelmat eivät välttämättä lähtökohtaisesti tiedä ovatko luvut joita sille syötetään positiivisia vai negatiivisia. Näin ollen voidaan tulla tilanteeseen, missä yritetään esimerkiksi laskea yhteen positiivista ja negatiivista lukua. Ennenkuin tällainen lasku voidaan laskea, on sievennettävä perättäiset merkit yhdeksi aiemmin opittujen sievennyssääntöjen avulla.
Esimerkki: Sievennä ja laske.
a) \(\mathsf{{\color{red}8}+({\color{blue}-4}) = {\color{red}8 \color{blue}-4} = 4}\)
b) \(\mathsf{{\color{blue}-9} - ({\color{blue}-4}) = {\color{blue}-9 \color{red}+4} = -5}\)
Välimerkistä etumerkiksi
Toinen tapa, jolla kokonaislukujen yhteen- ja vähennyslaskua voidaan joissain tilanteissa helpottaa, on vaihtaa lukujen järjestystä. Tämä vaatii ajatusmaailman muuttamista + ja - merkkien roolista. Tähän asti on totuttu, että merkit esiintyvät kahden luvun välissä ilmaisemassa yhteen- tai vähennyslaskua. Nyt ollaan todettu, että kyseessä onkin etumerkki eikä välimerkki, joten pidetään merkki kiinni sen jäljessä tulevassa luvussa. Nyt voidaan lukujen järjestystä laskussa vaihtaa esimerkiksi näin
\(\mathsf{{\color{blue}-5 \color{red}+ 8} = {\color{red}+ 8 \color{blue}-5} = 3}\)
tai näin
\(\mathsf{{\color{red}7 \color{blue}-2 \color{blue}-5 \color{red}+4} = {\color{red}7 \color{red}+4 \color{blue}-2 \color{blue}-5} = {\color{red}11 \color{blue}-7} = 4}\)
8. Kokonaislukujen tulo ja osamäärä
Kokonaislukujen kerto- ja jakolaskussa pätevät samat merkkien sievennyssäännöt kuin aikaisemminkin. Kerto- ja jakolaskussa merkit eivät ole perättäisiä vaan nyt tutkitaan laskutoimitukseen osallistuvien lukujen etumerkkiä.
Esimerkki: Laske.
a) \(\mathsf{{\color{red}3} \cdot {\color{red}8} = {\color{red}24}}\)
b) \(\mathsf{{\color{red}3} \cdot ({\color{blue}-8}) = {\color{blue}-24}}\)
c) \(\mathsf{{\color{blue}-3} \cdot {\color{red}8} = {\color{blue}-24}}\)
d) \(\mathsf{{\color{blue}-3} \cdot ({\color{blue}-8}) = {\color{red}24}}\)
Esimerkki: Laske.
a) \(\mathsf{\dfrac{\color{red}32}{\color{red}8} = {\color{red}4}}\)
b) \(\mathsf{\dfrac{\color{red}32}{\color{blue}-8} = {\color{blue}-4}}\)
c) \(\mathsf{\dfrac{\color{blue}-32}{\color{red}8} = {\color{blue}-4}}\)
d) \(\mathsf{\dfrac{\color{blue}-32}{\color{blue}-8} = {\color{red}4}}\)
9. Desimaaliluvut
Desimaaliluvulla kuvataan niitä lukuja, joissa on kokonaisten lisäksi myös kokonaisen osia. Desimaaliosa erotetaan kokonaisosasta pilkulla. Paikkojen nimeäminen perustuu samaan logiikkaan kuin kokonaisillakin luvuilla.

Pilkun vasemmalla puolella on siis kokonaisosa, joka koostuu tuttuun tapaan ykkösistä, kymmenistä, sadoista, tuhansista jne.
Pilkun oikealla puolella desimaaliosa alkaa vasemmalta luettuna kymmenesosista, sadasosista, tuhannesosista jne.
Desimaaliluvut lukusuoralla
Lukusuoralla desimaalilukuja käytetään kokonaisten välissä kuvaamaan kymmenesosien, sadasosien, jne. avulla kokonaisten osia. Desimaalilukuja on loputtomasti, jokaisen desimaaliluvun välistä voidaan aina löytää uusi desimaaliluku.
Murtolukujen muuntaminen desimaaliluvuiksi
Murtoluvut, joissa on nimittäjänä jokin kymmenen moninkerta, vastaavat suoraan desimaalilukuja.
Esimerkki: Muuta murtoluku desimaaliluvuksi.
a) \(\mathsf{\dfrac{8}{10} = 0{,}8}\)
b) \(\mathsf{\dfrac{5}{100} = 0{,}05}\)
c) \(\mathsf{\dfrac{34}{100} = 0{,}34}\)
d) \(\mathsf{\dfrac{93}{1000} = 0{,}093}\)
Jos murtoluvun nimittäjä ei ole kymmenen moninkerta, se voidaan yrittää laventaa johonkin niistä.
Esimerkki: Muuta murtoluku desimaaliluvuksi.
a) \(\mathsf{\rule{0pt}{1.4em}^{2)}\dfrac{3}{5} = \dfrac{6}{10} = 0{,}6}\)
b) \(\mathsf{\rule{0pt}{1.4em}^{25)}\dfrac{1}{4} = \dfrac{25}{100} = 0{,}25}\)
c) \(\mathsf{\rule{0pt}{1.4em}^{5)}\dfrac{1}{20} = \dfrac{5}{100} = 0{,}05}\)
Lisätietoa: Päättymättömät desimaaliluvut
Desimaaliluku voi jatkua loputtomasti. Tällöin desimaaliluvusta kirjoitetaan vain muutama ensimmäinen desimaali, ja luvun loppuun lisätään kolme pistettä kuvaamaan desimaaliluvun jatkumista kirjoitettujen numeroiden jälkeen. Tällaisia desimaalilukuja voi tulla esimerkiksi jakolaskun vastauksena.
\(\mathsf{\dfrac{1}{3} = \text{0,3333...}}\)
Desimaaliluku voi toistaa samaa numeroa (kuten yllä) tai jotakin numerosarjaa. Tällöin sanotaan, että desimaaliluku on päättymätön jaksollinen desimaaliluku. Tällaiset luvut voidaan esittää murtolukuna. Toistuvan jakson päälle voidaan tällöin kirjoittaa viiva, joka kertoo mitkä numerot luvussa toistuvat.
Esimerkki: Laske ja merkitse päättymättömänä desimaalilukuna.
a) \(\mathsf{\dfrac{7}{11} = \text{0,63636363...} = \text{0,}\overline{63}}\)
b) \(\mathsf{\dfrac{5}{12} = \text{0,416666...} = \text{0,41}\overline{6}}\)
Desimaaliluku voi olla myös päättymätön jaksoton desimaaliluku (ns. irrationaaliluku). Näitä desimaalilukuja ei voi esittää jakolaskuna (murtolukuna) vaan niitä esiintyy esimerkiksi neliöjuurien, trigonometristen funktioiden ja luonnonvakioiden yhteydessä.
Esimerkki: Laske.
a) \(\mathsf{\sqrt{2} = \text{1,414213...}}\)
b) \(\mathsf{\text{sin}(45^\circ) = \text{0,707106...}}\)
c) \(\mathsf{\pi = \text{3,14159265...}}\)
Näihin pääset tutustumaan tarkemmin 8. ja 9. luokalla.
Desimaalierottimesta
Useissa maissa desimaalierottimena käytetään Suomen tapaan pilkkua, mutta esimerkiksi Yhdysvalloissa desimaalierottimena käytetään pistettä. Tähän törmäät varmasti käyttäessäsi laskinta tai tietokonetta. Hämäävästi pilkulla erotellaan näissä maissa tuhannet, miljoonat, miljardit jne. toisistaan. Jotta sekaannusta ei pääse sattumaan, kannattaa aina laskuja laskimella laskiessasi varmistaa käytetty merkintätapa, ja pohtia jo etukäteen vastauksen suuruusluokkaa.
10. Desimaalilukujen summa ja erotus
Desimaalilukuja voidaan laskea yhteen ja vähentää toisistaan aivan kuten kokonaisiakin lukuja.
Allekkainlasku
Lukuja allekkain asetellessa tulee varmistua, että pilkut ovat samalla kohdalla. Tällöin myös ykköset, kymmenet, kymmenesosat yms. ovat vastaavasti samalla kohtaa ja laskutoimitus onnistuu.
Esimerkki: Laske lukujen \(\textsf{5,04}\) ja \(\textsf{3,88}\) summa ja erotus allekkain.
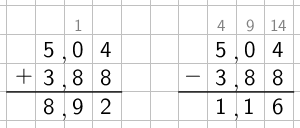
Jos desimaaliluvuissa on eri määrä desimaaleja, voidaan toiseen lisätä puuttuvien desimaalien paikalle kirjoittaa nollia, jotta allekkainlasku selkeytyy.
Päässälasku
Myös päässälaskiessa kannattaa ennen laskemista lisätä nollia desimaaliosan loppuun, mikäli luvuissa on eri määrä desimaaleja. Tämä helpottaa hahmottamaan paremmin lukujen desimaaliosan suuruutta ja suhdetta toisiinsa.
Esimerkki: Laske.
\(\textsf{7,5 + 2,34 = 7,50 + 2,34 = 9,84}\)
Toinen päässälaskua helpottava ajatusmalli on laskea kokonaisosa ja desimaaliosa erikseen, ja yhdistää ne sitten lopuksi. Esimerkiksi
Esimerkki: Laske.
\(\begin{align}&\mathsf{{\color{red}27}{,}{\color{blue}54} + {\color{red}51}{,}{\color{blue}62}}\\&=\mathsf{{\color{red}27 + 51} + {\color{blue}0{,}54 + 0{,}62}}\\&=\mathsf{{\color{red}78} + {\color{red}1}{,}{\color{blue}16}}\\&=\mathsf{{\color{red}79}{,}{\color{blue}16}}\end{align}\)
11. Desimaalilukujen tulo ja osamäärä
Desimaalilukuja kerrotaan ja jaetaan keskenään usein esimerkiksi geometriassa, kun lasketaan pituuksia, pinta-aloja tai tilavuuksia. Yksikkömuunnoksia ja prosenttilaskuja laskettaessa päädytään usein kertomaan tai jakamaan kymmenen moninkerroilla (10, 100, 1000, ...). Tarkastellaan näitä kahta tapausta tarkemmin.
Desimaalilukujen kertominen ja jakaminen kymmenen moninkerroilla
Kymmenen moninkerroilla kerrottaessa desimaaliluvussa pilkku siirtyy oikealle nollien osoittaman määrän verran.
Esimerkki: Laske.
a) \(\mathsf{3{,}14 \cdot 10 = 31{,}4}\)
b) \(\mathsf{3{,}14 \cdot 100 = 314}\)
c) \(\mathsf{3{,}14 \cdot 1000 = 3140} \)
Jos numerot, joiden yli pilkkua voidaan siirtää, loppuvat kesken, lisätään tarvittaessa luvun loppuun nollia.
Jaettaessa kymmenen moninkerroilla pilkku siirtyy puolestaan vasemmalle. Tällöin saattaa ilmetä tarve lisätä nollia luvun eteen pilkun siirtämisen mahdollistamiseksi.
Esimerkki: Laske.
a) \(\mathsf{78{,}3 : 10 = 7{,}83}\)
b) \(\mathsf{78{,}3 : 100 = 0{,}783}\)
c) \(\mathsf{78{,}3:1000 = 0{,}0783} \)
Desimaalilukujen kerto- ja jakolasku allekkain
Tärkeimmät huomionarvoiset seikat myös päässälaskun kannalta, jotka liittyvät desimaalilukujen kerto- ja jakolaskuun nähdään hyvin, kun tarkastellaan laskemista allekkain.
Alla olevassa animaatiossa tarkastellaan desimaalilukujen kertolaskua allekkain. Nyt pilkkujen ei tarvitse olla päällekkäin, vaan lopputuloksen desimaalien lukumäärä määräytyy lähtöarvojen desimaalien mukaan.
Alla olevassa animaatiossa tarkastellaan puolestaan desimaalilukujen jakolaskua allekkain. Jos jakaja on myös desimaaliluku, niin pilkusta päästään eroon siirtämällä pilkkua molemmista luvuista yhtä monta kertaa oikealle, kunnes jakaja on kokonaisluku.
Desimaalilukujen kerto- ja jakolasku päässälaskuna
Tietyissä tapauksissa desimaalilukujen kerto- ja jakolaskuja voidaan laskea helposti myös päässälaskuna. Tällöin tulee olla lähinnä tarkkana pilkun paikasta vastauksessa, johon voidaan käyttää allekkainlaskusta opittua taktiikkaa. Kertolasku voidaan laskea aluksi välittämättä pilkusta ja lopuksi lisätä pilkku oikeaan paikkaan. Oikea paikka määräytyy lähtöarvojen desimaalien lukumäärän mukaan.
Esimerkki: Laske.
a) \(\mathsf{6 \cdot \text{0,3} = \text{1,8}}\)
b) \(\mathsf{2 \cdot \text{0,3} = \text{0,6}}\)
c) \(\mathsf{\text{0,6} \cdot \text{0,3} = \text{0,18}}\)
d) \(\mathsf{\text{0,2} \cdot \text{0,3} = \text{0,06}}\)
Jakolaskussa voidaan käyttää samaa taktiikkaa kuin allekkainlaskun tapauksessa. Jos jakajassa on desimaaliluku, jakolaskua (murtolukua) kannattaa laventaa siten, että jakajana on kokonaisluku. Tämän avulla voidaan hahmottaa jakolaskua paremmin ja pilkku tulee varmemmin oikeaan paikkaan.
Esimerkki: Laske.
a) \(\mathsf{\rule{0pt}{1.5em}^{10)}\!\dfrac{12}{\text{0,3}} = \dfrac{120}{3} = 40}\)
b) \(\mathsf{\rule{0pt}{1.5em}^{10)}\!\dfrac{\text{4,2}}{\text{0,6}} = \dfrac{42}{6} = 7}\)
c) \(\mathsf{\rule{0pt}{1.5em}^{10)}\!\dfrac{\text{0,24}}{\text{0,2}} = \dfrac{\text{2,4}}{2} = \text{1,2}}\)
d) \(\mathsf{\rule{0pt}{1.5em}^{100)}\!\dfrac{1}{\text{0,05}} = \dfrac{100}{5} = 20}\)