MA9 Jakso 3: Avaruusgeometria
1. Kertausta
Pituusyksiköt
Pituuden perusyksikkö on metri, ja se lyhennetään pienellä \(\textsf{m}\)-kirjaimella. Pienempiä ja suurempia pituusyksiköitä saadaan kertomalla tai jakamalla luvulla 10, ja käyttämällä määrättyjä etuliitteitä, kuten milli-, sentti- tai kilo. Perusyksikköä metri lähimmät pituusyksiköt lyhenteineen on esitetty alla olevassa taulukossa.
| km | hm | dam | m | dm | cm | mm |
|---|---|---|---|---|---|---|
| kilometri | hehtometri | dekametri | metri | desimetri | senttimetri | millimetri |
| 1000 m | 100 m | 10 m | 1 m | 0,1 m | 0,01 m | 0,001 m |
Pinta-alayksiköt
Pinta-alan perusyksikkö on neliömetri, ja se lyhennetään merkinnällä \(\mathsf{m^2}\). Neliömetri syntyy, kun lasketaan neliön pinta-ala, jonka sivun pituus on yksi metri (\(\mathsf{1\;m \cdot 1\;m = 1\;m^2}\)). Vastaavasti neliösenttimetri saadaan kun lasketaan nelilön neliön pinta-ala, jonka sivun pituus on yksi senttimetri (\(\mathsf{1\;cm \cdot 1\;cm = 1\;cm^2}\)).
Pienempiä ja suurempia pinta-alayksiköitä saadaan siis kertomalla tai jakamalla luvulla 100, ja käyttämällä määrättyjä etuliitteitä, kuten pituusyksiköissä. Poikkeuksena on neliöhehtometri eli hehtaari sekä neliödekametri eli aari. Tärkeimmät pinta-alayksiköt lyhenteineen on esitetty alla olevassa taulukossa.
| km2 | ha | a | m2 | dm2 | cm2 | mm2 |
|---|---|---|---|---|---|---|
| neliökilometri | hehtaari | aari | neliömetri | neliödesimetri | neliösenttimetri | neliömillimetri |
| 1 000 000 m2 | 10 000 m2 | 100 m2 | 1 m2 | 0,01 m2 | 0,0001 m2 | 0,000001 m2 |
Erilaisten tasokuvioiden piirejä ja pinta-aloja
Kolmio
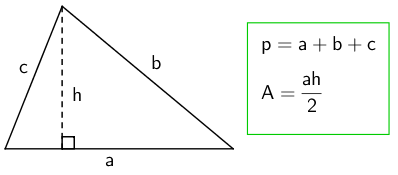
Suorakulmio
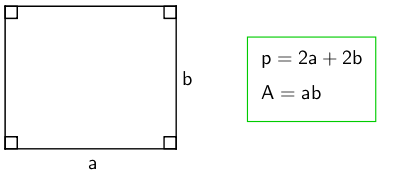
Suunnikas
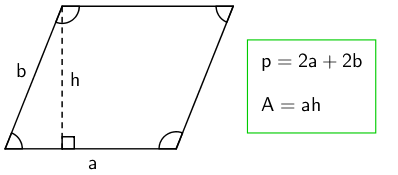
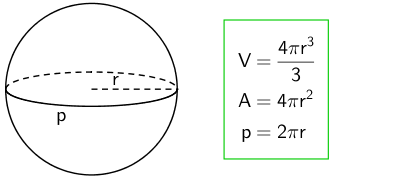
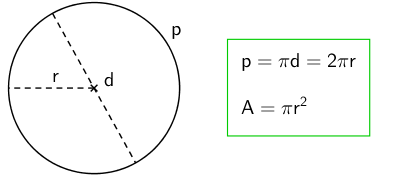
Ympyrä
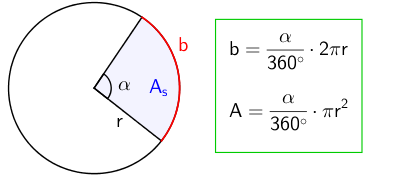
Sektori
2. Tilavuusyksiköt
Tilavuus kuvaa kolmiulotteisen kappaleen suuruutta. Kappaleiden viemän tilan lisäksi tilavuutta käytetään kuvaamaan astioiden vetoisuutta, eli sitä, kuinka paljon astiaan mahtuu esimerkiksi nestettä tai jotakin hienojakoista ainetta.
Tilavuusyksiköt
Tilavuuden perusyksikkö on kuutiometri, ja se lyhennetään merkinnällä \(\mathsf{m^3}\). Kuutiometri syntyy, kun lasketaan pinta-ala kuutiolle, jonka sivun pituus on yksi metri (\(\mathsf{1\;m \cdot 1\;m \cdot 1\;m}\)). Pienempiä ja suurempia tilavuusyksiköitä saadaan kertomalla tai jakamalla luvulla 1000, ja käyttämällä määrättyjä etuliitteitä, kuten pituusyksiköissä. Tärkeimmät tilavuusyksiköt lyhenteineen on esitetty alla olevissa taulukoissa.
| km3 | hm3 | dam3 | m3 |
|---|---|---|---|
| kuutiokilometri | kuutiohehtometri | kuutiodekametri | kuutiometri |
| 1 000 000 000 m3 | 1 000 000 m3 | 1 000 m3 | 1 m3 |
| m3 | dm3 | cm3 | mm3 |
|---|---|---|---|
| kuutiometri | kuutiodesimetri | kuutiosenttimetri | kuutiomillimetri |
| 1 m3 | 0,001 m3 | 0,000001 m3 | 0,000000001 m3 |
Vetomitat
Kuutiometrin ja sen kerrannaisten lisäksi tilavuutta voidaan mitata litroissa. Litra lyhennetään joko pienenä (l) tai isona L-kirjaimena (L). Käsin kirjoittaessa voidaan sekaannuksen välttämiseksi käyttää myös kaunokirjoitettua \(\ell\)-kirjainta (pieni L-kirjain). Litroja voidaan muuttaa kuten pituusyksiköitä pienempiin ja suurempiin kerrannaisiin kertomalla ja jakamalla luvulla 10. Litroissa käytetään samoja etuliitteitä kuin muissakin SI-järjestelmän yksiköissä, esimerkiksi desilitra (dl, dL), senttilitra (cl, cL) tai millilitra (ml, mL). Edellä mainitut ovat yleisimmin käytössä olevat vetomitat, eikä esimerkiksi kilolitroista (kl, kL) puhuta, vaikka se periaattessa mahdollinen yksikkö olisikin.
Litra on määritelty siten, että se vastaa tilavuudeltaan yhtä kuutiodesimetriä.
\(\mathsf{1\;l = 1\;dm^3}\)
Kuutiodesimetrin (dm3) tuhannesosa on kuutiosenttimetri (cm3) ja litran tuhannesosa on millilitra, joten yksi millilitra vastaa yhtä kuutiosenttimetriä
\(\mathsf{1\;ml = 1\;cm^3}\)
Muutoin vetomitat lähinnä tarkentavat tilavuusyksiköitä ja näin ollen helpottavat mittaamista.
| dm3 | cm3 | ||
|---|---|---|---|
| l | dl | cl | ml |
| litra | desilitra | senttilitra | millilitra |
| 1 l | 10 dl | 100 cl | 1000 ml |
3. Avaruuskappaleita
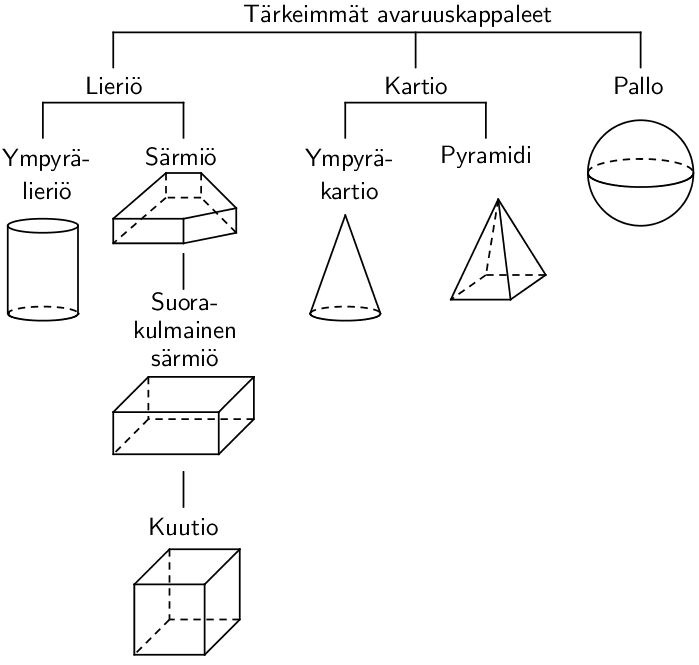
Kolmiulotteinen kappale voi olla minkä muotoinen tahansa, mutta matematiikan kannalta yksinkertaisimpia ovat lieriö, kartio ja pallo. Kaikki pallot ovat keskenään yhdenmuotoisia, vain pallon koko (säde) muuttuu. Lieriöitä ja kartioita voidaan luokitella tarkemmin niiden pohjan muodon mukaan (yleensä monikulmio tai ympyrä), ja pohjan muoto vaikuttaakin merkittävästi esimerkiksi kappaleen pinta-alan tai tilavuuden laskemiseen.
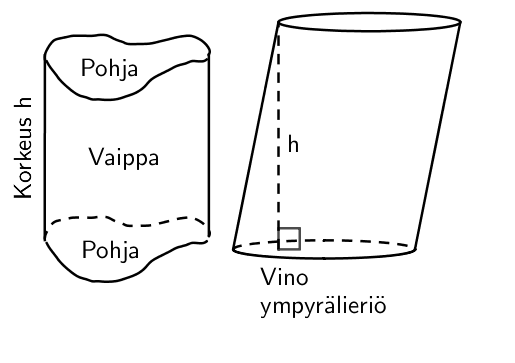
Lieriö
Lieriöllä on kaksi yhtenevää ja yhdenmuotoista pohjaa sekä niiden välissä oleva vaippa. Pohjien välistä etäisyyttä kutsutaan lieriön korkeudeksi. Suorassa lieriössä pohjat ovat samalla kohtaa, muutoin lieriö on vino.
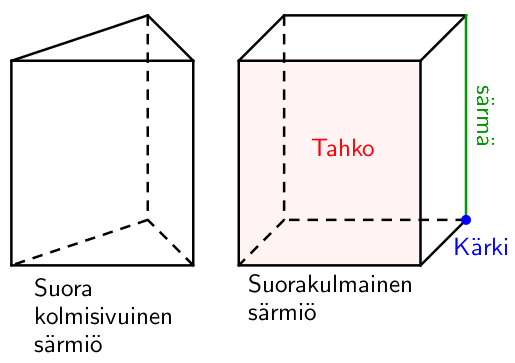
Kartio
Kartiolla on yksi pohja, josta lähtevä vaippa kapenee tasaisesti kohti huippua. Huipun ja pohjan välistä kohtisuoraa etäisyyttä kutsutaan kartion korkeudeksi. Kartio voi myös olla suora tai vino.

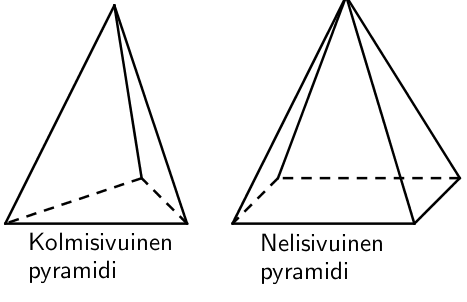
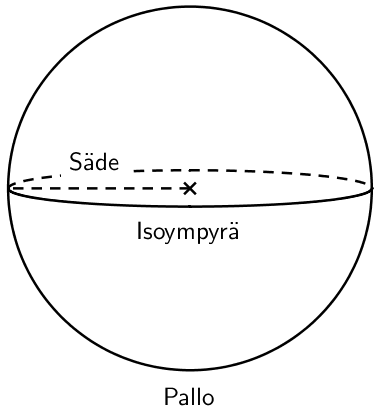
Pallo
Pallo on kappale, jonka pisteet ovat säteen r etäisyydellä keskipisteestä. Kun pallo halkaistaa kahteen yhtä suureen osaan, muodostuvaa leikkauspintaa kutsutaan isoympyräksi. Isoympyrän kehän pituus on yhtä suuri kuin pallon ympärysmitta. Esimerkiksi maapallolla tätä ympärysmittaa kutsutaan päiväntasaajaksi.
Kappaleiden piirtäminen
Kun kolmiulotteisia kappaleita piirretään kaksiulotteiselle paperille täytyy aina tehdä päätös miten syvyysvaikutelma luodaan. Taiteen ja tieteen tarkoituksia varten on luotu useita erilaisia perspektiivejä ja projektioita. Matematiikan käyttötarkoitusta palvelee parhaiten ns. yhdensuuntaisprojektiot, joista helpoin on kavaljeeriprojektio.
Suorakulmainen särmiö kavaljeeriprojektiolla
Kavaljeeriprojektiossa kolmiulotteisen kappaleen syvyysvaikutus saadaan piirtämällä syvyyteen piirrettävät viivat 45 asteen kulmassa etutasoon nähden ja jakamalla pituudet kahdella. Yksinkertaisin kappale kavaljeeriprojektion avulla piirrettäväksi on suorakulmainen särmiö.
Ympyrälieriön piirtäminen
Ympyrälieriössä syvyysvaikutelma saadaan siten, että ympyrän muotoiset pohjat piirretään soikioina eli matemaattisemmin ilmaistuna ellipsinä. Ellipsin leveys eli pohjaympyrän säde mitataan tarkasti , mutta ellipsin "pulleuden" voi piirtäjä valita vapaasti. Mitä pulleampi ellipsi, sitä ylempää kappaletta katsotaan.
4. Lieriö
Ennen 9. luokkaa geometriassa on opittu mittaamaan ja laskemaan viivojen pituuksia (1 ulottuvuus) sekä tasokuvioiden pinta-aloja (2 ulottuvuutta). Avaruusgeometriassa opitaan laskemaan myös kolmiulotteisten kappaleiden tilavuuksia sekä niiden pinta-aloja. Näin ollaan tultu käsitelleeksi kaikki tärkeimmät kuvioiden ja kappaleiden suuruutta koskevat mitat. Fysiikan opinnot laajentavat tätä vielä esimerkiksi massan, tiheyden ja tilavuuden kuvaamiseen sekä niiden keskinäiseen vertailuun.
Lieriö yleisesti
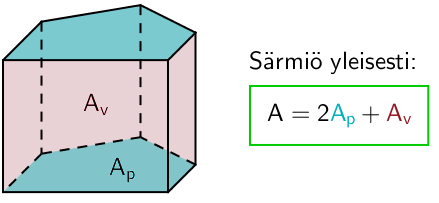
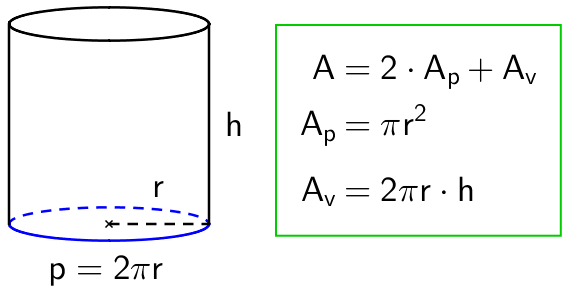
Lieriön tilavuus lasketaan kertomalla lieriön pohjan pinta-ala \(\mathsf{A_p}\) lieriön korkeudella \(\mathsf{h}\). Tämä pätee niin suoralle kuin vinollekkin lieriölle.

Lieriön pinta-ala saadaan kun kaikki pinnat lasketaan yhteen. Lieriön pinta koostuu kahdesta pohjasta \(\mathsf{A_p}\) sekä vaipasta \(\mathsf{A_v}\). Tarkempiin laskukaavoihin tutustutaan erilaisten kappaleiden yhteydessä seuraavissa luvuissa.

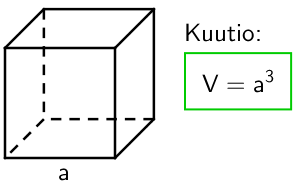
Särmiö
Tilavuus
Särmiön pohja on monikulmio. Pohjan muodosta riippuen käytetään joko lieriön tilavuuden yleistä muotoa tai suorakulmaiselle särmiölle ja kuutiolle hieman pidemmälle johdettua laskukaavaa.
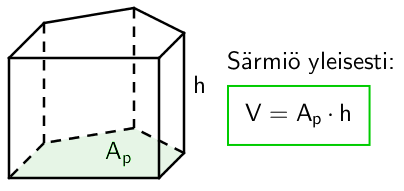

Pinta-ala
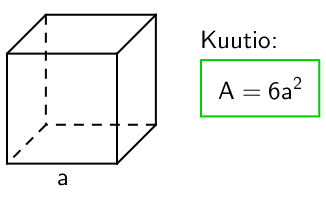
Suoran särmiön vaippa koostuu suorakulmion muotoisista tahkoista, joiden lukumäärä määräytyy pohjamonikulmion sivujen lukumäärän mukaisesti. Vinolla särmiöllä osa tahkoista on suunnikkaan muotoisia. Vaipan pinta-alaa laskettaessa tulee tahkojen pinta-alat selvittää tapauskohtaisesti erikseen, eikä mitään yleispätevää laskukaavaa kannata antaa kuin suorakulmaiselle särmiölle ja kuutiolle.

Ympyrälieriö
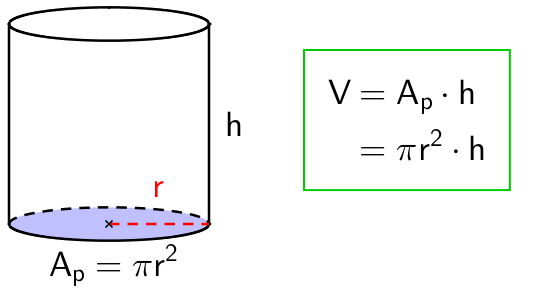
Tilavuus
Ympyrälieriön pohja on nimensä mukaisesti ympyrä.
Pinta-ala
Suoran ympyrälieriön vaippa on tasoon levitettynä suorakulmion muotoinen. Suorakulmion korkeus on sama kuin lieriön korkeus. Suorakulmion leveys on sama kuin pohjaympyrän kehän pituus.
5. Kartio
Lieriön kasvaessa pohjasta tasaisesti ylöspäin, kartio kapenee pohjasta kohti huippua. Arkielämän kartioita ovat esimerkiksi jäätelövohvelit, pyramidit sekä erilaiset suppilot. Juomalasissa, vaaseissa ja muissa kulhoissa ja kipoissa tavataan usein katkaistuja kartioita.
Kartio yleisesti
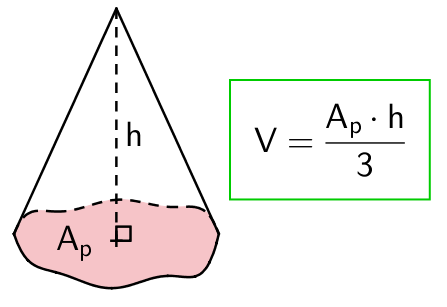
Kartion tilavuus on kolmasosa lieriöstä, jolla on sama pohjan pinta-ala ja korkeus. Kartio voi olla suora tai vino.
Kartion pinta-ala koostuu pohjan pinta-alasta \(\mathsf{A_p}\) ja vaipan pinta-alasta \(\mathsf{A_v}\).
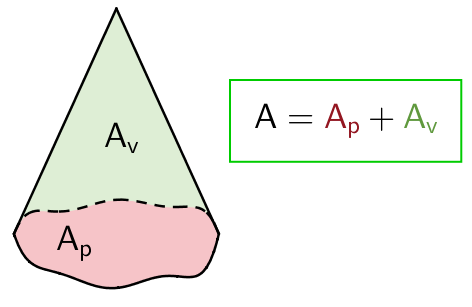
Kartiot voidaan pohja muodon perusteella luokitella samaan tapaan kuin lieriötkin. Ympyräkartion pohja on ympyrä ja monikulmiopohjaisista kartioista käytetään yleisnimitystä pyramidi. Vaipan muoto tasoon levitettynä riippuu pohjan muodosta. Ympyräkartiolla vaippa on sektorin muotoinen ja pyramidin vaippa koostuu kolmioista.
Pyramidi
Tilavuus
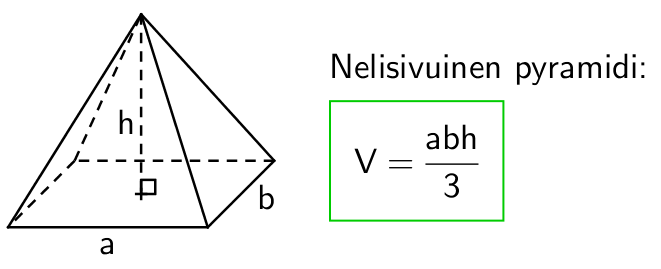
Pyramidin pohja on monikulmio. Kartion tilavuuden yleisellä kaavalla pärjää varsin hyvin, mutta malliksi on johdettu myös suorakulmio- ja neliöpohjaiselle pyramdille omat laskukaavat.
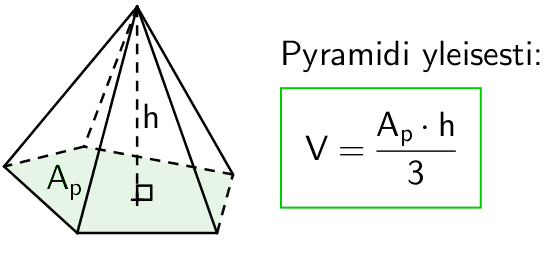
Pinta-ala
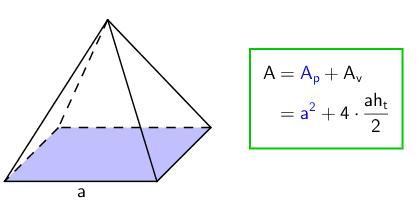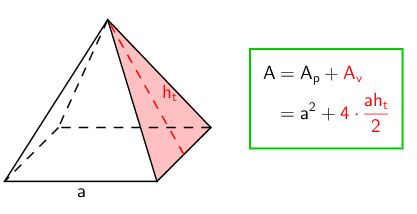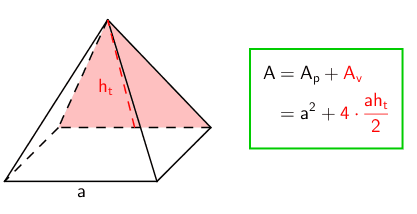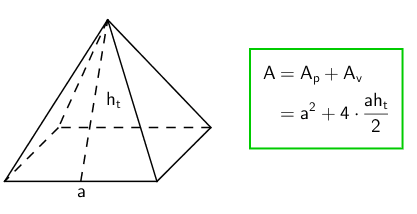
Pyramidin vaippa koostuu kolmioista, joiden lukumäärä riippuu pohjan sivujen lukumäärästä ja muoto huipun sijainnista suhteessa pohjaan. Jos pyramidi on suora, niin vaipan kolmiot ovat tasakylkisiä, mutta vinolla pyramidilla voivat kolmiot olla millaisia kolmioita tahansa. Animaatiossa on esitetty neliöpohjaisen pyramidin pinta-alan laskeminen. Huomaa, että vaipan kolmioiden (tahkojen) korkeus \(\mathsf{h_t}\) ei ole sama kuin kolmion korkeus \(\mathsf{h}\).
Ympyräkartio
Tilavuus
Ympyräkartion pohja on ympyrä, joten ympyrän pinta-alan kaavan voi sijoittaa tilavuuden laskukaavaan pohjan pinta-alan paikalle.
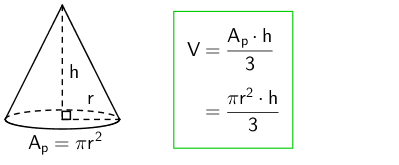
Pinta-ala
Ympyräkartion vaippa on ympyräsektori, jonka säde on ympyräkartion sivujanan pituus. Sivujana on jana, joka kulkee huipulta pohjaympyrän kehälle. Yhdistämällä ympyrän kehän pituuden sekä sektorin kaaren pituuden ja pinta-alan laskukaavat, voidaan ympyräkartion vaipan pinta-alalle johtaa melko siisti laskulauseke.

Vaipan pinta-alan laskukaavan johtaminen
Vaippa on siis sektorin muotoinen, jonka säde on kartion sivujana \(\mathsf{s}\). Keskuskulman määrittäminen kartiosta on vaikeaa, joten pyritään pääsemään siitä eroon. Käytetään hyväksi tietoa, että sektorin kaaren pituus \(\mathsf{b}\) on yhtä pitkä kuin pohjaympyrän kehän pituus \(\mathsf{p = 2\pi r}\).
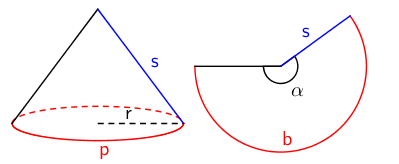
\(\require{cancel}\begin{align}\mathsf{b} &= \mathsf{p}\\ \mathsf{\dfrac{\alpha}{360^\circ} \cdot \cancel{2\pi} s} &= \mathsf{\cancel{2\pi} r} &&\mathsf{\| : s}\\ \mathsf{\dfrac{\alpha}{360^\circ}} &= \mathsf{\dfrac{r}{s}}\end{align}\)
Sijoitetaan sektorin pinta-alan laskukaavaan \(\mathsf{\dfrac{\alpha}{360^\circ}}\) paikalle edellä johdettu \(\mathsf{\dfrac{r}{s}}\) ja sievennetään lauseke.
\(\require{cancel}\begin{align}\mathsf{A_s} &= \mathsf{\dfrac{\alpha}{360^\circ} \cdot \pi s^2}\\ &= \mathsf{\dfrac{r}{\cancel{s}} \cdot \pi s^{\cancel{2}}}\\ &= \mathsf{r\pi s}\\ &= \mathsf{\pi rs}\end{align}\)
6. Pallo
Pallon tilavuuden ja pinta-alan laskemiseen tarvitaan vain pallon säde. Säteen avulla voidaan laskea myös pallon isoympyrän pituus, josta käytetään puhekielessä nimitystä ympärysmitta.